Рассмотрим автономную двумерную систему

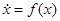,   (5)

где 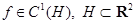 — область.

Предположим, что система (5) имеет замкнутую траекторию 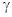 с наименьшим периодом 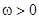. Возьмем произвольную точку  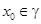и проведем через нее нормаль  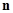к 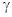 единичной длины. Для определенности считаем, что  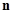направлен во внешнюю область. Не нарушая общности, считаем также, что  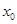— начало координат (этого можно добиться заменой 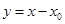). Точки на нормали  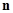определяются единственной координатой 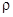. В качестве  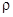берем расстояние от точки нормали до начала координат, если точка лежит снаружи 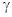, и это расстояние, взятое с обратным знаком, если она лежит внутри .

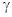Рассмотрим траектории 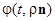, проходящие через точки нормали. Запишем уравнение

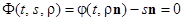(6)

с неизвестными t, s ( — параметр).

Лемма 3. Существует 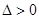 такое, что в области  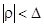уравнение (6) имеет единственное решение 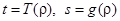, удовлетворяющее условиям 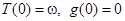, причем функции  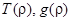непрерывно дифференцируемы при .

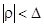Доказательство. Так как 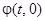 — решение с периодом , то по теореме о дифференцируемости решения функция  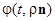определена и непрерывно дифференцируема по t и  в некоторой окрестности точки 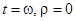. Тогда функция  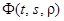определена и непрерывно дифференцируема в некоторой окрестности точки 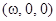. Так как  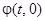‑периодична, то 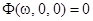. Рассмотрим якобиан  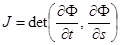в точке 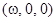. Имеем 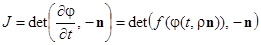. Следовательно, в точке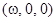 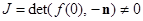, поскольку  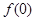и 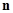 — ортогональные векторы. Тогда утверждение леммы вытекает из теоремы о неявной функции.

Следствие. Справедлива формула

.

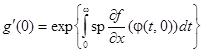Выясним геометрический смысл функций 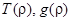. Лемма 3 утверждает, что каждая траектория, пересекающая нормаль  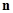в точке  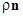из -окрестности начала координат, вновь пересечет ее через промежуток времени  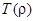в точке 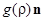. При этом так как функция  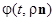также делает полный оборот вдоль  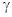при 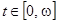, то траектория  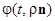также делает полный оборот при 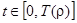, оставаясь в малой окрестности 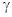, если  достаточно мало.

Функция 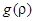 называется функцией последования.

Определение. Замкнутая траектория 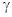 автономного уравнения (5) называется устойчивым предельным циклом, если существует такое 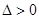, что 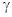 является -предельным множеством для любой траектории, проходящей через точку из -окрестности кривой .

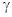Определение. Замкнутая траектория 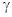 автономного уравнения (5) называется неустойчивым предельным циклом, если существует такое 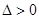, что 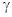 является -предельным множеством для любой траектории, проходящей через точку из -окрестности кривой .

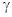Так как в реальной действительности время течет в положительном направлении, то на практике реализуются те периодические движения, которым соответствуют устойчивые предельные циклы. Такие движения называются автоколебаниями.

Теорема 4. Пусть 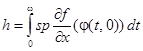. (7)

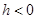Если , то 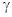 является устойчивым предельным циклом; если 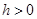, то 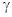 — неустойчивый предельный цикл.

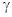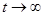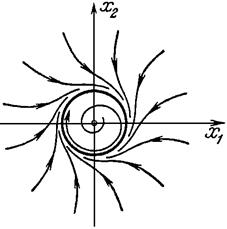
Характер приближения соседних траекторий к  при  следующий: они приближаются к 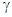, образуя бесконечное число витков спирали, как изнутри, так и снаружи.