Исследуем на устойчивость положения равновесия линейной однородной системы двух уравнений с постоянными коэффициентами. Пусть 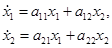 , где
, где 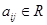 . Как было показано в пункте 1.4, тип особой точки такой системы определяется корнями характеристического уравнения
. Как было показано в пункте 1.4, тип особой точки такой системы определяется корнями характеристического уравнения 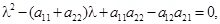 или
или 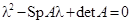 . Его корни можно найти по формуле
. Его корни можно найти по формуле
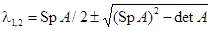 .
.
Рассмотрим следующие случаи согласно пункту 1.4.
1) 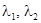 вещественны, различны и
вещественны, различны и 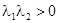 (
( 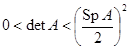 ). Параметрические уравнения траекторий:
). Параметрические уравнения траекторий: 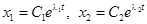 . Положение равновесия называется узел. Если корни
. Положение равновесия называется узел. Если корни 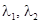 положительны (
положительны ( 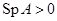 ), то решения будут неограниченно возрастать, и особая точка — неустойчивый узел.
), то решения будут неограниченно возрастать, и особая точка — неустойчивый узел.
Если 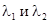 отрицательны (
отрицательны ( 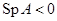 ), то решения с ростом времени будут неограниченно уменьшаться, то есть положение равновесия будет асимптотически устойчивым. Особая точка — устойчивый узел.
), то решения с ростом времени будут неограниченно уменьшаться, то есть положение равновесия будет асимптотически устойчивым. Особая точка — устойчивый узел.
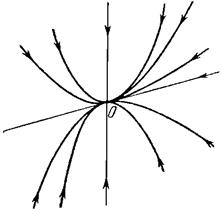
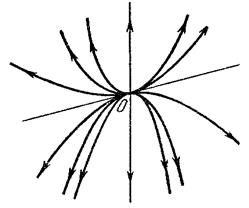
2) 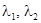 вещественны и
вещественны и 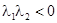 (
( 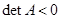 ). В этом случае одна из траекторий всегда будет неограниченно возрастать, а другая неограниченно уменьшаться. Таким образом, седло всегда неустойчиво.
). В этом случае одна из траекторий всегда будет неограниченно возрастать, а другая неограниченно уменьшаться. Таким образом, седло всегда неустойчиво.
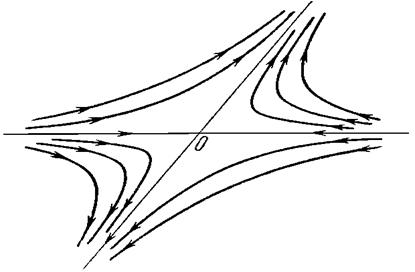
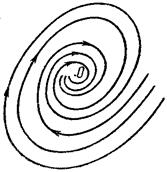
3) 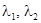 комплексно-сопряженные, но не чисто мнимые (
комплексно-сопряженные, но не чисто мнимые ( 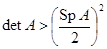 ). Решение в полярных координатах запишется в виде
). Решение в полярных координатах запишется в виде 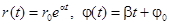 , где
, где 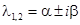 . Если
. Если 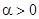 (
( 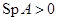 ), то спирали будут раскручиваться от особой точки, и фокус будет неустойчивым.
), то спирали будут раскручиваться от особой точки, и фокус будет неустойчивым.
Если 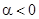 (
( 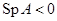 ), то особая точка — устойчивый фокус, причем устойчивость асимптотическая.
), то особая точка — устойчивый фокус, причем устойчивость асимптотическая.

4) 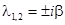 (
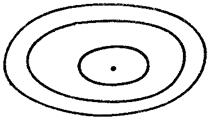
( 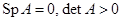 ). Особая точка — центр, траектории — окружности, то есть положение равновесия является устойчивым, но не асимптотически.
). Особая точка — центр, траектории — окружности, то есть положение равновесия является устойчивым, но не асимптотически.
5) 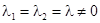 . Если
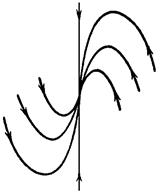
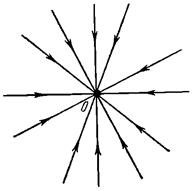
. Если 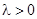 , то получаем неустойчивый узел, либо вырожденный, либо дикритический. Если
, то получаем неустойчивый узел, либо вырожденный, либо дикритический. Если 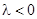 , положение равновесия будет асимптотически устойчивым.
, положение равновесия будет асимптотически устойчивым.

6) Один из корней равен нулю (например 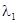 ). Траекториями являются прямые, параллельные друг другу. Если
). Траекториями являются прямые, параллельные друг другу. Если 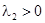 , то получаем прямую неустойчивых особых точек. Если
, то получаем прямую неустойчивых особых точек. Если 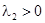 , то прямая будет содержать устойчивые особые точки.
, то прямая будет содержать устойчивые особые точки.
7) Оба корня равны нулю. Тогда 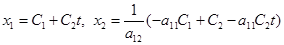 . Особая точка неустойчива.
. Особая точка неустойчива.
Пример. Рассмотрим систему 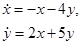 . Положение равновесия находится из уравнения
. Положение равновесия находится из уравнения 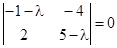 , или
, или 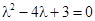 , откуда
, откуда 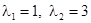 . Следовательно, положение равновесия — неустойчивый узел. Жорданова форма матрицы А имеет вид:
. Следовательно, положение равновесия — неустойчивый узел. Жорданова форма матрицы А имеет вид:
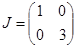 .
.
Найдем координаты преобразования 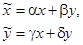 , приводящего матрицу А к жордановой форме, то есть переводящего систему к виду
, приводящего матрицу А к жордановой форме, то есть переводящего систему к виду 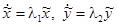 . Дифференцируя эти уравнения и подставляя в исходную систему, получаем:
. Дифференцируя эти уравнения и подставляя в исходную систему, получаем:
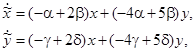
откуда с учетом 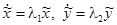
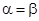 , — произвольное,
, — произвольное, 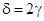 , — произвольное. Получаем преобразование
, — произвольное. Получаем преобразование 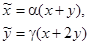 . Определим новое положение осей:
. Определим новое положение осей:
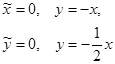
Решение системы 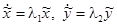 запишется в виде
запишется в виде 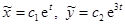 , а исходной системы отсюда
, а исходной системы отсюда 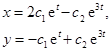 . Схематическое изображение траекторий:
. Схематическое изображение траекторий:
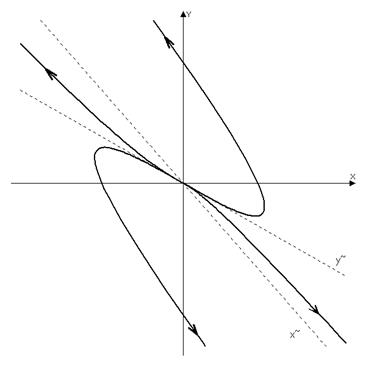
Рассмотрим теперь некоторые положения равновесия в трехмерном пространстве. Характеристическое уравнение — кубическое с вещественными коэффициентами, оно может иметь три вещественных или один вещественный и два комплексно-сопряженных корня. В зависимости от расположения этих корней 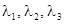 на плоскости
на плоскости 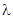 возможно 10 "грубых" случаев (рис. 3, 1)-5) и 1')-5')) и ряд "вырожденных" (рис. 3, 6)-9)), когда вещественная часть одного из корней равна нулю или вещественной части не сопряженного с ним корня. Случаи кратных корней здесь не рассматриваются.
возможно 10 "грубых" случаев (рис. 3, 1)-5) и 1')-5')) и ряд "вырожденных" (рис. 3, 6)-9)), когда вещественная часть одного из корней равна нулю или вещественной части не сопряженного с ним корня. Случаи кратных корней здесь не рассматриваются.
Поведение фазовых траекторий в приведенных случаях показано на рис. 4. Случаи 1')-5') получаются из случаев 1)-5) изменением направления оси t, так что на рис. 4 надо лишь заменить все стрелки на противоположные.
Устойчивость по Ляпунову в рассмотренных случаях следующая. Все случаи 1')-5'), а также 2), 5), 8) и 9) неустойчивы. Случаи 1), 3) и 4) устойчивы асимптотически. Случай 6) устойчив.
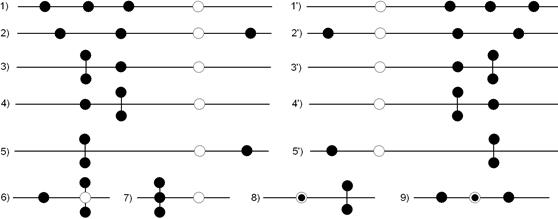
Рис. 3. Собственные числа матрицы А. Закрашенным кружком отмечены 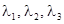 ,
,
светлым — начало координат.
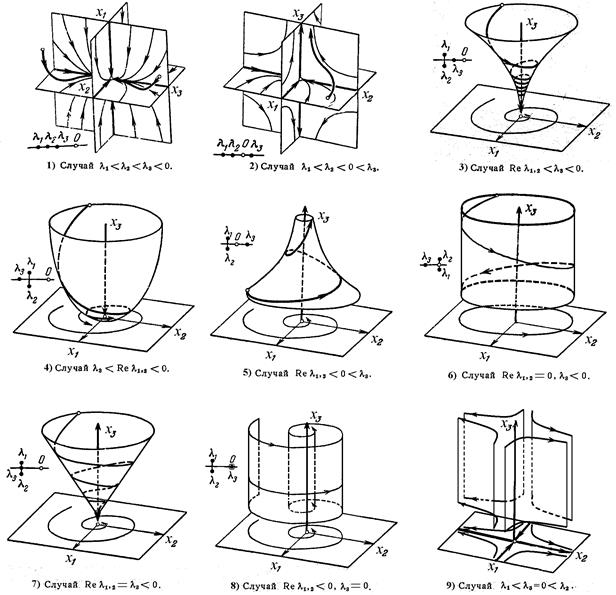
Рис. 4. Фазовые кривые в трехмерном пространстве.
Дата: 2019-05-28, просмотров: 352.