Устойчивость по Ляпунову.
Вводя определение устойчивости по Лагранжу и Пуассону в пункте 1.3, описывались свойства одной отдельно взятой траектории. Понятие устойчивости по Ляпунову характеризует траекторию с точки зрения поведения соседних траекторий, располагающихся в ее окрестности. Предположим, что система при старте из начальной точки 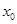 порождает траекторию
порождает траекторию 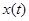 . Рассмотрим другую траекторию той же системы
. Рассмотрим другую траекторию той же системы 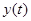 , стартовая точка которой близка к
, стартовая точка которой близка к 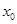 . Если обе траектории остаются близкими в любой последующий момент времени, то траектория
. Если обе траектории остаются близкими в любой последующий момент времени, то траектория 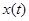 называется устойчивой по Ляпунову.
называется устойчивой по Ляпунову.
Наглядная иллюстрация устойчивости по Лагранжу, Пуассону и Ляпунову приводится на рис. 2. Когда говорят просто об устойчивой траектории, то всегда имеется в виду устойчивость по Ляпунову.
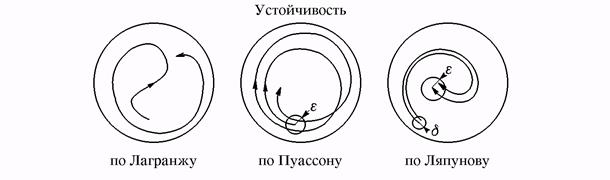
Рис. 2. Качественная иллюстрация устойчивости по Лагранжу (траектория остается в замкнутой области), по Пуассону (траектория многократно возвращается в -окрестность стартовой точки) и по Ляпунову (две близкие на старте траектории остаются близкими всегда)
Рассмотрим уравнение 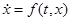 (1)
(1)
где 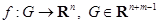 и функция f удовлетворяет в G условию Липшица локально:
и функция f удовлетворяет в G условию Липшица локально:
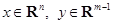 и
и 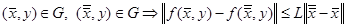 , где
, где 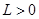 — константа, не зависящая от выбора точек
— константа, не зависящая от выбора точек 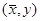 и
и 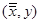 .
.
Предположим, что уравнение (1) имеет решение 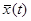 , определенное при
, определенное при 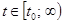 , и что
, и что 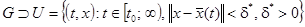 . Чтобы перейти к исследованию нулевого решения, выполним в (1) замену
. Чтобы перейти к исследованию нулевого решения, выполним в (1) замену 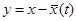 . В результате получим уравнение
. В результате получим уравнение
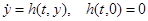 , (2)
, (2)
где 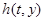 определена в области, содержащей множество
определена в области, содержащей множество 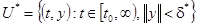 . Это уравнение называется уравнением в отклонениях. Пусть
. Это уравнение называется уравнением в отклонениях. Пусть 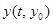 — решение (2) с начальными данными
— решение (2) с начальными данными 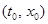 .
.
Определение. Решение 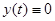 уравнения (2) называется устойчивым по Ляпунову, если для
уравнения (2) называется устойчивым по Ляпунову, если для 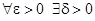 , такое, что при
, такое, что при 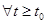
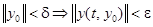 .
.
Решение 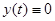 называется асимптотически устойчивым, если оно устойчиво по Ляпунову и существует
называется асимптотически устойчивым, если оно устойчиво по Ляпунову и существует 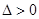 такое, что
такое, что 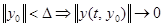 при
при 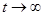 .
.
Неустойчивость решения 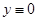 означает следующее: существуют положительное
означает следующее: существуют положительное 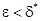 , последовательность начальных точек
, последовательность начальных точек 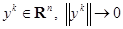 при
при 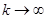 , и последовательность моментов времени
, и последовательность моментов времени 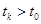 такие, что
такие, что 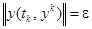 .
.
При исследовании вопроса об устойчивости решений часто прибегают к заменам переменных, позволяющим упростить вид рассматриваемого уравнения. Сделаем в (2) замену 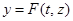 , где функция
, где функция 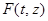 определена при всех
определена при всех 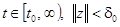 и непрерывна по z при
и непрерывна по z при 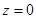 равномерно относительно
равномерно относительно 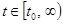 , причем
, причем 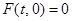 . Пусть уравнение
. Пусть уравнение 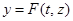 однозначно разрешимо относительно z:
однозначно разрешимо относительно z: 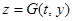 , где
, где 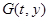 определена на множестве
определена на множестве 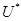 и непрерывна по y при
и непрерывна по y при 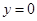 равномерно относительно
равномерно относительно 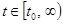 . Пусть уравнение (2) заменой
. Пусть уравнение (2) заменой 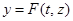 можно преобразовать в уравнение
можно преобразовать в уравнение 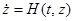 .
.
Лемма. При сделанных предположениях нулевое решение уравнения (2) устойчиво по Ляпунову, асимптотически устойчиво или неустойчиво тогда и только тогда, когда соответственно устойчиво по Ляпунову, асимптотически устойчиво или неустойчиво нулевое решение уравнения 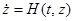 .
.
Пусть уравнение (2) автономно, а его нулевое решение асимптотически устойчиво. Множество 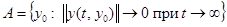 называется областью притяжения решения
называется областью притяжения решения 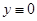 .
.
Дата: 2019-05-28, просмотров: 367.