Рассмотрим многоканальную СМО с ожиданием и неограниченной длиной очереди, на которую поступает поток заявок с интенсивностью 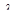 и которая имеет интенсивность обслуживания каждого канала 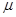. Размеченный граф состояний представлен на рис 3.7 Он имеет бесконечное число состояний:

S 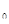- все каналы свободны, k=0;

S 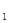- занят один канал, остальные свободны, k=1;

S - заняты два канала, остальные свободны, k=2;

S - заняты все n каналов, k=n, очереди нет;

S 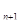- заняты все n каналов, одна заявка в очереди, k=n+1,

S 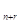- заняты все n каналов, r заявок в очереди, k=n+r,

Вероятности состояний получим из формул для многоканальной СМО с ограниченной очередью при переходе к пределу при m 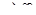. Следует заметить, что сумма геометрической прогрессии в выражении для p 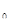расходится при уровне загрузки p/n>1, очередь будет бесконечно возрастать, а при p/n<1 ряд сходится, что определяет установившийся стационарный режим работы СМО.

Очереди нет

…

…

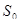
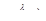
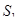
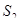
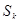
Рис.3.7 Размеченный граф состояний многоканальной СМО

с неограниченной очередью

для которого и определим выражения для предельных вероятностей состояний:

 …;

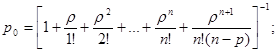
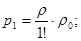
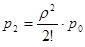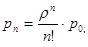
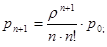
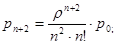
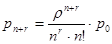
Поскольку отказа в обслуживании в таких системах не может быть, то характеристики пропускной способности равны:

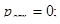
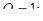
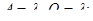
среднее число заявок в очереди –

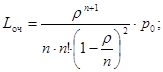
среднее время ожидания в очереди –

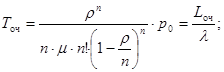
среднее число заявок в СМО –

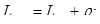
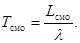
Вероятность того, что СМО находится в состоянии , когда нет заявок и не занято ни одного канала, определяется выражением

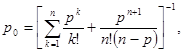
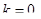
Эта вероятность определяет среднюю долю времени простоя канала обслуживания. Вероятность занятости обслуживанием k заявок –

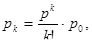
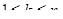
На этом основании можно определить вероятность, или долю времени занятости всех каналов обслуживанием

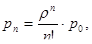
Если же все каналы уже заняты обслуживанием, то вероятность состояния определяется выражением

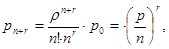
Вероятность оказаться в очереди равна вероятности застать все каналы уже занятыми обслуживанием

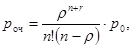
Среднее число заявок, находящихся в очереди и ожидающих обслуживания, равно:

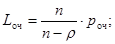
Среднее время ожидания заявки в очереди по формуле Литтла: 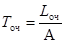 и в системе

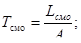
среднее число занятых каналов обслуживанием:

;

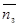
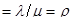среднее число свободных каналов:

;

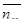
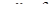коэффициент занятости каналов обслуживанием:

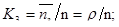
Важно заметить, что параметр характеризует степень согласования входного потока, например покупателей в магазине с интенсивностью потока обслуживания. Процесс обслуживания будет стабилен при Если же 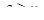в системе будут возрастать средняя длина очереди и среднее время ожидания покупателями начала обслуживания и, следовательно, СМО будет работать неустойчиво.