Проведем анализ простой одноканальной СМО с отказами в обслуживании, на которую поступает пуассоновский поток заявок с интенсивностью λ, а обслуживание происходит под действием пуассоновского потока с интенсивностью μ.

Работу одноканальной СМО n=1 можно представить в виде размеченного графа состояний (3.1).

Переходы СМО из одного состояния S₀ в другое S₁ происходят под действием входного потока заявок с интенсивностью λ, а обратный переход – под действием потока обслуживания с интенсивностью μ.

 λ

S0

 μ

S₀ – канал обслуживания свободен; S₁ – канал занят обслуживанием;

Рис. 3.1 Размеченный граф состояний одноканальной СМО

Запишем систему дифференциальных уравнений Колмогорова для вероятностей состояния по изложенным выше правилам:

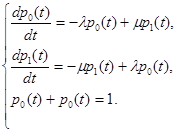
Откуда получим дифференциальное уравнение для определения вероятности р₀(t) состояния S₀:

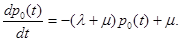
Это уравнение можно решить при начальных условиях в предположении, что система в момент t=0 находилась в состоянии S₀, тогда р₀(0)=1, р₁(0)=0.

В этом случае решение дифференциального уровнения позволяет определить вероятность того, что канал свободен и не занят обслуживанием:

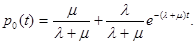
Тогда нетрудно получить выражение для вероятности определения вероятности занятости канала:

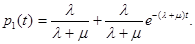
Вероятность р₀(t) уменьшается с течением времени и в пределе при t→∞ стремится к величине

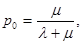
а вероятность р₁(t) в то же время увеличивается от 0, стремясь в пределе при t→∞ к величине

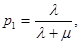
Эти пределы вероятностей могут быть получены непосредственно из уравнений Колмогорова при условии

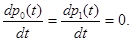
Функции р₀(t) и р₁(t) определяют переходный процесс в одноканальной СМО и описывают процесс экспоненциального приближения СМО к своему предельному состоянию с постоянной времени 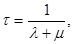 характерной для рассматриваемой системы.

С достаточной для практики точностью можно считать, что переходный процесс в СМО заканчивается в течение времени, равно 3τ.

Вероятность р₀(t) определяет относительную пропускную способность СМО, которая определяет долю обслуживаемых заявок по отношению к полному числу поступающих заявок, в единицу времени.

Действительно, р₀(t) есть вероятность того, что заявка, пришедшая в момент t, будет принята к обслуживанию. Всего в единицу времени приходит в среднем λ заявок и из них обслуживается λр₀ заявок.

Тогда доля обслуживаемых заявок по отношению ко всему потоку заявок определятся величиной

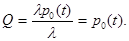
В пределе при t→∞ практически уже при t>3τ значение относительной пропускной способности будет равно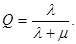

Абсолютная пропускная способность, определяющая число заявок, обслуживаемых в единицу времени в пределе при t→∞, равна:

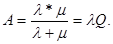
Соответственно доля заявок, получивших отказ, составляет в этих же предельных условиях:

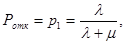
а общее число не обслуженных заявок равно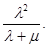

Примерами одноканальных СМО с отказами в обслуживании являются: стол заказов в магазине, диспетчерская автотранспортного предприятия, контора склада, офис управления коммерческой фирмы, с которыми устанавливается связь по телефону.