В коммерческой деятельности в качестве одноканальной СМО с неограниченным ожиданием является, например, коммерческий директор, поскольку он, как правило, вынужден выполнять обслуживание заявок различной природы: документы, переговоры по телефону, встречи и беседы с подчиненными, представителями налоговой инспекции, милиции, товароведами, маркетологами, поставщиками продукции и решать задачи в товарно-финансовой сфере с высокой степенью финансовой ответственности, что связано с обязательным выполнением запросов, которые ожидают иногда нетерпеливо выполнения своих требований, а ошибки неправильного обслуживания, как правило, экономически весьма ощутимы.
В то же время товары, завезенные для продажи (обслуживания), находясь на складе, образуют очередь на обслуживание (продажу).
Длину очереди составляет количество товаров, предназначенных для продажи. В этой ситуации продавцы выступают в роли каналов, обслуживающих товары. Если количество товаров, предназначенных для продажи, велико, то в этом случае мы имеем дело с типичным случаем СМО с ожиданием.
Рассмотрим простейшую одноканальную СМО с ожиданием обслуживания, на которую поступает пуассоновский поток заявок с интенсивностью λ и интенсивностью обслуживания µ.
Причем заявка, поступившая в момент, когда канал занят обслуживанием, ставится в очередь и ожидает обслуживания.
Размеченный граф состояний такой системы приведен на рис. 3.5
Количество возможных состояний ее бесконечно:
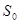 - канал свободен, очереди нет,
- канал свободен, очереди нет, 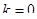 ;
;
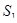 - канал занят обслуживанием, очереди нет,
- канал занят обслуживанием, очереди нет, 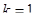 ;
;
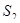 - канал занят, одна заявка в очереди,
- канал занят, одна заявка в очереди, 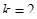 ;
;
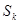 - канал занят
- канал занят 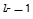 , заявка в очереди.
, заявка в очереди.
Модели оценки вероятности состояний СМО с неограниченной очередью можно получить из формул, выделенных для СМО с неограниченной очередью, путем перехода к пределу при m→∞:
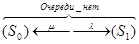
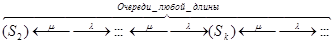
Рис. 3.5 Граф состояний одноканальной СМО с неограниченной очередью.
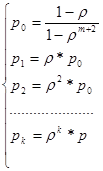
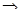
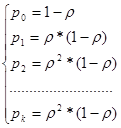
Следует заметить, что для СМО с ограниченной длиной очереди в формуле
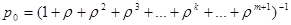
имеет место геометрическая прогрессия с первым членом 1 и знаменателем 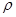 . Такая последовательность представляет собой сумму бесконечного числа членов при
. Такая последовательность представляет собой сумму бесконечного числа членов при 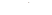 . Эта сумма сходится, если прогрессия, бесконечно убывающая при
. Эта сумма сходится, если прогрессия, бесконечно убывающая при 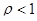 , что определяет установившийся режим работы СМО, с при
, что определяет установившийся режим работы СМО, с при 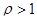 очередь при
очередь при 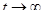 с течением времени может расти до бесконечности.
с течением времени может расти до бесконечности.
Поскольку в рассматриваемой СМО ограничение на длину очереди отсутствует, то любая заявка может быть обслужена, поэтому 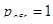 , следовательно, относительная пропускная способность
, следовательно, относительная пропускная способность 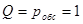 , соответственно
, соответственно 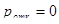 , а абсолютная пропускная способность
, а абсолютная пропускная способность
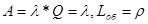 .
.
Вероятность пребывания в очереди k заявок равна:
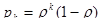 ;
;
Среднее число заявок в очереди –
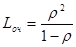 ;
;
Среднее число заявок в системе –
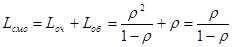 ;
;
Среднее время пребывания заявки в системе –
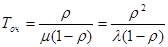 ;
;
Среднее время пребывания заявки с системе –
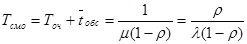 .
.
Если в одноканальной СМО с ожиданием интенсивность поступления заявок больше интенсивности обслуживания 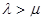 , то очередь будет постоянно увеличиваться. В связи с этим наибольший интерес представляет анализ устойчивых СМО, работающих в стационарном режиме при
, то очередь будет постоянно увеличиваться. В связи с этим наибольший интерес представляет анализ устойчивых СМО, работающих в стационарном режиме при 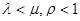 .
.
Дата: 2019-05-28, просмотров: 320.