Рассмотрим многоканальную СМО 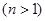 , на вход которой поступает пуассоновский поток заявок с интенсивностью
, на вход которой поступает пуассоновский поток заявок с интенсивностью 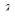 , а интенсивность обслуживания каждого канала составляет
, а интенсивность обслуживания каждого канала составляет 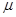 , максимально возможное число мест в очереди ограничено величиной m. Дискретные состояния СМО определяются количеством заявок, поступивших в систему, которые можно записать.
, максимально возможное число мест в очереди ограничено величиной m. Дискретные состояния СМО определяются количеством заявок, поступивших в систему, которые можно записать.
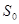 - все каналы свободны,
- все каналы свободны, 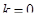 ;
;
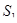 - занят только один канал (любой),
- занят только один канал (любой), 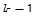 ;
;
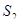 - заняты только два канала (любых),
- заняты только два канала (любых), 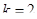 ;
;
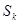 - заняты все
- заняты все 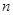 каналов,
каналов, 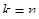 .
.
Пока СМО находится в любом из этих состояний, очереди нет. После того как заняты все каналы обслуживания, последующие заявки образуют очередь, тем самым, определяя дальнейшие состояние системы:
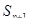 - заняты все
- заняты все 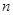 каналов и одна заявка стоит в очереди,
каналов и одна заявка стоит в очереди,
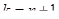 ;
;
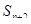 - заняты все
- заняты все 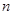 каналов и две заявки стоят в очереди,
каналов и две заявки стоят в очереди,
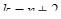 ;
;
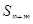 - заняты все
- заняты все 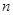 каналов и все
каналов и все 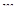 мест в очереди,
мест в очереди,
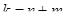 .
.
Граф состояний n-канальной СМО с очередью, ограниченной m местами на рис.3.6
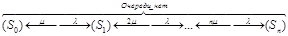
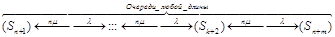
Рис. 3.6 Граф состояний n-канальной СМО с ограничением на длину очереди m
Переход СМО в состояние с большими номерами определяется потоком поступающих заявок с интенсивностью 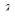 , тогда как по условию в обслуживании этих заявок принимают участие
, тогда как по условию в обслуживании этих заявок принимают участие 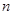 одинаковых каналов с интенсивностью потока обслуживания равного
одинаковых каналов с интенсивностью потока обслуживания равного 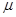 для каждого канала. При этом полная интенсивность потока обслуживания возрастает с подключением новых каналов вплоть до такого состояния
для каждого канала. При этом полная интенсивность потока обслуживания возрастает с подключением новых каналов вплоть до такого состояния 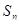 , когда все n каналов окажутся занятыми. С появлением очереди интенсивность обслуживания более увеличивается, так как она уже достигла максимального значения, равного
, когда все n каналов окажутся занятыми. С появлением очереди интенсивность обслуживания более увеличивается, так как она уже достигла максимального значения, равного 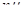 .
.
Запишем выражения для предельных вероятностей состояний:
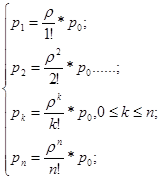
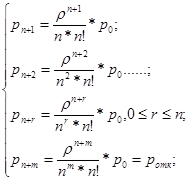
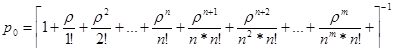 .
.
Выражение для 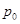 можно преобразовать, используя формулу геометрической прогрессии для суммы членов со знаменателем
можно преобразовать, используя формулу геометрической прогрессии для суммы членов со знаменателем 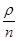 :
:
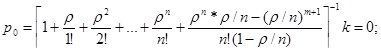
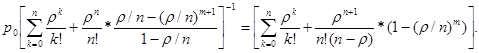
Образование очереди возможно, когда вновь поступившая заявка застанет в системе не менее 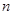 требований, т.е. когда в системе будет находиться
требований, т.е. когда в системе будет находиться 
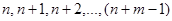 требований. Эти события независимы, поэтому вероятность того, что все каналы заняты, равна сумме соответствующих вероятностей
требований. Эти события независимы, поэтому вероятность того, что все каналы заняты, равна сумме соответствующих вероятностей 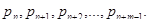 Поэтому вероятность образования очереди равна:
Поэтому вероятность образования очереди равна:
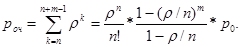
Вероятность отказа в обслуживании наступает тогда, когда все 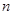 каналов и все
каналов и все  мест в очереди заняты:
мест в очереди заняты:
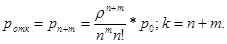
Относительная пропускная способность будет равна:
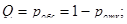
Абсолютная пропускная способность –
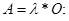
Среднее число занятых каналов –
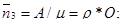
Среднее число простаивающих каналов –
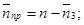
Коэффициент занятости (использования) каналов –
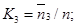
Коэффициент простоя каналов –
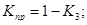
Среднее число заявок, находящихся в очередях –
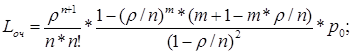
В случае если 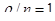 , эта формула принимает другой вид –
, эта формула принимает другой вид –
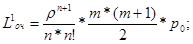
Среднее время ожидания в очереди определяется формулами Литтла –
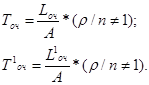
Среднее время пребывания заявки в СМО, как и для одноканальной СМО, больше среднего времени ожидания в очереди на среднее время обслуживания, равное 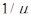 , поскольку заявка всегда обслуживается только одним каналом:
, поскольку заявка всегда обслуживается только одним каналом:
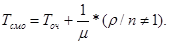
Дата: 2019-05-28, просмотров: 344.