Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

В коммерческой деятельности чаще встречаются СМО с ожиданием (очередью).

Рассмотрим простую одноканальную СМО с ограниченной очередью, в которой число мест в очереди т - фиксированная величина. Следовательно, заявка, поступившая в тот момент, когда все места в очереди заняты, не принимается к обслуживанию, не встает в очередь и .покидает систему.

Граф этой СМО представлен на рис. 3.4 и совпадает с графом рис. 2.1 описывающим процесс «рождения—гибели», с тем отличием, что при наличии только одного канала.

 

Sm

S3

S2

S1

S0

 λ λ λ λ ... λ

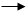
 μ μ μ μ ... μ

 

Рис. 3.4. Размеченный граф процесса «рождения - гибели» обслуживания все интенсивности потоков обслуживания равны

 

Состояния СМО можно представить следующим образом:

S₀ - канал обслуживания свободен,

S, - канал обслуживания занят, но очереди нет,

S₂ - канал обслуживания занят, в очереди стоит одна заявка,

S₃ - канал обслуживания занят, в очереди стоят две заявки,

S_m+1 - канал обслуживания занят, в очереди все т мест заняты, любая следующая заявка получает отказ.

Для описания случайного процесса СМО можно воспользоваться изложенными ранее правилами и формулами. Напишем выражения, определяющие предельные вероятности состояний:

 

p₁ = ρ * ρ_о

p₂=ρ^{2 *} ρ₀

p_k=ρ^k * ρ₀

P_m+1 = p^m=1 * ρ₀

p₀=[1+ρ+ρ²+ρ³+...+ρ^m+1]^-1

Выражение для р₀ можно в аанном случае записать проще, пользуясь тем, что в знаменателе стоит геометрическая прогрессия относительно р, тогда после соответствующих преобразований получаем:

 

ρ= (1- ρ )

(1- ρ^m+2)

 

Эта формула справедлива для всех р, отличных от 1, если же р = 1, то р₀ = 1/(т + 2), а все остальные вероятности также равны 1/(т + 2). Если предположить т = 0, то мы переходим от рассмотрения одноканальной СМО с ожиданием к уже рассмотренной одноканальной СМО с отказами в обслуживании. Действительно, выражение для предельной вероятности р₀ в случае т = 0 имеет вид:

 

p_о ⁼ μ / (λ+μ)

 

И в случае λ ⁼ μ имеет величину р₀ = 1 / 2.

Определим основные характеристики одноканальной СМО с ожиданием: относительную и абсолютную пропускную способность, вероятность отказа, а также среднюю длину очереди и среднее время ожидания заявки в очереди.

Заявка получает отказ, если она поступает в момент времени, когда СМО уже находится в состоянии S_m+1 и, следовательно, все места в очереди да заняты и один канал обслуживает Поэтому вероятность отказа определяется вероятностью появлением

Состояния S_m+1:

 

P_отк = p_m+1 = ρ^m+1 * p₀

 

Относительная пропускная способность, или доля обслуживаемых заявок, поступающих в единицу времени, определяется выражением

 

Q = 1- p_отк = 1- ρ^m+1 * p₀

 

абсолютная пропускная способность равна:

 

A = Q * λ

 

Среднее число заявок L_оч стоящих в очереди на обслуживание, определяется математическим ожиданием случайной величины к - числа заявок, стоящих в очереди

 

L_оч-= M(k).

 

случайная величина к принимает следующие только целочисленные значения:

1 - в очереди стоит одна заявка,

2 - в очереди две заявки,

т-в очереди все места заняты

 

Вероятности этих значений определяются соответствующими вероятностями состояний, начиная с состояния S₂. Закон распределения дискретной случайной величины к изображается следующим образом:

 

k	1	2		m
pi	p2	p3		pm+1

 

Математическое ожидание этой случайной величины равно:

 

L_оч = 1* p₂ +2* p₃ +...+ m* p_m+1

В общем случае при p ≠1 эту сумму можно преобразовать, пользуясь моделями геометрической прогрессии, к более удобному виду:

 

L_оч = p² * 1- p^m * (m-m*p+1) _* p₀

( 1- p )²

 

В частном случае при р = 1, когда все вероятности p_k оказываются равными, можно воспользоваться выражением для суммы членов числового ряда

 

1+2+3+ m = m ( m +1)

2

 

Тогда получим формулу

 

L’_оч = m(m+1) _* p₀ = m(m+1) (p=1).

2 2(m+1)

 

Применяя аналогичные рассуждения и преобразования, можно показать, что среднее время ожидания обслуживания за явки а очереди определяется формулами Литтла

 

Т_оч = L_оч/А (при р ≠ 1) и Т¹_оч = L’_оч /А(при р = 1).

 

Такой результат, когда оказывается, что Т_оч ~ 1/ λ, может показаться странным: с увеличением интенсивности потока заявок как будто бы должна возрастать длина очереди и уменьшается среднее время ожидания. Однако следует иметь в виду, что, во-первых, величина L_оч является функцией от λ и μ и, во-вторых, рассматриваемая СМО имеет ограниченную длину очереди не более m заявок.

Заявка, поступившая в СМО в момент времени, когда все каналы заняты, получает отказ, и, следовательно, время ее «ожидания» в СМО равно нулю. Это приводит в общем случае (при р ≠ 1) к уменьшению Т_оч ростом λ, поскольку доля таких заявок с ростом λ увеличивается.

Если отказаться от ограничения на длину очереди, т.е. устремить m —> →∞, то случаи р < 1 и р ≥1 начинают существенно различаться. Записанные выше формулы для вероятностей состояний преобразуются в случае р < 1 к виду

 

р₀=1-р

р₁ =р*(1-р)

p₂=p²(1-p)

p_k=р^k *(1 - р)

 

При достаточно большом к вероятность p_k стремится к нулю. Поэтому относительная пропускная способность будет Q = 1, а абсолютная пропускная способность станет равной А —λ Q — λ следовательно, обслуживаются все поступившие заявки, причем средняя длина очереди окажется равной:

 

L_оч = p ² 1-p

 

а среднее время ожидания по формуле Литтла

 

Т_оч = L_оч/А

 

В пределе р << 1 получаем Т_оч = ρ / μ т.е. среднее время ожидания быстро уменьшается с увеличением интенсивности потока обслуживания. В противном случае при р ≥ 1 оказывается, что в СМО отсутствует установившийся режим. Обслуживание не успевает за потоком заявок, и очередь неограниченно растет со временем (при t → ∞). Предельные вероятности состояний поэтому не могут быть определены: при Q = 1 они равны нулю. Фактически СМО не выполняет своих функций, поскольку она не в состоянии обслужить все поступающие заявки. Нетрудно определить, что доля обслуживаемых заявок и абсолютная пропускная способность соответственно составляют в среднем ρ и μ, однако неограниченное увеличение очереди, а следовательно, и времени ожидания в ней приводит к тому, что через некоторое время заявки начинают накапливаться в очереди на неограниченно долгое время.

В качестве одной из характеристик СМО используют среднее время Т_смо пребывания заявки в СМО, включающее среднее время пребывания в очереди и среднее время обслуживания. Эта величина вычисляется по формулам Литтла: если длина очереди ограничена — среднее число заявок, находящихся в очереди, равно:

 

L_смо= m +1 ;2

Т_смо= L смо; при p ≠1

 

A тогда среднее время пребывания заявки в системе массового обслуживания (как в очереди, так и под обслуживанием) равно:

 

Т_смо= m +1 при p ≠1 2μ