Простейшие механические колебательные системы:
Линейный осциллятор,
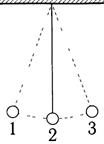
Физический маятник,
Математический маятник,
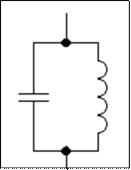
Колебательный контур
1) Линейный гармонический осциллятор - материальная точка массы m, совершающая гармонические колебания под действием упругой силы 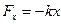 .
.
Примером такой системы может служить пружинный маятник.
Дифференциальное уравнение движения:
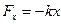 , но
, но 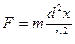
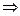
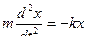
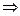
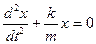
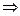
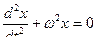 , где
, где 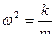 .
.
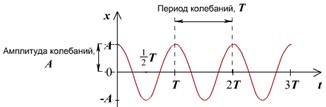
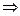 осциллятор (пружинный маятник) совершает гармонические колебания по закону x = А sin(wt+j0) с циклической частотой и периодом, равными:
осциллятор (пружинный маятник) совершает гармонические колебания по закону x = А sin(wt+j0) с циклической частотой и периодом, равными:
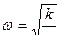 ,
, 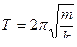 .
.
Решением уравнения 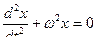 является зависимость
является зависимость
x = А cos(wt+j0) или x = А sin(wt+j0)
| |
|
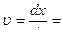
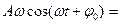
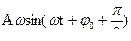 ;
;
 .
.
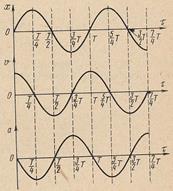
Скорость изменяется с той же частотой, опережая по фазе на 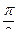 .
.
Ускорение колеблющейся точки – вторая производная уравнения колебаний:
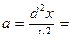

 ;
;
 .
.
Ускорение изменяется с той же частотой, что и координата, опережая по фазе на 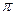 .
.
Кинетическая энергия материальной точки, совершающей гармонические колебания, равна:
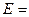
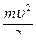 =
= 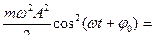
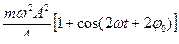 , т.к.
, т.к. 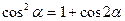 .
.
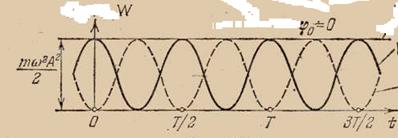
Кинетическая энергия материальной точки периодически изменяется от 0 до 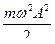 , совершая гармонические колебания с циклической частотой 2ω и амплитудой
, совершая гармонические колебания с циклической частотой 2ω и амплитудой 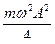 около среднего значения, равного
около среднего значения, равного 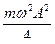 .
.
Потенциальная энергия материальной точки, гармонически колеблющейся под действием возвращающей силы, равна
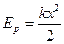 =
= 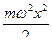 =
= 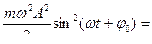
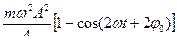 =
=
= 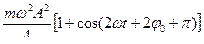 , т.к.
, т.к. 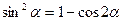
Потенциальная энергия материальной точки периодически изменяется от 0 до 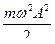 , совершая гармонические колебания с циклической частотой 2ω и амплитудой
, совершая гармонические колебания с циклической частотой 2ω и амплитудой 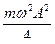 около среднего значения, равного
около среднего значения, равного 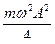 .
.
|
|
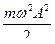 .
.
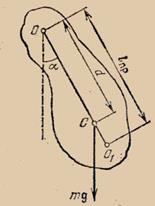
2) Физический маятник - твердое тело, имеющее возможность качаться под действием его силы тяжести mg вокруг неподвижной горизонтальной оси О, не проходящей через центр тяжести тела и называемой осью качания маятника, отклоняющиеся на углы не более 5-7º.
Центр тяжести маятника совпадает с его центром инерции С.
В отсутствие сил трения в системе уравнение движения маятника имеет вид:  ,
, 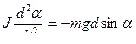 .
.
При малых колебаниях маятника sina=a, 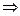 ,дифференциальное уравнение движения маятника имеет вид:
,дифференциальное уравнение движения маятника имеет вид:

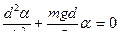 ,
, 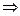 ,
, 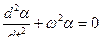 , где
, где 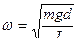 , и,
, и, 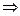 ,
,  .
.
|
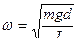 ,
,  .
.
3) Математический маятник - материальная точка, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости под действием силы тяжести.
Математический маятник представляет собой предельный случай физического маятника, вся масса которого сосредоточена в его центре инерции, так что d = l - длина математического маятника. Момент инерции такого маятника относительно оси качания J = ml 2 . Соответственно, циклическая частота и период малых колебаний математического маятника равны: 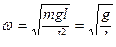 .
.
Значит, 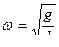 ,
, 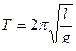 .
.
|
Согласно правилу Кирхгофа падение напряжения на конденсаторе равно электродвижущей силе в катушке индуктивности:
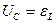 .
.
Напряжение на конденсаторе пропорционально заряду на его обкладках:
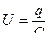 , а электродвижущая сила в катушке определяется формулой
, а электродвижущая сила в катушке определяется формулой 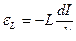 .
.
Следовательно, получим равенство
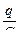 =
= 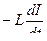 или
или 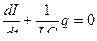 , из которого получим дифференциальное уравнение для заряда: учитывая, что
, из которого получим дифференциальное уравнение для заряда: учитывая, что 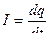
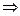
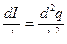 .
.
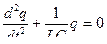 или
или 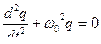 , где
, где 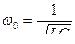 - собственная частота электромагнитных колебаний.
- собственная частота электромагнитных колебаний.
Решением этого уравнения является зависимость  , которая описывает гармонические колебания заряда на обкладках конденсатора.
, которая описывает гармонические колебания заряда на обкладках конденсатора.
В колебательном контуре рассматривается энергия электрического поля в заряженном конденсаторе ( 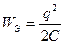 ) и энергия магнитного поля в катушке (
) и энергия магнитного поля в катушке ( 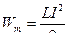 ).
).
Дата: 2019-04-23, просмотров: 314.