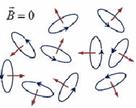|
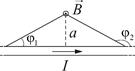
Опыт Эрстеда (1820 г.). Эрстед поместил над магнитной стрелкой прямолинейный провод, параллельный стрелке. Стрелка могла свободно вращаться вокруг вертикальной оси. При пропускании по проводу электрического тока стрелка отклонялась в сторону и устанавливалась перпендикулярно к проводу.
Таким образом, была установлена связь между электрическими и магнитными явлениями.
Источником магнитного поля является движущаяся заряженная частица.
Магнитное поле создается проводниками с током, движущимися электрически заряженными частицами и телами, частицами и телами, обладающими магнитными моментами, а также изменяющимся во времени электрическим полем.
Магнитное поле действует только на движущиеся электрически заряженные частицы и тела, на проводники с током и на частицы и тела, обладающие магнитными моментами.
Магнитная индукция - силовая характеристика магнитного поля, векторная величина, обозначается 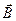 .
.
Вектор магнитной индукции можно ввести одним из трех эквивалентных способов:
- основываясь на силовом действии магнитного поля на малый элемент проводника с током (через действие силы Ампера);
- исходя из силового действия магнитного поля на движущуюся в нем заряженную частицу - точечный электрический заряд (через действие силы Лоренца);
|
Единица магнитной индукции [Тл] (тесла).
|
Линии магнитной индукции нигде не обрываются, т. е. не начинаются и не кончаются. Они либо замкнуты, либо идут из бесконечности в бесконечность.
Магнитное поле называется однородным, если во всех его точках вектор магнитной индукции имеет одно и то же значение.

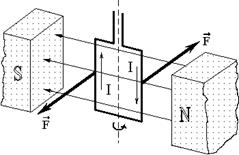
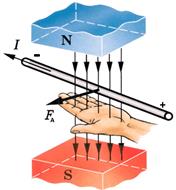
Сила Ампера
– сила, действующая на проводники с электрическим током, находящиеся во внешнем магнитном поле 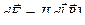 ,
, 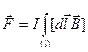 , если поле однородно, а проводник прямолинейный, то модуль силы Ампера равен
, если поле однородно, а проводник прямолинейный, то модуль силы Ампера равен

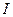 – сила тока, [А];
– сила тока, [А];
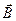 - магнитная индукция, [Тл];
- магнитная индукция, [Тл];
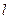 - длина проводника, [м];
- длина проводника, [м];
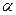 - угол между направлением тока (вектором плотности тока) в проводнике и вектором магнитной индукции внешнего магнитного поля.
- угол между направлением тока (вектором плотности тока) в проводнике и вектором магнитной индукции внешнего магнитного поля.
Следовательно, зная значения силы тока, длины проводника и силы Ампера можно экспериментально установить величину магнитной индукции внешнего поля:
|
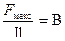 .
.
Но магнитная индукция не зависит, ни от силы тока, ни от длины проводника – это силовая характеристика внешнего магнитного поля.
Направление максимальной силы Ампера определяется правилом левой руки:
1.Линии магнитного поля входят в ладонь.
2.Четыре пальца направлены по току.
3.Большой палец указывает направление силы Ампера.
|
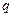 , движущуюся во внешнем магнитном поле индукции
, движущуюся во внешнем магнитном поле индукции 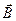 со скоростью
со скоростью 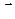 .
.
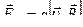
Модуль силы Лоренца равен 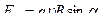 ,
,
q – заряд, [Кл];
 - скорость, [м/с];
- скорость, [м/с];
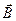 - магнитная индукция, [Тл].
- магнитная индукция, [Тл].
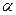 - угол между векторами
- угол между векторами 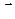 и
и 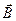 .
.
Следовательно, зная значения скорости заряженной частицы, величины заряда частицы и силы Лоренца можно экспериментально установить величину магнитной индукции внешнего поля:
|
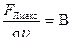 .
.
Но магнитная индукция не зависит, ни от заряда и скорости частицы – это силовая характеристика внешнего магнитного поля.
Направление силы Лоренца определяется также правилом левой руки:
1.Линии магнитного поля входят в ладонь.
2.Четыре пальца направлены по скорости движения положительно заряженной частицы.
3.Большой палец указывает направление силы Лоренца.
|
Максимальная сила Лоренца направлена всегда перпендикулярно к скорости заряженной частицы и сообщает ей нормальное ускорение (частица движется по окружности), следовательно, сила Лоренца не совершает работы. Поэтому кинетическая энергия заряженной частицы при движении частицы в магнитном поле не изменяется.
|
Произвольный плоский контур с током, находится в однородном магнитном поле.
Силы Ампера, приложенные к противоположным элементам контура, образуют пару.
Магнитным моментом контура с током называется величина равная произведению:
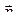 =
= 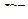 .
.
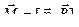
Вращающий момент максимален, если контур так ориентирован в поле, что его магнитный момент 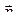 перпендикулярен
перпендикулярен 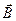 .
.
Следовательно, магнитная индукция внешнего поля может быть определена экспериментально
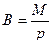 .
.
Но магнитная индукция не зависит, ни от размеров рамки, ни от силы тока, текущего в ней.
|
|
|
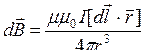
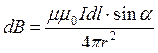 ,
,
μ - относительная магнитная проницаемость среды,
μ0 = 4π∙10-7 Гн/м - магнитная постоянная,
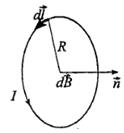
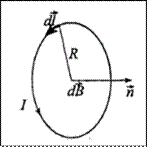
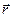 -радиус-вектор, проведенный от элемента тока I ∙ d
-радиус-вектор, проведенный от элемента тока I ∙ d 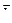 в точку.
в точку.
Применения теоремы позволяют определить индукцию магнитного поля в центре кругового тока, соленоида, отрезка прямого тока.
Индукция магнитного поля:
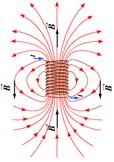
| в центре кругового витка | в центре соленоида | прямолинейного отрезка проводника | бесконечно длинного прямолинейного проводника | ||||||||
|
|
|
| ||||||||
 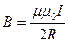
| 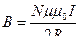
| 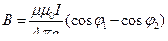
| 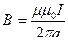
|
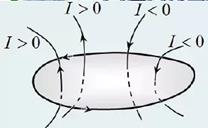
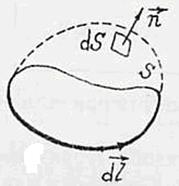
Закон полного тока для магнитного поля в вакууме (теорема о циркуляции): циркуляция вектора магнитной индукции поля в вакууме вдоль замкнутого контура L пропорциональна алгебраической сумме токов, охватываемых этим контуром (т. е. результирующему току через поверхность, натянутую на контур L ).
|
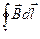 =
= 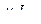 ;
; 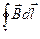 =
= 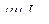
где 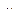 =
= 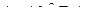 - магнитная постоянная,
- магнитная постоянная,
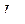 - алгебраическая сумма токов в проводниках, пронизывающих произвольную поверхность S, натянутую на рассматриваемый контур L.
- алгебраическая сумма токов в проводниках, пронизывающих произвольную поверхность S, натянутую на рассматриваемый контур L.
Если учесть, что 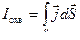 ,
,
|
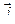 - плотность тока в пределах малого участка площадью dS поверхности S,
- плотность тока в пределах малого участка площадью dS поверхности S, 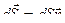 ,
,
 - единичный вектор нормали к площадке dS, из конца которого обход контура L виден происходящим против часовой стрелки (правило правого винта).
- единичный вектор нормали к площадке dS, из конца которого обход контура L виден происходящим против часовой стрелки (правило правого винта).
При подсчете 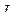 ток, пересекающий поверхность S, считается положительным, если из конца вектора плотности этого тока обход контура L виден происходящим против часовой стрелки.
ток, пересекающий поверхность S, считается положительным, если из конца вектора плотности этого тока обход контура L виден происходящим против часовой стрелки.
Тогда интегральный вид закона полного тока для магнитного поля в вакууме 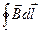 =
= 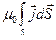 .
.
|
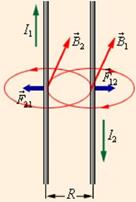
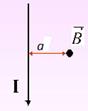
Силовыми линиями магнитного поля являются окружности, центры которых лежат на оси провода с током, а вектор 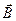 любой из этих окружностей всюду
любой из этих окружностей всюду
имеет один и тот же модуль.
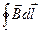 =
= 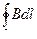 . Вынесем В за знак интеграла. После интегрирования будем иметь:
. Вынесем В за знак интеграла. После интегрирования будем иметь: 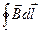
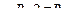
Так как контур L охватывает всего один провод с током, то, согласно закону 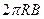 =
= 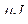 . Следовательно,
. Следовательно, 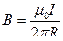 .
.
|
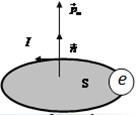
Электрон, движущийся по окружности, подобен круговому контуру с током и, следовательно, характеризуется магнитным моментом:
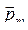 =
=  .
.
Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. В атомах и молекул их электроны, движущиеся по одной орбите, образуют пары. Собственные магнитные моменты электронов в этих парах всегда направлены в противоположные стороны так, что их сумма равна нулю.
Магнитное поле, создаваемое токами, которые не входят в состав рассматриваемой системы, называется внешним по отношению к этой системе.
|
|
|
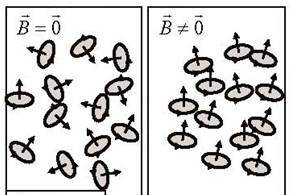
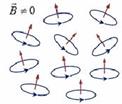
Парамагнитная молекула – это молекула, магнитный момент которой не равен нулю, даже когда внешнего поля нет. Любой атом и молекула с нечетным числом электронов всегда парамагнитны. Такая молекула ведет себя в магнитном поле как рамка с током.
Силы Ампера, с которыми магнитное поле действует на парамагнитную молекулу, стремятся развернуть молекулу так, чтобы ее магнитный момент был направлен по полю, т.е. в ту же сторону, что и вектор магнитный индукции. Этому препятствует тепловое движение молекул.
Под действием внешнего магнитного поля парамагнитные молекулы ориентируются преимущественно по полю, несмотря на то, что тепловое движение стремится разупорядочить их ориентацию. Диамагнитные молекулы во внешнем поле намагничиваются.
Таким образом, какие бы молекулы не входили в состав вещества, если его поместить в магнитное поле, сумма магнитных моментов всех молекул в любом физически бесконечно малом объеме  уже не будет равна нулю. Вещество в таком состоянии называется намагниченным.
уже не будет равна нулю. Вещество в таком состоянии называется намагниченным.
Намагниченность – векторная величина, являющаяся мерой намагничеснности вещества. Показывает магнитный момент единицы объема намагниченного вещества.
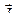 =
= 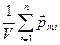 [
[ 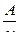 ]
]
Намагниченность вещества называется однородной, если вектор 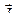 во всех его точках один и тот же. Намагниченность физически бесконечно малого объема вещества всегда можно считать однородной.
во всех его точках один и тот же. Намагниченность физически бесконечно малого объема вещества всегда можно считать однородной.
Напряженность магнитного поля. Связанными (молекулярными) или микротоками называются токи ( 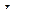 ), обусловленные движением электронов в атомах и молекулах.
), обусловленные движением электронов в атомах и молекулах.
Свободными токами или макротоками ( 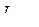 ) называются токи проводимости и конвекционные токи.
) называются токи проводимости и конвекционные токи.
Воспользуемся законом полного тока 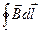 =
= 
|
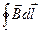 =
= 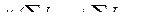 )
)
Будем упрощенно рассматривать каждую молекулу как круговой контур с током  , площадь которого обозначим
, площадь которого обозначим  . Все молекулы будем считать одинаковыми и в среднем одинаково ориентированными. Тогда намагниченность
. Все молекулы будем считать одинаковыми и в среднем одинаково ориентированными. Тогда намагниченность
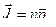
где 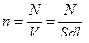 , п - концентрация молекул, S – площадь цилиндра, образованного нанизанных на контур токов,
, п - концентрация молекул, S – площадь цилиндра, образованного нанизанных на контур токов, 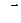 - высота этого цилиндра.
- высота этого цилиндра.
Так как 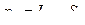 , то
, то 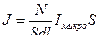
Сумму молекулярных токов, "нанизанных" на весь контур L, можно представить как циркуляцию вектора 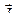 по этому контуру:
по этому контуру:
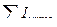 =
= 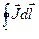 .
.
Тогда закон полного тока для магнитного поля будет иметь вид:
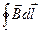 =
= 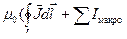 ).
).
Преобразуем выражение 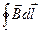 =
= 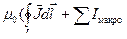 ) к виду
) к виду
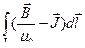 =
= 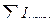 .
.
Напряженность магнитного поля - векторная физическая величина, являющаяся количественной характеристикой магнитного поля. Напряженность магнитного поля не зависит от магнитных свойств среды.
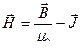
 - напряженность магнитного поля, [А/м];
- напряженность магнитного поля, [А/м];
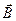 - магнитная индукция, [Тл];
- магнитная индукция, [Тл];
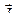 - намагниченность, [А/м];
- намагниченность, [А/м];
μ0 = 4π∙10-7 Гн/м – магнитная постоянная.
В вакууме напряженность магнитного поля совпадает с магнитной индукцией. В среде напряженность магнитного поля определяет тот вклад в магнитную индукцию, который дают внешние источники поля, [А/м].
Закон полного тока для магнитного поля (теорема о циркуляции) в среде:
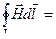
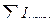 или
или 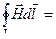
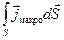 .
.
Намагниченность связана с химическим составом вещества:
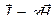 ,
,
 - напряженность магнитного поля, [А/м];
- напряженность магнитного поля, [А/м];
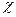 - магнитная восприимчивость -
- магнитная восприимчивость -
физическая величина, характеризующая связь между магнитным моментом (намагниченностью) вещества и магнитным полем в этом веществе.
Магнетик называется однородным, если магнитная восприимчивость во всех его точках одинакова.
Из 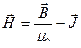 можно выразить
можно выразить 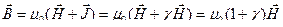 , тогда
, тогда
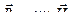 ,
,
где  - магнитная проницаемость - физическая величина, характеризующая связь между магнитной индукцией и напряженностью магнитного поля в веществе.
- магнитная проницаемость - физическая величина, характеризующая связь между магнитной индукцией и напряженностью магнитного поля в веществе.
Величины 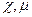 служат характеристиками магнитных свойств вещества, а уравнения
служат характеристиками магнитных свойств вещества, а уравнения 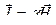 и
и 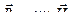 описывают влияние магнитного поля на намагниченность магнетика.
описывают влияние магнитного поля на намагниченность магнетика.
Диамагнетики ( 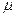 <1) - вещества, способные создавать внутри себя поле, ослабляющее внешнее магнитное поле. У диамагнетиков атомы или молекулы в отсутствие внешнего магнитного поля не имеют магнитных моментов, так как магнитные моменты всех электронов в отсутствии внешнего магнитного поля взаимно скомпенсированы. К диамагнетикам относятся инертные газы, водород, азот и др.
<1) - вещества, способные создавать внутри себя поле, ослабляющее внешнее магнитное поле. У диамагнетиков атомы или молекулы в отсутствие внешнего магнитного поля не имеют магнитных моментов, так как магнитные моменты всех электронов в отсутствии внешнего магнитного поля взаимно скомпенсированы. К диамагнетикам относятся инертные газы, водород, азот и др.
Парамагнетики ( 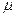 >1) - вещества, намагничивающееся во внешнем магнитном поле по направлению поля.
>1) - вещества, намагничивающееся во внешнем магнитном поле по направлению поля.
В отсутствие внешнего магнитного поля парамагнетики имеют отличный от нуля магнитный момент. Примерами парамагнетиков являются щелочные и щелочно-земельные металлы.
Ферромагнетики ( 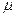 >>1) – вещества, у которых ниже определенной температуры Кюри магнитные моменты электронов выстраиваются параллельно друг другу.
>>1) – вещества, у которых ниже определенной температуры Кюри магнитные моменты электронов выстраиваются параллельно друг другу.
В результате возникают области самопроизвольного намагничивания, называемые доменами. Они имеют размеры порядка 1-10 мкм. Среди химических элементов ферромагнитными свойствами обладают Fe, Со и Ni (3 d-металлы) и редкоземельные металлы. При отсутствии внешнего магнитного поля магнитные моменты отдельных доменов ориентированы хаотически, поэтому результирующий магнитный момент ферромагнетика равен нулю, и он не намагничен. Внешнее поле ориентирует по полю магнитные моменты не отдельных атомов, как это имеет место в случае парамагнетиков, а целых областей, т.е. доменов. Поэтому с ростом напряженности магнитного поля 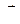 намагниченность
намагниченность 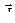 и магнитная индукция
и магнитная индукция 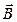 даже в сравнительно слабых полях растет очень быстро. При температуре Кюри все домены в ферромагнетике разрушатся, и он переходит в состояние парамагнетика. Температура Кюри для железа 753 °С, для никеля 365 °С, а для кобальта 1000°С.
даже в сравнительно слабых полях растет очень быстро. При температуре Кюри все домены в ферромагнетике разрушатся, и он переходит в состояние парамагнетика. Температура Кюри для железа 753 °С, для никеля 365 °С, а для кобальта 1000°С.
Дата: 2019-04-23, просмотров: 332.
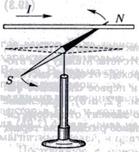
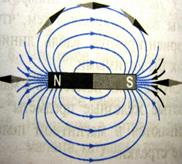
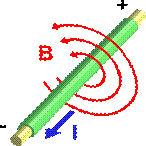
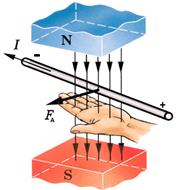
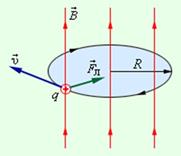 Поясняющий рисунок
Поясняющий рисунок
 Поясняющий рисунок
Поясняющий рисунок