Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

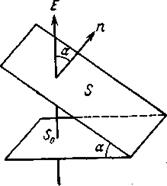
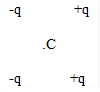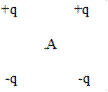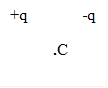применяется наряду с прин­ципом суперпозиции полей для расчета электростатических полей в вакууме. Использование теоремы Остроградского - Гаусса особенно удобно в случае полей, которые обладают заранее известной симметрией, обусловленной симметрией в конфигурации зарядов - источников рассматриваемого поля.

Потоком напряженности электрического поля сквозь малый участок площадью dS поверхности, проведенной в поле, называется физи­ческая величина

,

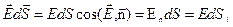где 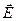 - вектор напряженности электрического поля в точках площадки dS ,

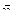 - единичный вектор, нормальный к площадке dS ,

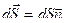 - вектор площад­ки.

Поток напряженности электрического поля сквозь поверхность равен алгебраической сумме потоков сквозь все малые участки этой поверхности:

.

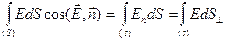Теорема Остроградского-Гаусса: поток напряженности электростати­ческого поля в вакууме сквозь произвольную замкнутую поверхность, проведенную в поле, пропорционален алгебраической сумме электрических зарядов, охватываемых этой поверхностью

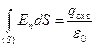, где e ₀ = 8,85×10^-12 Ф/м – электрическая постоянная.

Напряженность электростатического поля внут­ри проводника равна нулю .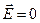

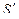Покажем это. Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу  радиусом r'< R. Внутри сфе­ры S' зарядов нет, так как все они расположены на внешней сферической поверхности, т. e.

 

Следовательно, по теореме Гаусса, напряженность электростатического поля внут­ри полой равномерно заряженной сферы будет равна нулю .

 

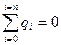
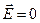Применения теоремы Гаусса

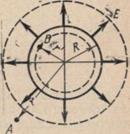
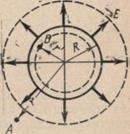
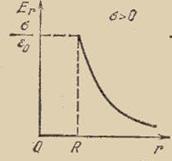
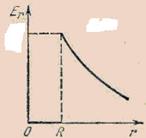
 1.Напряженность электростатического поля, соз­даваемого равномерно заряженной сферической поверхностью: .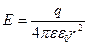

Покажем это. Предположим, что сферическая поверхность радиусом R несет на себе равномерно распределенный заряд q, т. е. поверхностная плотность заряда в любой точке сферы будет одинакова.

Возьмем точку А, отстоящую от центра сферической поверх­ности на расстоянии r. Мысленно проведем через точку A новую сферическую поверхность S, симметричную заряженной сфере.

Поток вектора напряженности через поверхность S: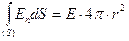

Но по теореме Гаусса: .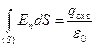

Приравниваем и получаем: .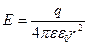

Следовательно, напряжен­ность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.

2. Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром радиуса R): .

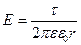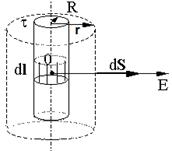
Покажем это. Предположим, что нить заряжена с постоянной поверхностной плотностью . Про­ведем коаксиальную цилиндрическую поверхность.

Поток вектора напряженности через поверхность S:

.

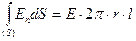Но по теореме Гаусса

; , , .

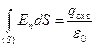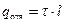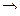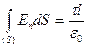Приравниваем и получаем: .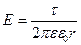

 

Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью обратно пропорциональна расстоянию от нее.

3.Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью: .

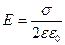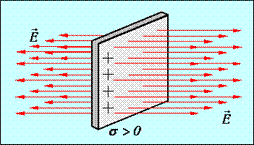
Покажем это. Предположим, что плоскость имеет бесконечную протяжен­ность и заряд на единицу площади равен .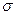

Из законов симмет­рии следует, что поле направлено всюду перпендикулярно плос­кости и, если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковыми по ве­личине.

Ограничим часть заряженной плоскости  воображаемым прямоугольным ящиком  (Гауссова поверхность) таким обра­зом, чтобы ящик рассекался пополам.

Поток вектора напряженности через поверхность S:

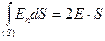
Но по теореме Гаусса

; , ,

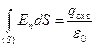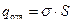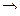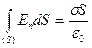
Приравниваем и получаем: .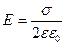

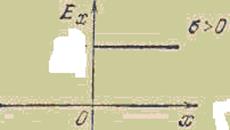
Следовательно, напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, не зависит от расстояния от нее.

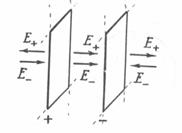
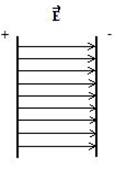
4.Напряженность поля, создаваемого двумя бес­конечными параллельными плоскостями, заряженными разно­именно с одинаковыми плотностями: .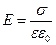

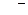Покажем это. Напряженность поля между двумя бес­конечными параллельными плоскостями, имеющими поверхностные плотности зарядов ( ) и (+ 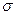), равна сумме напряженностей полей, создаваемых обеими пластинами, т. е.

+ = .

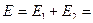
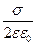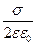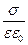Вне пластин векторы напряженности от каждой из них направлены в про­тивоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю (Е = 0).

3.1.Как зависит сила взаимодействия двух точечных зарядов от значения зарядов?

3.2.Как зависит сила взаимодействия двух точечных зарядов от расстояния между ними?

3.3.Изменится ли сила взаимодействия между двумя точечными заряженными телами, если расстояние между зарядами уменьшить в 3 раза?

3.4.Как изменится сила взаимодействия между двумя точечными заряженными телами, если каждый заряд уменьшить в 3 раза?

3.5.В вершинах квадрата находятся равные по модулю заряды. Как направлена сила, действующая на отрицательный точечный заряд, помещенный в точку С, в центре квадрата?  

       

3.6.В вершинах квадрата находятся равные по модулю заряды. Как направлена сила, действующая на положительный точечный заряд, помещенный в точку А, в центре квадрата?   

3.7.Какая физическая величина называется напряженностью электрического поля?

3.8.Напряженность электрического поля измеряют с помощью пробного заряда q. Как изменится модуль напряженности, если пробный заряд увеличить в 4 раза?

3.9.Как изменится напряженность электрического поля, созданного точечным зарядом, при уменьшении расстояния от него в 3 раза?

3.10.На точечный заряд, равный 10 мкКл, находящийся в воздухе, в некоторой точке электрического поля действует сила 10 мкН. Вычислите напряженность поля в данной точке.

3.11.Определите направление напряженности электрического поля положительного заряда q в точке А.                                                       

3.12.Определите направление напряженности электрического поля положительного заряда q в точке А.

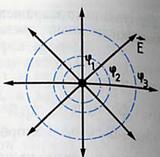
3.13.Определите направление напряженности электрического поля двух зарядов в точке С, при условии равенства значений зарядов и расстояний от зарядов до точки.  

3.14.Определите направление напряженности электрического поля двух зарядов в точке С, при

условии равенства модулей зарядов и расстояний от зарядов до точки.

3.15.Определите направление напряженности электрического поля двух зарядов в точке С, при условии равенства модулей зарядов и расстояний от зарядов до точки.

3.16.Найдите силу притяжения между ядром атома во­дорода и электроном. Диаметр атома водорода 10^{-10 м}, заряд ядра равен по величине и противоположен по знаку заряду электрона.[9,23∙10^-8 Н]

3.17.Во сколько раз сила гравитационного притяжения между двумя протонами меньше силы их кулоновского отталкивания? [1,25∙10³⁶]

3.18.В вершинах равностороннего треугольника находятся одинаковые положительные заряды 2 нКл. Какой отрицательный заряд необходимо поместить в центр треугольника, чтобы сила притяжения с его стороны уравновесила силы отталкивания положительных зарядов?

3.19.В центр квадрата, в вершинах которого нахо­дится по заряду в 7 нКл, помещен отрицательный за­ряд. Найдите величину этого заряда, если результи­рующая сила, действующая на каждый заряд, равна нулю.[11,5 нКл]

3.20. Шарик плотностью 11,3 г/см³ помещен в жидкость, плотность которой    1,26 г/см³. Определите заряд шарика, если в однородном электростатическом поле напряженностью 4 кВ/ c м шарик оказался взвешенным в жидкости. [16,1нКл]

3.21.Найдите напряженность электрического поля в точ­ке, лежащей посередине между точечными зарядами 8 нКл и -6 нКл. Расстояние между заря­дами равно 10 см.[5,04∙10⁴ В/м]

3.22. В вершинах квадрата со стороной 5 см находятся одинаковые положительные заряды по 2 нКл. Определите напряженность электрического поля: 1) в центре квадрата, 2) в середине одной из сторон квадрата.

Потенциал

 - энергетическая характеристика поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля.

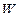Потенциалом электрического поля называется физическая величина, равная отношению потенциальной энергии , которую приобретает точечный пробный заряд, помещенный в рассматриваемую точку поля, к величине  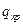этого заряда

,  

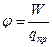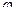 - потенциал, [В] (Вольт[18]);

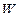 - потенциальная энергия, [Дж];

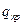- пробный заряд, [Кл].

Потенциал бесконечно уда­ленной точки принимается равным нулю.

Эквипотенциальная поверхность - совокупность точек, имеющих равный потенциал.

Эквипотенциальные поверхности пер­пендикулярны к силовым линиям и с их помощью также можно изобразить графически электростатическое поле.

 

 

Принцип суперпозиции: когда поле образовано несколькими произвольно располо­женными зарядами, потенциал его в данной точке равен алгебраической сумме потенциалов, создавае­мых каждым зарядом в отдельности, т. е.

.

Рис.

Работа по перемещению заряда:  ;

l

Покажем это. Сначала рассмотрим первую формулу .

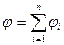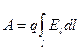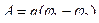
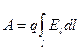Работа, совершаемая кулоновскими силами при малом перемещении 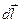 точечного заряда q из одной точки электростатического поля в другую, по определению, равна

= .

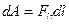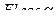dA >0, если работа совершается си­лами поля;

dA<0, если работа совершается внешними силами.

Элементарная работа на участке 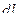равна

Интегрируя последнее выражение, получим, что работа сил поля при перемещении q вдоль линии будет равна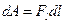

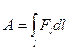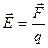; но , но .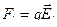

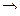
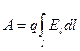Работа по перемещению за­ряда из одной точки в другую не зависит от формы пути, по которому движется пробный заряд, а зависит только от положения точек. Следовательно, кулоновская сила является консервативной.

Рассмотрим вторую формулу: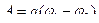  

Работа равна убыли потенциальной энергии W этого заряда, который перемещается в электростатическом поле, т. е.

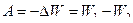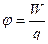, но , следовательно, 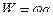, тогда .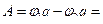

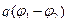Напряжение:

Определение 1. Напряжение - разность значений потенциала в начальной и конечной точках траектории .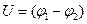

Определение 2. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля .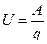

Обозначается U .

Единица [В] (Вольт).

Разность потенциалов (напряжение) является важной харак­теристикой электростатического поля, так как при любых расче­тах важно знать не абсолютные значения потенциалов в каких-либо двух точках поля, а именно разность потенциалов между ними.

Когда говорят о потенциале в данной точке поля, подразуме­вают разность потенциалов между этой точкой и другой, потен­циал которой условно считают равным нулю (например, прини­мают равным нулю потенциал Земли).

Связь между потенциалом и напряженностью электростатического поля          Так как работа может быть выражена через силовую 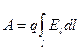и энергетическую характеристики поля 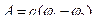, то 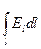= 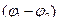, следовательно, 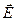=  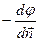или

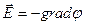[19].

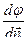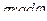= - характеризует быстроту изменения потенциала в направлении силовой линии

Вектор напряженности численно равен градиенту потенциала, но направлен в противоположную сторону - в сторону падения потенциала.

 

Сделанные выше выводы имеют следующие следствия:

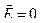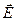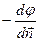1. Потенциал внутри проводника не изменяется, так как напряженность поля внутри проводника , но = , следовательно, .

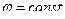2.Расчет потенциалов:

Точечного заряда

	Металлической сферы		Дата: 2019-04-23, просмотров: 253. ⇐ Предыдущая891011121314151617Следующая ⇒ Материалы представленные на сайте исключительно с целью ознакомления пользователям Интернета и не преследуют коммерческих целей или нарушение авторских прав. © 2018 - 2024