Уравнение затухающих гармонических колебаний в дифференциальной форме имеет вид:
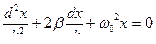 ,
,
где β=const > 0 — коэффициент затухания,
ω0 - циклическая частота свободных незатухающих колебаний той же системы.
Решением этого уравнения является:  ,
,
|
 ,
, 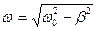 .
.
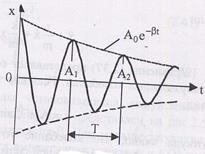
Следовательно, затухающие колебания не являются периодическими. Максимальное значение колеблющейся величины никогда не повторяется.
Однако при затухающих колебаниях величина x обращается в нуль, а также достигает максимальных и минимальных значений через равные промежутки времени. Поэтому величины T и ω условно называют периодом (условным периодом) и циклической частотой (условной циклической частотой) затухающих колебаний.
Величина  называется амплитудой затухающих колебаний, соответственно А0 - начальной амплитудой.
называется амплитудой затухающих колебаний, соответственно А0 - начальной амплитудой.
Логарифмическим декрементом затухания называется безразмерная величина  , равная натуральному логарифму отношения значений амплитуды затухающих колебаний в моменты времени t и t + T .
, равная натуральному логарифму отношения значений амплитуды затухающих колебаний в моменты времени t и t + T .
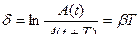 =
=  .
.
Вынужденные колебания
совершаются под действием внешней периодически изменяющейся силы, которую называют вынуждающей.
Вынуждающей, или возмущающей силой называется переменная внешняя сила, приложенная к системе и вызывающая ее вынужденные механические колебания.
Дифференциальное уравнение вынужденных колебаний имеет вид:
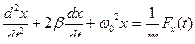 .
.
Если возмущающая сила изменяется по гармоническому закону, т.е. FX = F 0 cos 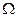 t , то установившиеся вынужденные колебания маятника также гармонические с той же частотой:
t , то установившиеся вынужденные колебания маятника также гармонические с той же частотой:
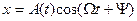 .
.
Амплитуда этих колебаний А и сдвиг фаз 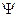 между смещением и возмущающей силой зависят от соотношения между циклическими частотами вынужденных колебаний
между смещением и возмущающей силой зависят от соотношения между циклическими частотами вынужденных колебаний 
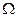 и свободных незатухающих колебаний маятника
и свободных незатухающих колебаний маятника  :
:
|
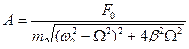 ,
, 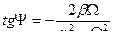 .
.
Механическим резонансом называется резкое возрастание амплитуды вынужденных механических колебаний при приближении циклической частоты возмущающей силы к значению 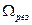 .
.
 ,
,  .
.
По мере увеличения коэффициента затухания пики на резонансных кривых быстро сглаживаются, а резонансная частота медленно уменьшается.
4.1.Какая величина называется:
а) периодом,
б) частотой,
в) амплитудой,
г) фазой колебания,
д) коэффициентом затухания,
е) логарифмическим декрементом затухания?
4.2.Какой вид имеют дифференциальные уравнения: а) свободных незатухающих колебаний, б) затухающих колебаний, в) вынужденных колебаний?
|
4.4.Что такое резонанс и когда он возникает?
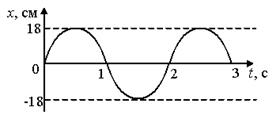
4.5.Пользуясь графиком, найдите чему равен модуль скорости в момент времени  с.
с.
4.6.Напишите уравнение гармонического колебательного движения с амплитудой в 5 см , если за 1 мин совершается 150 колебаний и начальная фаза колебаний равна 45°.Найдите закон изменения скорости и ускорения. Чему равна максимальная возвращающая сила, если масса тела 100 г? Найдите полную механическую энергию системы. Начертите график этого движения. [х=0,05cos(5πt+π/4); 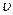 =-0,25πsin(5πt+π/4); а=-1,25π2cos(5πt+π/4); F=0,125 π2 Н]
=-0,25πsin(5πt+π/4); а=-1,25π2cos(5πt+π/4); F=0,125 π2 Н]
4.7.Через сколько времени от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний равен 24 с, начальная фаза равна нулю.[2 с]
4.8.Груз, подвешенный к спиральной пружине, колеблется по вертикали с амплитудой 8 см. Определите жесткость пружины, если известно, что максимальная кинетическая энергия груза составляет 0,8 Дж. [250 Н/м]
4.9.Два колеблющихся с одинаковыми амплитудами математических маятника имеют одинаковые массы, а длины отличаются в 1,5 раза. Определите, какой из маятников обладает большей энергией и во сколько раз. [Маятник большей длины, в 1,5 раза].
4.10.Однородный диск радиусом 20 см колеблется около горизонтальной оси, проходящей на расстоянии 15 см от центра. Определите период колебаний диска относительно этой оси.[1,07 c]
4.11.Однородный стержень длиной 60 см может свободно вращаться вокруг горизонтальной оси, проходящей через верхний конец стержня. Стержень отклонили на угол 0,01 рад и отпустили. Считая колебания малыми, опреде  лите период колебаний стержня. [1,27 с]
лите период колебаний стержня. [1,27 с]
4.12.Определите коэффициент затухания математического маятника, если за промежуток времени 4,8∙10-2 с маятник теряет 99 % своей полной механической энергии. [4,8∙10-3 с]
4.13.Частица совершает прямолинейные затухающие колебания с периодом 4,5 с. Начальная амплитуда колебаний 0,16 м, а амплитуда после 20 полных колебаний 0,01 м. Определите коэффициент затухания и логарифмический декремент затухания. [3,1∙10-2 с; 0,14]
4.14.Логарифмический декремент затухания маятника равен 0,003. Определите число полных колебаний, которые должен сделать маятник, чтобы амплитуда уменьшилась в два раза. [231]
4.15.Колебательный контур содержит соленоид (длина 5 см, площадь поперечного сечения 1,5 см2, число витков 500) и плоский конденсатор (расстояние между пластинами 1,5 мм, площадь пластин 100 см2). Определите частоту собственных колебаний контура.[8,4∙107 рад/ c]
4.16.Вычислите частоту собственных колебаний в контуре с активным сопротивлением, равным нулю, если индуктивность этого контура равна 12 мГн, а его емкость составляет 0,88 мкФ. Как изменится частота колебаний, если в контур включить последовательно еще три таких же конденсатора? [9,7 кГц; увеличится в 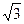 раз]
раз]
4.17.Катушка индуктивностью 1 мГн и воздушный конденсатор, состоящий из двух круглых пластин диаметром 20 см каждая, соединены параллельно. Расстояние между пластинами 1 см. Определите период колебаний. [104 мкс]
4.18.Найдите промежуток времени, за который амплитуда колебаний силы тока в контуре с добротностью, равной 5000, уменьшается в 2 раза, если частота свободных колебаний в контуре 2,2 МГц.
4.19.Колебательный контур состоит из конденсатора емкостью 0,2 мкФ и катушки индуктивностью 5,07 мГн. При каком логарифмическом декременте затухания разность потенциалов на обкладках конденсатора за 10-3 с уменьшится в три раза? Чему при этом равно сопротивление контура?
Волны
– распространяющиеся в пространстве колебания.

Механические (упругие волны) волны - механические возмущения (деформации), распространяющиеся в упругой среде.
Бегущими волнами называются волны, которые, в отличие от стоячих волн, переносят энергию в пространстве.
Например, для волн в твердой среде такой величиной может служить вектор смещения частицы среды из положения равновесия или три его проекции на оси координат. Для характеристики продольных волн в газе или жидкости обычно пользуются избыточным давлением колеблющейся среды, равным разности между ее переменным и равновесным давлениями.
Волновой поверхностью, или фронтом волны, называется геометрическое место точек, в которых фаза колебаний имеет одно и то же значение.
Для всех точек одной волновой поверхности разность t - t 0
одинакова.
 Через каждую точку среды, охваченной волновым движением, можно провести одну волновую поверхность, соответствующую значению фазы колебаний в этой точке в рассматриваемый момент времени.
Через каждую точку среды, охваченной волновым движением, можно провести одну волновую поверхность, соответствующую значению фазы колебаний в этой точке в рассматриваемый момент времени.
Выделяют плоские волны и сферической волны.
|
Волна называется сферической, если ее волновые поверхности имеют вид концентрических сфер. Центр этих сфер называется центром волны. Такого рода волны возбуждаются в однородной изотропной среде уединенным точечным источником.
Уравнения волны
Длина волны – минимальное расстояние между двумя точками, находящимися в одной и той же фазе колебаний.
Обозначается 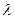 . Единица [
. Единица [ 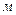 ].
].
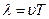 ;
;  ,
,
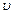 - скорость волны, [м/c];
- скорость волны, [м/c];
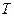 - период, [с];
- период, [с];
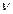 - частота, [Гц].
- частота, [Гц].
С другой стороны, длина волны равна расстоянию между двумя ближайшими точками среды, в которых разность фаз колебаний равна 2π.
 ,
,
k - волновое число
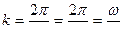 .
.
Волновое уравнение (дифференциальное уравнение волны):
 +
+ 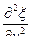 +
+  =
= 
или 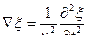 , где
, где  - оператор Лапласа (лапласиан[28])
- оператор Лапласа (лапласиан[28])
Решением этого уравнения для плоской волны, распространяющейся вдоль положительного направления оси ОХ является уравнение плоской волны, , являющееся :
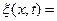
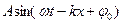 ,
,
А=const - амплитуда колебаний (амплитуда волны),
ω= 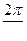 - циклическая (круговая) частота волны,
- циклическая (круговая) частота волны,
Ф =  - фаза плоской волны.
- фаза плоской волны.
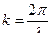 - волновое число.
- волновое число.
 -начальная фаза колебаний.
-начальная фаза колебаний.
Уравнение синусоидальной расходящейся сферической волны имеет вид:
 .
.
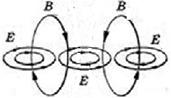
Электромагнитное поле – особая форма материи, существующая вокруг движущихся с ускорением заряженных тел или частиц.
|
|
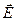 и магнитной индукции
и магнитной индукции  перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны.
перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны.
2.Электромагнитные волны распространяются в веществе с конечной скоростью ( 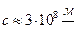 - скорость электромагнитных волн в вакууме).
- скорость электромагнитных волн в вакууме).
Для вакуума 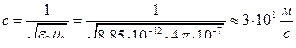 .
.
В других средах: 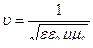
3.При распространении электромагнитных волн в пространстве создаются токи смещения, которые определяются изменяющимся со временем электрическим полем.
Ток смещения - величина, пропорциональная скорости изменения электрического поля во времени.
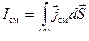 =
= 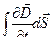 =
= 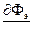 .
.
Уравнения Максвелла
| в интегральной форме | в дифференциальной форме |
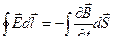
| 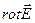 *=- *=- 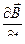
|
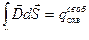
| 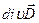 **= **= 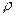
|
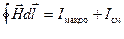
| 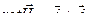 ; ; 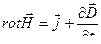
|
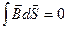
| 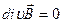
|
|
| |
Материальные уравнения характеризуют электрические и магнитные свойства среды.
  
|
1- е уравнение, представляет закон Фарадея.
| в интегральной форме | в дифференциальной форме |
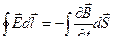
| 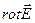 *=- *=- 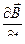
|
где 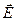 - вектор напряженности электрического поля,
- вектор напряженности электрического поля,
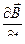 - изменение вектора магнитной индукции.
- изменение вектора магнитной индукции.
Переменное магнитное поле создает в любой точке пространства вихревое индуцированное электрическое поле независимо от того, находится в этой точке проводник или нет.
2-е уравнение, демонстрирующее закон полного тока для магнитного поля (теорема о циркуляции).
| в интегральной форме | в дифференциальной форме |
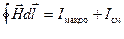
| 
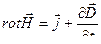
|
где 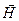 - напряженность магнитного поля,
- напряженность магнитного поля,
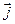 - вектор плотности тока.
- вектор плотности тока.
Уравнение показывает, что циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру  равна алгебраической сумме макротоков и тока смещения сквозь поверхность, натянутую на этот контур.
равна алгебраической сумме макротоков и тока смещения сквозь поверхность, натянутую на этот контур.
3-е уравнение, выражающее теорему Гаусса, которая доказывается в электростатике и переносится без изменения в теорию переменных электрических и магнитных полей (электродинамику).
| в интегральной форме | в дифференциальной форме |
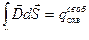
| 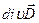 **= **= 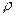
|
где  - вектор электрической индукции (электрического смещения),
- вектор электрической индукции (электрического смещения),
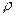 - объемная плотность свободных зарядов.
- объемная плотность свободных зарядов.
Поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду.
4- уравнение магнитостатики, выражающее теорему Гаусса.
| в интегральной форме | в дифференциальной форме |
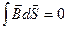
| 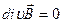
|
Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Это эквивалентно тому, что в природе не существует «магнитных зарядов», которые создавали бы магнитное поле, как электрические заряды создают электрическое поле. Теорема Гаусса для магнитной индукции показывает, что магнитное поле является вихревым.
Объемная плотность энергии электромагнитного поля:  .
.
Из закона сохранения энергии и соотношения между модулями векторов 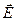 и
и 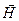 электромагнитного поля следует
электромагнитного поля следует
 или
или  .
.
Производная от плотности энергии по времени равна.
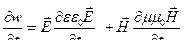 или
или 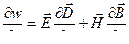 .
.
Дата: 2019-04-23, просмотров: 683.