Для выходного вала редуктора рассчитаны следующие величины: Т4=601,7 Н·м, n5=57,3 об/мин, ширина колеса: b3=64 мм, предел прочности sв=850 МПа, диаметр вала в месте посадки колеса считаем 55 мм. Диаметр колеса – 256 мм.
Выбираем материал вала сталь 45, улучшенная. [t]=19 МПа, предел текучести sт = 450 МПа, предел прочности sв=750 МПа. Запишем геометрические параметры вала (см. рис. 7): a=60 мм, b=60 мм, c=55 мм, l=a+b=120 мм. Вал нагружен силами Ft=2T/d=2·601,7/0,2425=4962,5 Н, Fa=Ft·tgβ=Ft·tg0˚=0 Н, Fr=Ft·tgα=Ft·tg20˚=1806,2 Н, действующими в полюсе зацепления, и крутящим моментом Т4 на выходном конце муфты.
Определяем допускаемую радиальную нагрузку на выходном конце вала, полагая, что редуктор общего назначения(с. 298[3]):
(2.7.1)
Для Т4=601,7 получим FM=250·24,5=6125 Н.
Определяем реакции в опорах и строим эпюры изгибающих и крутящих моментов (см. рис. 7).
рис. 7 Эпюры нагрузок выходного вала
Рассмотрим реакции от силы Fr, действующей в вертикальной плоскости. Сумма проекций Fr=A1+B1. Сумма моментов относительно опоры А: -Fr·a+B1·l=0. Из последнего равенства получим B1=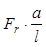 
=1926,5∙0,5=963,25 Н. Тогда A1=Fr-B1=1926,3-963,25=963,25 Н.
Реакция от сил Ft и FM, действующих в горизонтальной плоскости (FM прикладываем так, чтобы она увеличивала прогиб от Ft – худший случай). Проекции сил A2+B2+FM-Ft=0; сумма моментов: -Ft·a+B2·l+FM·(l+c)=0. Тогда рассчитаем: B2=Ft·a/l - FM·(l+c)/l=4962,5·0,5 – 6125·175/120= -6451 Н. Знак «-» значит, что реальная реакция направлена противоположно тому направлению, которое мы выбрали. A2=Ft-FM-B2= 5288,5 Н.
Для построения эпюр крутящих и изгибающих моментов воспользуемся формулами со страницы 298[3].
Момент от радиальной силы
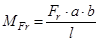(2.7.2)
Момент от окружной силы
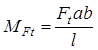(2.7.3)
Момент от силы на выходном конце вала
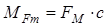(2.7.4)
Рассчитаем эти значения:
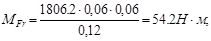
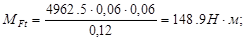
Расчёт на прочность. Просчитываем два предполагаемых опасных сечения (см. рис. ): сечение I-I под колесом, ослабленное шпоночным пазом, и сечение II-II рядом с подшипником, ослабленное галтелью по формуле
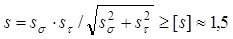(2.7.5)
где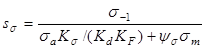 
- запас сопротивления усталости только по изгибу; (2.7.6)
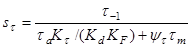- запас сопротивления усталости только по кручению;
В этих формулах σа и τa – амплитуды переменных составляющих циклов напряжений, а σm и τm – постоянные составляющие. ψσ и ψτ – коэффициенты, корректирующие влияние постоянной составляющей цикла напряжений на сопротивление усталости. σ-1 и τ-1 – пределы выносливости. Kd, KF – масштабный фактор шероховатости поверхности; Kσ и Kτ – эффективные коэффициенты концетрации напряжений при изгибе и кручении.
Для первого сечения изгибающий момент
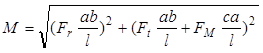(2.7.7)
Подставим числовые значения и получим
.
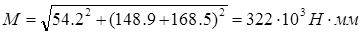Крутящий момент Т=601,7·103 Н·мм.
Напряжение изгиба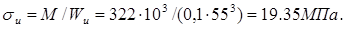 
Напряжение кручения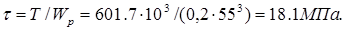 
Определим пределы выносливости по приближённым формулам:
σ-1=0,4 σв=0,4·850=340 МПа; (2.7.8)
τ-1=0,2 σв=0,2·850=170 МПа.
По таблице 15.1[3] Kσ≈1,7 и Kτ≈1,4. По графику (см. рис. 15.5, кривая 2[3]), Kd=0,68. По графику (см. рис. 15.6[3]) для шлифованного вала KF=1. Из рекомендаций (стр. 300[3]) ψσ=0,1 и ψτ=0,05.
При расчёте валов σm=0; σa=M/(0,1d3)=σи=19,35 МПа; τm=τa=0,5τ=9,05 МПа.
Тогда по формулам (2.7.6) получим
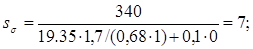
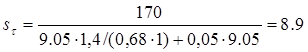
Тогда по соотношению (2.7.5) получим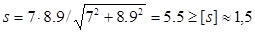 
.
Для второго сечения изгибающий момент 
; крутящий момент Т=601,7 Н·мм.
Напряжение изгиба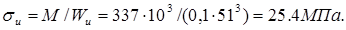 
Напряжение кручения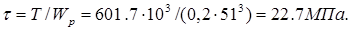 
Принимаем радиус галтели r=2 мм; r/d≈0,03 и находим по таблице 15.1[3] Kσ≈2,3 и Kτ≈1,7. Тогда по формулам (2.7.6) получим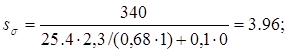 
.
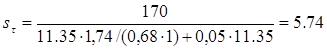Таким образом, по (2.7.5)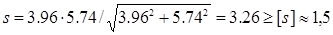 
.
Больше напряжено второе сечение.
Проверяем статическую прочность при перегрузках для второго опасного сечения по формуле:
(2.7.9)
Где σи=M/(0,1d3), (2.7.10)
τ=T/(0,2d3)
Здесь М и Т – изгибающий и крутящий моменты в опасном сечении при перегрузке.
Предельное допускаемое напряжение [σ] принимают близким к пределу текучести σТ: [σ]≈0,8σT (2.7.11)
При перегрузках напряжения удваиваются, тогда для второго сечения
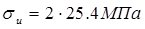и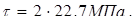 
По (2.7.11) [σ]≈0,8·450=360 МПа. В таком случае по (2.7.9) 
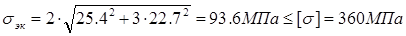. Условие статической прочности выполняется.
Расчёт на жёсткость. По условиям работы зубчатого зацепления опасным является прогиб вала под колесом. Для определения прогиба воспользуемся таблицей 15.2[3]. Средний диаметр на участке l (см. рис. 2.7.1) принимаем равным dш=55 мм. Здесь момент инерции сечения
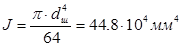(2.7.12)
Прогиб в вертикальной плоскости от силы Fr
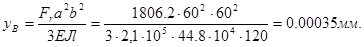(2.7.13)
Прогиб в горизонтальной плоскости от сил Ft и FM:
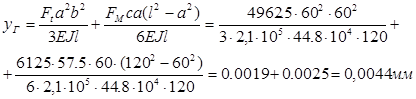(2.7.14)
Суммарный прогиб
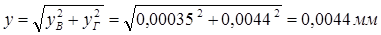(2.7.15)
Допускаемый прогиб по рекомендации на стр. 302[3] [y]≈0,01m=0,01·2,5=0,025мм>0,0044 мм. Необходимое условие работы вала – y<[y] – выполняется.
Расчёт на критические колебания. Пределы, в которых не должна находится частота вращения выходного вала:
0,7nкр≤nвала≤1,3nкр (2.7.16)
Значение критической частоты тихоходного вала определяется по формуле:
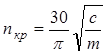(2.7.17)
Массу вала определяем по формуле:
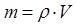(2.7.18)
где ρ – плотность стали (равна 7,8 г/см3), V – объём вала.
Объём вала
(2.7.19)
где dш – диаметр вала под подшипник; l – длина вала.
Вычислим по последней формуле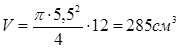 
. Тогда по (2.7.18) m=2220 г=2,22 кг.
c – динамический прогиб вала определяется из завичимости:
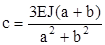(2.7.20)
Учитывая ранее полученные Е=2,1·1011Па и J=87,6·10-8 мм4, получим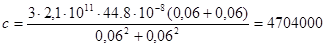 
, откуда по формуле (2.7.17) рассчитаем nкр=13907,5 об/мин. Таким образом, выполняется условие (2.7.16) и вал работает в докритических частотах.
Дата: 2019-05-28, просмотров: 206.
