Основні положення

При аналізі точності геометричних параметрів деталей розрізняють такі поверхні:

1. Номінальні (ідеальні);

2. Реальні (дійсні).

Аналогічно варто розрізняти номінальний і реальний профіль, номінальне і реальне розташування поверхні (профілю). Номінальне визначається номінальними лінійними і умовними розмірами, а реальне – дійсними.

Внаслідок відхилень дійсної форми від номінальної один розмір у різних перетинах деталі може бути різним.

Розміри в поперечному перерізі можна визначити змінним радіусом R, відлічуваним від геометричного центра номінального перетину. Цей радіус називають поточним розміром, тобто розміром, що залежить від положення осьової координати X (Б-Б) і кутової координати φ точки, що лежить на вимірюваній поверхні (φ - кутова координата радіуса R₁).

φ - полярний кут. Контур поперечного перерізу задовольняє умові замкнутості, тобто f (φ) = f (φ+ 2π) (виходить, функція має період 2Т).

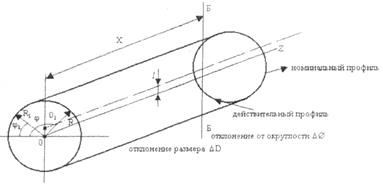
Для аналізу відхилень профілю контур перетину дійсної поверхні можна характеризувати сукупністю гармонійних складових із різними частотами.

Для аналітичного зображення дійсного профілю (контуру перетину) поверхні використають розкладання функції погрішностей f(φ) у ряд Фур'є.

Відхилення ΔR січного розміру R (при обраному значенні Х) від номінального (постійного) розміру R₀, можна виразити залежністю:

ΔR=R-R₀=f(φ)

Розглядаючи відхилення ΔR радіуса-вектора в полярній системі координат як функцію полярного кута φ, можна представити відхилення контуру поперечного переріза деталі у вигляді ряду Фур'є:

,

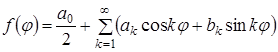де 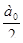- нульовий член розкладання

а_к, b_к - коефіцієнти ряду Фур'є коливань гармоніки.

К - порядковий номер. Ряд Фур'є можна представити також у вигляді:

,

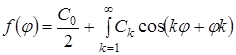де С_к - амплітуда коливань гармоніки.

φ_k - початкова фаза.

Функція f(φ) визначається сукупністю величин С_к, (спектра амплітуд) і φ_k (спектра фаз).

Далі використаємо ряд з обмеженим числом членів, тобто тригонометричний поліном:

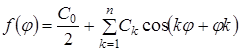
Відповідно до теорії Фур'є, нульовий член розкладання в загальному випадку є середнім значенням f(φ) за період 2π :

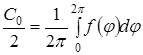, тобто  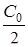-є постійна, складова відхилення поточного розміру.

1-й член розкладання С₁cos(φ + φ₁₎, виражає розбіжність центра обертання О с геометричним центром перетину О (ексцентриситет), тобто відхилення розташування поверхні. Тут С₁, φ₁ - амплітуда й фаза. Члени ряду, починаючи із 2-го і до К = р утворять спектр відхилень форми деталі в поперечному перерізі.

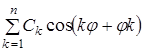
При цьому 2-й член ряду 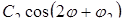 - виражає овальність, 3-й  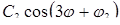- огранювання із 3-х верховим профілем. Наступні члени ряду, що мають номер К > р, виражають хвилястість, при досить великій кількості членів ряду одержуємо високочастотні складові, що виражають шорсткість поверхні.

Аналогічно можна представити відхилення контуру циліндричної поверхні в поздовжньому перерізі, але умова замкнутості контуру в цьому випадку не виконується, де z- змінна, що відлічується уздовж осі циліндра.

Уявивши циліндричну систему координат R, φ , Z і умовно прийнявши, що період Т=2Т, представимо відхилення контуру в поздовжньому перерізі f(z) у вигляді тригонометричного полінома:

,

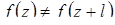де 0≤z≤ℓ

при К= 1

; ,

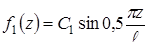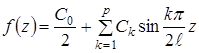де К- порядковий номер члена.

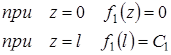
Перший член розкладання характеризує нахил утворюючого циліндра (конусоподібність).

Другий характеризує опуклість контуру в поздовжньому перерізі. Цей же 2-й - при наявності зсуву фази виражає сідлоподібність тощо.