ОСНОВНІ ВІДХИЛЕННЯ - граничні відхилення (верхнє або нижнє), що визначають положення поля допуску щодо нульової лінії.
Для всіх полів допусків, розташованих нижче 0 лінії, основним (найближчим) є верхнє відхилення (es або ЕS). а для полів допусків, розташованих вище 0 лінії - ei або EI – нижнє відхилення.
Усього для валів й отворів передбачено по 28 рядів основних відхилень, які позначаються однією або двома буквами латинського алфавіту – прописні для отворів і рядкові - для валів.
Таблиця 1
| Поля допусків отворів | A | B | C | D | CD | E | EF | F | G | FG | H | I | IS | K | |
| Поля допусків вала | a | b | c | d | cd | e | ef | f | g | fg | h | i | is | k | |
| Поля допусків отворів | M | N | P | R | S | T | U | Y | X | V | Z | ZA | ZB | ZC
| |
| Поля допусків вала | m | n | p | r | s | t | u | y | x | v | z | za | zb | zc
| |
Основний отвір позначається літерою Н (Е1 - О).
Основний вал - h (es = 0).
Ряди основних відхилень від А (а) до Н (h) призначені для утворення посадок із зазором, від I (i) до N (n) - перехідних, і від P (p) до ZC (zс) - з гарантованим натягом.
Для кожного літерного позначення величина і знак основного відхилення, а також допуск наведені в ДЕРЖСТАНДАРТі 25346-89.
Друге (не основне) відхилення визначається із залежностей:
EI(ei) = ES(es) - Т або ES(es) = EI(ei) + Т (рис. 1)
 |
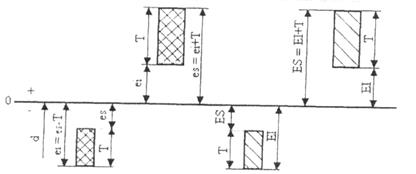Рис. 1 Основні відхилення
Для валів j й js й отворів J й JS поле допуску розташовується симетрично нульової лінії. Основні відхилення, що позначаються однією і тією ж літерою, однакові за величиною, але протилежні за знаком EI=-es для А-Н, ES = -ei для I-ZC.
Із цього правила зроблене виключення для розмірів понад 3 мм для отворів J, К, М та N з допусками по 3-8 квалітетам і для отворів від Р до ZC з допусками по 3-7 квалітетам, для яких застосовується правило:
ES=~-ei+Δ, де 
- різниця між допуском розглянутого квалітету і допуском найближчого більш точного квалітету.
ПОЛЕ ДОПУСКУ В ЕСКД утворюється з’єднанням основного відхилення і квалітету:
для валів: h6, d10, s7, js5; для отворів: Н6, D10, S7, JS5. За основним відхиленням і допуском визначається і друге граничне відхилення, що обмежує дане поле допуску: EI(ei) = ES(es) - Т ES(es) = EI(ei)+T .
Для тих полів допусків, у яких основним відхиленням є верхнє, нижнє визначається:
для вала: es = ei – Td;
для отвору: ES = EI – TD.
Якщо нижнє відхилення є основним, тоді:
для вала: es = ei + Td;
для отвору: ES = EI + TD.
Одиниця допуску і квалітет
У системі ІSО принципово допускаються будь-які з’єднання основних відхилень і квалітетів. Теоретично для кожного з розмірів до 500 мм з’єднанням до 20 квалітетів і 28 основних відхилень можна утворити більш 520 полів допусків валів і 518 полів допусків отворів. Величина основного відхилення для більшості полів допусків не залежить від КВАЛІТЕТУ (ступеня точності) - це сукупність допусків, що відповідають однаковому ступеню точності для всіх номінальних розмірів.
Квалітет позначається порядковим номером, що зростає зі збільшенням допуску. Всього передбачено20 квалітетів (01, 0, 1, 2, 3, ..., 18).
У цих квалітетів стандартом передбачені посадки. Скорочено допуск по одному із квалітетів позначається латинськими літерами, наприклад Н7.
Допуск посадки IT = ai, де а - коефіцієнт, що залежить від квалітету, i - одиниця допуску.
Практикою встановлено, що труднощі обробки в основному виникають зі збільшенням розмірів деталей за законом кубічної параболи:
i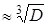 
Тут i - одиниця допуску для номінальних розмірів до 500 мм. D - середньоарифметичний розмір всередині розглянутого інтервалу розмірів.
Так, для 3 мм i = 0.55, а для 500 мм i = 3.89. Тобто величина допуску на виготовлення розміру через i залежить від самого розміру. Для розмірів до 500 мм допуски у квалітетах від 01 до 4 визначені за формулами:
IT 01 = 0.3 +0,008 Ди,
де Ди – середнє геометричне його граничних значень.
IТО = 0,5 + 0,012 Ди
ITI = 0,8 + 0,020 Ди
IT2 = ITI * IТЗ
IТЗ = ITI * IТ3
IТ4=IТЗ * IT5
За цими формулами проводять розрахунок допусків і граничних відхилень для кожного інтервалу номінальних розмірів.
Система допусків та посадок поширюється на розміри до 40000 мм. Вказаний діапазон розбитий на групи:
до 500 мм, 500 - 3150 мм, 3150 - 10000 мм, 10000 -40000 мм - всі вони розбиваються на основні й проміжні інтервали.
Для розмірів до 500 мм установлено 13 основних інтервалів (наприклад: від 10 до 18 мм). Проміжні інтервали введені для відхилень, що утворюють посадки з більшими натягами і зазорами для одержання більш рівномірних зазорів і натягів. Проміжні інтервали починаються з 10 мм (10-14 мм, 14-18 мм).
Система похибок
Величина допуску не зовсім повно характеризує точність обробки.
Основними джерелами появи відхилень заданих розмірів і форми виробу є похибки:
- розмірів;
- геометричної форми;
- взаємного розташування поверхонь;
- пов'язані із чистотою обробки (шорсткості):
Ці 4 групи похибок у процесі виготовлення виникають під дією ряду причин, серед яких слід зазначити:
а)неточність виготовлення устаткування (верстат, прес і т.д.);
б)неточність виготовлення пристосувань для обробки, їхнє зношування;
в)пружні деформації різальних інструментів, їхнє зношування, неточність виготовлення інструмента, температурний вплив;
г)неоднорідність матеріалу, пружні деформації, температурний вплив тощо. Це система технічних похибок;
5 - виміру, включаючи похибки вимірювальних засобів;
6 - залежні від обраної технічної системи й режиму обробки;
7 - коливання припуску на механічну обробку тощо.
Похибки при виготовленні деталей можна поділити на:
1) систематичні постійні (неправильно настроєний верстат);
2) систематичні змінні (зношування інструмента);
3) випадкові похибки.
Якщо систематичні можуть бути виявлені і у ряді випадків усунуті в процесі підготовки виробництва або виготовлення деталей, то виявлення випадкових похибок вимагає вивчення.
Численні досвіди показують, що випадкова похибка виготовлення дуже добре узгоджується із законом нормального розподілу.
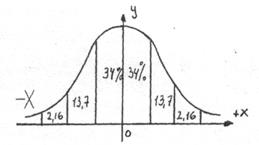
Рис. 2 Крива Гауса
Крива показує, що найбільше число - 68% всіх виготовлених деталей мають похибки, близькі до середнього розміру, 27,4% деталей мають відхилення в межах від 1/3 до 2/3 допуску, і тільки незначна кількість деталей - 4,32% - має розміри, близькі до найменших і найбільших граничних розмірів.
Нехай X - випадкова величина
У- щільність імовірності
σ - середньоквадратичне відхилення X
За законом Гауса:
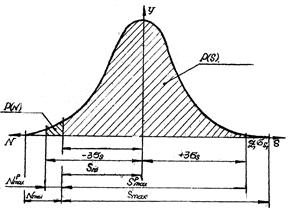
Якщо IT – допуск посадки, то площу, укладену між кривою й віссю X приймають за 1 або за 100%.
Її можна виразити через інтеграл:
, 
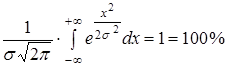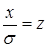, dx=σdz
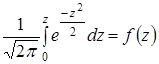
Беремо половину площі:
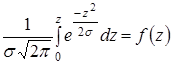- певний інтеграл функції Лапласа. Його можна знайти в будь-якому інженерному довіднику: при z = 3, х = 3σ, 2x = 6σ:
f(3)~0,4987≈0,5
2f(3)≈1=100%
ВИСНОВОК: для похибок, які підкоряються закону Гауса, за зону розсіювання дійсних розмірів, що дорівнює допуску на виготовлення деталей, приймається зона +, -3σ або 6σ. Імовірність цього близька до 100%. Вихід за зону розсіювання становить усього 0.27%.
Приклад: обробляється партія деталей 1000 шт, ІТ- відомий допуск посадки.
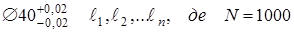
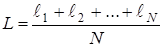
де L - дійсний розмір.
Визначимо так названу залишкову похибку:
X=l1 - L
Згрупуємо дійсні розміри за групами:
40,02 - nl;
40,02-40,01 - n2;
40,01-40,00 – n3;
ni ~ частота появи того самого розміру
Емпірична крива:
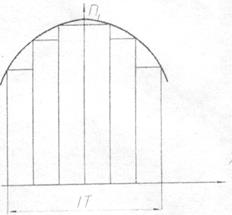
Тобто проводиться селективне складання, наприклад: H7/g6
 |
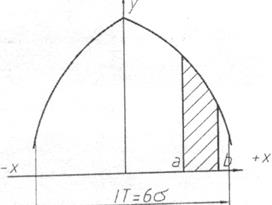Для збільшення точності і однорідності з’єднання деталі сортують на групи з більше вузькими допусками і складання ведуть за цими групами. Цим методом збирають двигуни внутрішнього згоряння, за цим методом працюють шарикопідшипникові заводи.
Додаткові витрати селективного складання окупаються високим cтупенем автоматизації і механізації виробництва.
Питання для самоперевірки:
1. Яка одиниця вимірювання використовується для лінійних вимірювань?
2. Яке відхилення називається основним?
3. Скільки існує квалітетів? Наведіть приклад їх визначення?
4. Наведіть приклади визначення полів допуску на кресленнях.
5. Які причини викликають похибки?
6. Назвіть види похибок.
7. В чому сутність селективного складання?
Лекція №6
Дата: 2019-05-28, просмотров: 296.
