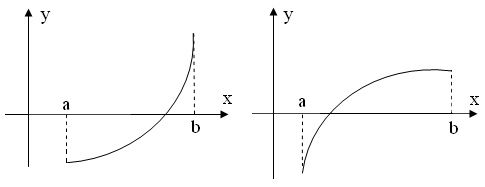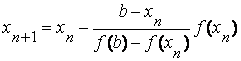1. Матрица симметрична относительно главной диагонали, то есть  .
.
2. Матрица является положительно определенной. Следовательно, при решении методом Гаусса можно воспользоваться схемой единственного деления.
3. Определитель матрицы будет отличен от нуля, если в качестве базиса выбраны линейно независимые функции 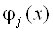 ; в этом случае система (7.18) имеет единственное решение.
; в этом случае система (7.18) имеет единственное решение.
В качестве базисных можно выбрать линейно независимые степенные функции
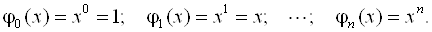 (7.23)
(7.23)
Следует учесть, что N << K. Тогда для этих функций расширенная матрица Грама примет вид
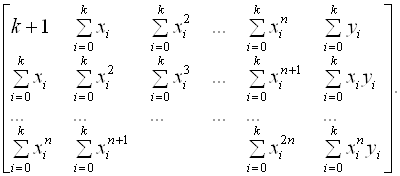 (7.24)
(7.24)
Если выбрать N = K, то на основании единственности интерполяционного полинома получим функцию 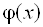 , совпадающую с каноническим интерполяционным полиномом степени K. При этом аппроксимирующая кривая пройдет через все экспериментальные точки, и функция S будет равна нулю.
, совпадающую с каноническим интерполяционным полиномом степени K. При этом аппроксимирующая кривая пройдет через все экспериментальные точки, и функция S будет равна нулю.
ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ
Метод хорд
Пусть на отрезке [ a , b ] функция f ( x ) непрерывна, принимает на концах отрезка значение разных знаков, а производная f ’( x ) сохраняет знак. В зависимости от знака второй производной возможны следующие случаи расположения кривых (рис. 2.7., 2.8):
1.f ( a )<0, f ( b )>0, f ‘( x )>0 – функция возрастает:
| а) f ’’( x )>0 (кривая вогнута вниз) | б) f ’’( x )<0 (кривая вогнута вверх) |
|
| |
Рис. 2.7
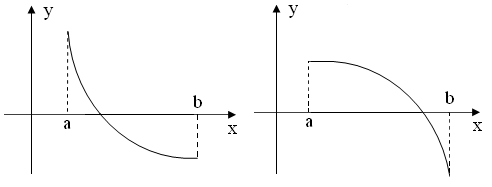
2.f ( a )>0, f ( b )<0, f ‘( x )<0 – функция убывает:
| а) f ’’( x )>0 (кривая вогнута вниз) | б) f ’’( x )<0 (кривая вогнута вверх) |
|
| |
Рис. 2.8
Рассмотрим случай, когда f ’( x ) и f ’’( x ) имеют одинаковые знаки (рис. 2.9.).
3. f ( a )<0, f ( b )>0, f ‘( x )>0 – функция возрастает
а) f ’’( x )>0 (кривая вогнута вниз) б) f ’’( x )<0 (кривая вогнута вверх)
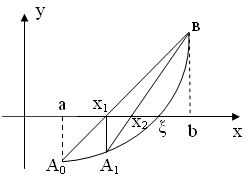
| f(a)<0, f(b)>0 f ‘(x)>0, f ’’(x)>0 |
| Рис. 2.9 |
График функции проходит через точки A 0 ( a , f ( a )) и B ( b , f ( b )). Искомый корень уравнения (точка ξ) нам известен, вместо него возьмем точку x 1 пересечения хорды A 0 B с осью абсцисс это и будет приближенное значение корня.
Уравнение хорды A 0 B:
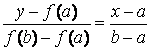
Найдем значение x = x 1, для которого y = 0 :
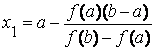
Теперь корень находится на отрезке [ x 1 , b ]. Применим метод хорд к этому отрезку. Проведем хорду, соединяющую точки A 1 ( x 1 , f ( x 1 )) и B и найдем точку x 2 – точку пересечения хорды A 1 B с осью ox
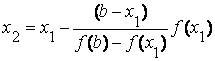
Продолжая этот процесс, находим:
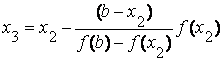
| и т.д. | ||
| | (2.2) | ||
В этом случае конец b отрезка [ a , b ] остается неподвижным, а конец a перемещается.
Формула (2.2) носит название формулы метода хорд. Вычисление по формуле (2.2) продолжаем до тех пор, пока не достигнем заданной точности, т.е. должно выполняться условие:
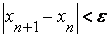
где  - заданная погрешность.
- заданная погрешность.
Теперь рассмотрим случай, когда первая и вторая производные имеют разные знаки, т.е. f ‘( x ) f ’’( x )<0 (рис. 2.10).
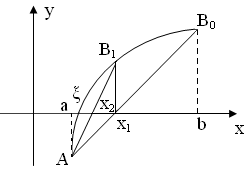
Рис. 2.10
Соединим точки A ( a , f ( a )) и B 0 ( b , f ( b )) хордой AB 0. Точку пересечения хорды AB 0 с осью ox будем считать первым приближением корня. В этом случае, очевидно, неподвижным концом отрезка будет являться конец a.
Запишем уравнение хорды AB 0:
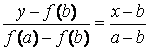
Отсюда найдем x 1, полагая y = 0:
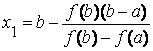
Теперь корень следующий:
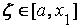
Применяя метод хорд к отрезку, получим
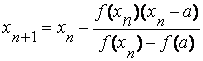
| (2.3) |
Условие окончания вычислений:
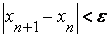
Итак, если f ‘( x ) f ’’( x )>0 приближенное значение корня находят по формуле (2.2), если f ‘( x ) · f ’’( x )<0, то по формуле (2.3).
Практически выбор той или иной формулы осуществляют, пользуясь следующим правилом: неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной.
Оценка погрешности интерполяционной формулы Лагранжа
Имеем yj = f ( xj ), Ln(x). Многочлен Ln(x) построен так, что Ln( xj ) = f ( xj ). Вычисляя погрешность Rn(x) таким образом: Rn(x) = f (x) - Ln(x), можно получить следующую формулу для оценки погрешности интерполяционной формулы Лагранжа: 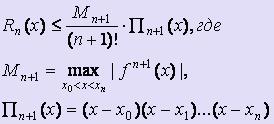 . Такая оценка возможна только в том случае, когда известно аналитическое выражение для f. Если же f задана таблично, то производные заменяются конечными разностями.
. Такая оценка возможна только в том случае, когда известно аналитическое выражение для f. Если же f задана таблично, то производные заменяются конечными разностями.
Интерполяционные формулы Ньютона
- Первая интерполяционная формула Ньютона Пусть yi = f ( xi ), xi = x0 + ih, i = 1, 2, :, n. Нужно построить Pn(x), удовлетворяющий двум условиям:
1. Степень полинома не должна превышать n.
2. Pn( xi ) = yi.
Формула Pn(x) для первой интерполяционной формулы Ньютона имеет вид: 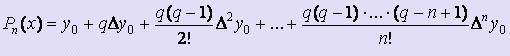 , где q = ( x - x0 ) / h. Первая интерполяционная формула Ньютона применяется тогда, когда x находится вначале таблицы. Тогда в качестве x0 следует брать ближайшее слева к заданному xтабличное значение.
, где q = ( x - x0 ) / h. Первая интерполяционная формула Ньютона применяется тогда, когда x находится вначале таблицы. Тогда в качестве x0 следует брать ближайшее слева к заданному xтабличное значение.
- Вторая интерполяционная формула Ньютона Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую интерполяционную формулу становится невыгодно. Для этого применяется вторая интерполяционная формула Ньютона:
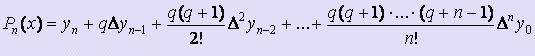 , где q = ( x - xn ) / h. Здесь в качестве xn следует брать ближайшее справа к заданному x табличное значение.
, где q = ( x - xn ) / h. Здесь в качестве xn следует брать ближайшее справа к заданному x табличное значение.
Оценка погрешностей первой и второй интерполяционных формул Ньютона
Используя подстановки q = ( x - x0 ) / h и q = ( x - xn ) / h и заменяя соответствующим образом выражение для Пn+1(x) в формуле оценки погрешности интерполяционной формулы Лагранжа, получим формулы для оценки погрешности интерполирования по первой и второй интерполяционной формуле Ньютона соответственно: 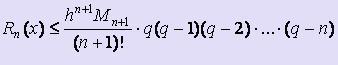 ,
, 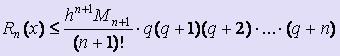 .
.


Метод Эйлера. Усовершенствованный метод Эйлера.
Классический метод Рунге-Кутты
Не обошла стороной вычислительная математика и дифференциальные уравнения! Сегодня на уроке мы познакомимся с основами приближённых вычислений в этом разделе математического анализа, после чего перед вами приветливо распахнутся толстые-претолстые книги по теме. Ибо вычислительная математика стороной диффуры ещё как не обошла =)
Перечисленные в заголовке методы предназначены для приближённого нахождения решений дифференциальных уравнений, систем ДУ, и краткая постановка наиболее распространённой задачи такова:
Рассмотрим дифференциальное уравнение первого порядка 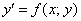 , для которого требуется найти частное решение, соответствующее начальному условию
, для которого требуется найти частное решение, соответствующее начальному условию 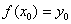 . Что это значит? Это значит, нам нужно найти функцию
. Что это значит? Это значит, нам нужно найти функцию 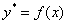 (предполагается её существование), которая удовлетворяет данному дифф. уравнению, и график которой проходит через точку
(предполагается её существование), которая удовлетворяет данному дифф. уравнению, и график которой проходит через точку 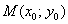 .
.
Но вот незадача – переменные в уравнении 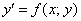 разделить невозможно. Никакими известными науке способами. А если и возможно, то получается неберущийся интеграл. Однако частное-то решение существует! И здесь на помощь приходят методы приближенных вычислений, которые позволяют с высокой (а зачастую с высочайшей) точностью «сымитировать» функцию
разделить невозможно. Никакими известными науке способами. А если и возможно, то получается неберущийся интеграл. Однако частное-то решение существует! И здесь на помощь приходят методы приближенных вычислений, которые позволяют с высокой (а зачастую с высочайшей) точностью «сымитировать» функцию 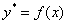 на некотором промежутке.
на некотором промежутке.
Идея методов Эйлера и Рунге-Кутты состоит в том, чтобы заменить фрагмент графика 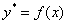 ломаной линией, и сейчас мы узнаем, как эта идея реализуется на практике. И не только узнаем, но и непосредственно реализуем =) Начнём с исторически первого и самого простого метода. …Вы хотите иметь дело со сложным дифференциальным уравнением? Вот и я тоже не хочу:)
ломаной линией, и сейчас мы узнаем, как эта идея реализуется на практике. И не только узнаем, но и непосредственно реализуем =) Начнём с исторически первого и самого простого метода. …Вы хотите иметь дело со сложным дифференциальным уравнением? Вот и я тоже не хочу:)
Задание
Найти частное решение дифференциального уравнения 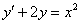 , соответствующее начальному условию
, соответствующее начальному условию 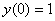 , методом Эйлера на отрезке
, методом Эйлера на отрезке 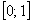 с шагом
с шагом 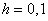 . Построить таблицу и график приближённого решения.
. Построить таблицу и график приближённого решения.
Разбираемся. Во-первых, перед нами обычное линейное уравнение, которое можно решить стандартными способами, и поэтому очень трудно устоять перед соблазном сразу же найти точное решение:
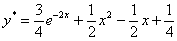 – желающие могут выполнить проверку и убедиться, что данная функция удовлетворяет начальному условию
– желающие могут выполнить проверку и убедиться, что данная функция удовлетворяет начальному условию 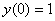 и является корнем уравнения
и является корнем уравнения 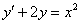 .
.
Что нужно сделать? Нужно найти и построить ломаную, которая приближает график функции 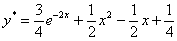 на промежутке
на промежутке 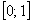 . Поскольку длина этого промежутка равна единице, а шаг составляет
. Поскольку длина этого промежутка равна единице, а шаг составляет 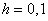 , то наша ломаная будет состоять из 10 отрезков:
, то наша ломаная будет состоять из 10 отрезков:
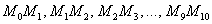
причём, точка 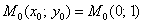 уже известна – она соответствует начальному условию
уже известна – она соответствует начальному условию 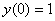 . Кроме того, очевидны «иксовые» координаты других точек:
. Кроме того, очевидны «иксовые» координаты других точек:
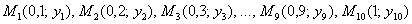
Осталось найти 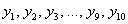 . Никакого дифференцирования и интегрирования – только сложение и умножение! Каждое следующее «игрековое» значение получается из предыдущего по простой рекуррентной формуле:
. Никакого дифференцирования и интегрирования – только сложение и умножение! Каждое следующее «игрековое» значение получается из предыдущего по простой рекуррентной формуле:
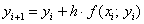
Представим дифференциальное уравнение 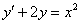 в виде
в виде 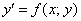 :
:
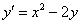
Таким образом: 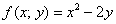
«Раскручиваемся» от начального условия 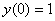 :
:
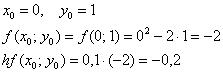
Понеслось:
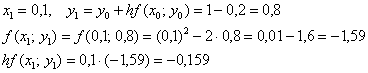
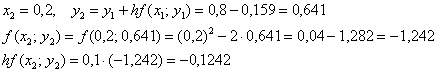
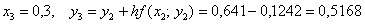
и так далее – до победного конца.
Результаты вычислений удобно заносить в таблицу:
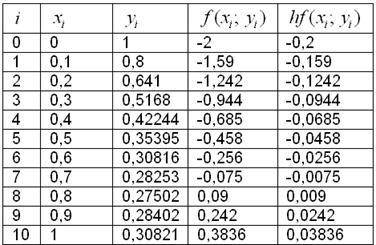
А сами вычисления автоматизировать в Экселе – потому что в математике важен не только победный, но ещё и быстрый конец:)
Дата: 2019-04-23, просмотров: 342.