Имеем yj = f ( xj ), Ln(x). Многочлен Ln(x) построен так, что Ln( xj ) = f ( xj ). Вычисляя погрешность Rn(x) таким образом: Rn(x) = f (x) - Ln(x), можно получить следующую формулу для оценки погрешности интерполяционной формулы Лагранжа: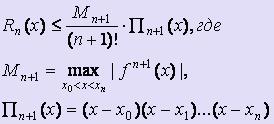 
. Такая оценка возможна только в том случае, когда известно аналитическое выражение для f. Если же f задана таблично, то производные заменяются конечными разностями.
Интерполяционные формулы Ньютона
- Первая интерполяционная формула Ньютона Пусть yi = f ( xi ), xi = x0 + ih, i = 1, 2, :, n. Нужно построить Pn(x), удовлетворяющий двум условиям:
1. Степень полинома не должна превышать n.
2. Pn( xi ) = yi.
Формула Pn(x) для первой интерполяционной формулы Ньютона имеет вид: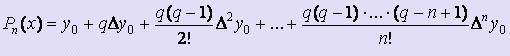 
, где q = ( x - x0 ) / h. Первая интерполяционная формула Ньютона применяется тогда, когда x находится вначале таблицы. Тогда в качестве x0 следует брать ближайшее слева к заданному xтабличное значение.
- Вторая интерполяционная формула Ньютона Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую интерполяционную формулу становится невыгодно. Для этого применяется вторая интерполяционная формула Ньютона:
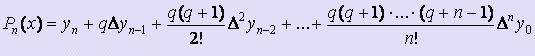, где q = ( x - xn ) / h. Здесь в качестве xn следует брать ближайшее справа к заданному x табличное значение.
Оценка погрешностей первой и второй интерполяционных формул Ньютона
Используя подстановки q = ( x - x0 ) / h и q = ( x - xn ) / h и заменяя соответствующим образом выражение для Пn+1(x) в формуле оценки погрешности интерполяционной формулы Лагранжа, получим формулы для оценки погрешности интерполирования по первой и второй интерполяционной формуле Ньютона соответственно: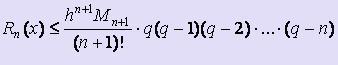 
, 
.
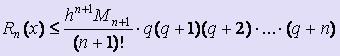Погрешности разные
Оценка погрешности интерполяционной формулы Лагранжа
Имеем yj = f ( xj ), Ln(x). Многочлен Ln(x) построен так, что Ln( xj ) = f ( xj ). Вычисляя погрешность Rn(x) таким образом: Rn(x) = f (x) - Ln(x), можно получить следующую формулу для оценки погрешности интерполяционной формулы Лагранжа: 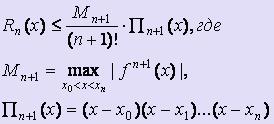. Такая оценка возможна только в том случае, когда известно аналитическое выражение для f. Если же f задана таблично, то производные заменяются конечными разностями.
Интерполяционные формулы Ньютона
- Первая интерполяционная формула Ньютона Пусть yi = f ( xi ), xi = x0 + ih, i = 1, 2, :, n. Нужно построить Pn(x), удовлетворяющий двум условиям:
1. Степень полинома не должна превышать n.
2. Pn( xi ) = yi.
Формула Pn(x) для первой интерполяционной формулы Ньютона имеет вид: 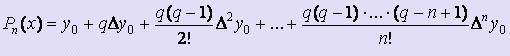, где q = ( x - x0 ) / h. Первая интерполяционная формула Ньютона применяется тогда, когда x находится вначале таблицы. Тогда в качестве x0 следует брать ближайшее слева к заданному xтабличное значение.
- Вторая интерполяционная формула Ньютона Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую интерполяционную формулу становится невыгодно. Для этого применяется вторая интерполяционная формула Ньютона: 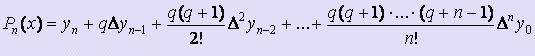, где q = ( x - xn ) / h. Здесь в качестве xn следует брать ближайшее справа к заданному x табличное значение.
Оценка погрешностей первой и второй интерполяционных формул Ньютона
Используя подстановки q = ( x - x0 ) / h и q = ( x - xn ) / h и заменяя соответствующим образом выражение для Пn+1(x) в формуле оценки погрешности интерполяционной формулы Лагранжа, получим формулы для оценки погрешности интерполирования по первой и второй интерполяционной формуле Ньютона соответственно: , .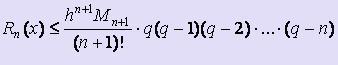
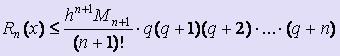21.)
| Отыскание параметров эмпирических формул . методом наименьших квадратов | 
| 
| 
|
При эмпирическом (экспериментальном) изучении функциональной зависимости одной величины У
от другой Х производят ряд измерений величины У при различных значениях величины Х.
Полученные результаты можно представить в виде таблицы, графика:
|
Дата: 2019-04-23, просмотров: 186.
