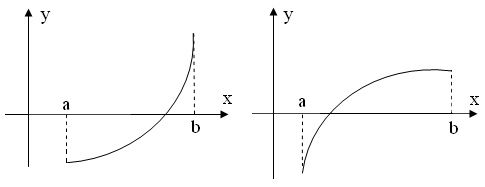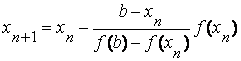В отличие от метода прямоугольников, метод трапеций применим к функциям, заданным в конечном числе точек, так как мы всегда можем взять в качесве узлов интегрирования данные точки.

Числовой пример

Вычислим по формулам прямоугольников и трапеций при 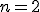интеграл

( 14 )

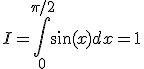
В данном случае

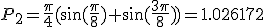
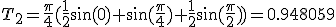
Зная точный ответ (14), найдем погрешности

( 15 )

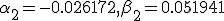
Вторая производная функции 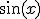на отрезке 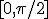отрицательна, ее модуль не превышает единицы: 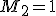. Величина погрешностей (15) удовлетворяет неравенствам (9) и (13):

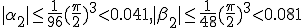
7. 2. ПРИБЛИЖЕННОЕ РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ

Метод хорд

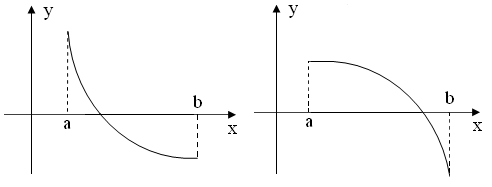
Пусть на отрезке [ a , b ] функция f ( x ) непрерывна, принимает на концах отрезка значение разных знаков, а производная f ’( x ) сохраняет знак. В зависимости от знака второй производной возможны следующие случаи расположения кривых (рис. 2.7., 2.8):

1.f ( a )<0, f ( b )>0, f ‘( x )>0 – функция возрастает:

Рис. 2.7

2.f ( a )>0, f ( b )<0, f ‘( x )<0 – функция убывает:

Рис. 2.8

Рассмотрим случай, когда f ’( x ) и f ’’( x ) имеют одинаковые знаки (рис. 2.9.).

3. f ( a )<0, f ( b )>0, f ‘( x )>0 – функция возрастает

а) f ’’( x )>0 (кривая вогнута вниз) б) f ’’( x )<0 (кривая вогнута вверх)

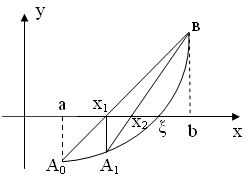
	f(a)<0, f(b)>0 f ‘(x)>0, f ’’(x)>0
Рис. 2.9

График функции проходит через точки A ₀ ( a , f ( a )) и B ( b , f ( b )). Искомый корень уравнения (точка ξ) нам известен, вместо него возьмем точку x ₁ пересечения хорды A ₀ B с осью абсцисс это и будет приближенное значение корня.

Уравнение хорды A ₀ B:

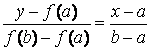
Найдем значение x = x ₁, для которого y = 0 :

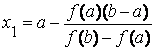
Теперь корень находится на отрезке [ x ₁ , b ]. Применим метод хорд к этому отрезку. Проведем хорду, соединяющую точки A ₁ ( x ₁ , f ( x ₁ )) и B и найдем точку x ₂ – точку пересечения хорды A ₁ B с осью ox

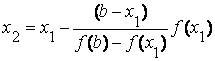
Продолжая этот процесс, находим:

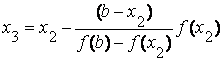
	и т.д.
		(2.2)

В этом случае конец b отрезка [ a , b ] остается неподвижным, а конец a перемещается.

Формула (2.2) носит название формулы метода хорд. Вычисление по формуле (2.2) продолжаем до тех пор, пока не достигнем заданной точности, т.е. должно выполняться условие:

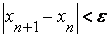
где 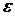- заданная погрешность.

Теперь рассмотрим случай, когда первая и вторая производные имеют разные знаки, т.е. f ‘( x ) f ’’( x )<0 (рис. 2.10).

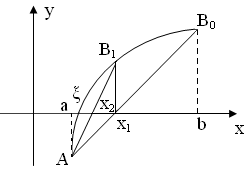
Рис. 2.10

Соединим точки A ( a , f ( a )) и B ₀ ( b , f ( b )) хордой AB ₀. Точку пересечения хорды AB ₀ с осью ox будем считать первым приближением корня. В этом случае, очевидно, неподвижным концом отрезка будет являться конец a.

Запишем уравнение хорды AB ₀:

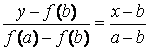
Отсюда найдем x ₁, полагая y = 0:

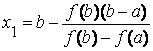
Теперь корень следующий:

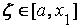
Применяя метод хорд к отрезку, получим

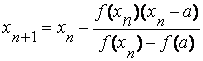
(2.3)

Условие окончания вычислений:

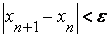
Итак, если f ‘( x ) f ’’( x )>0 приближенное значение корня находят по формуле (2.2), если f ‘( x ) · f ’’( x )<0, то по формуле (2.3).

Практически выбор той или иной формулы осуществляют, пользуясь следующим правилом: неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной.