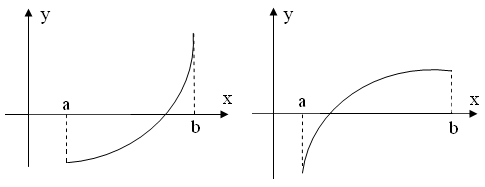Методы Ньютона-Котеса
Метод прямоугольников
Одним из простейших методов численного интегрирования является метод прямоугольников. На частичном отрезке 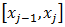 подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка
подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка 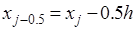 . Тогда значение интеграла на частичном отрезке:
. Тогда значение интеграла на частичном отрезке:
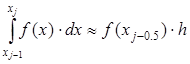 (2.6)
(2.6)
Подставив это выражение в (2.4), получим составную формулу средних прямоугольников:
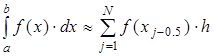 (2.7)
(2.7)
Графическая иллюстрация метода средних прямоугольников представлена на рис.2.2(a). Из рисунка видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы N элементарных прямоугольников.
Формулу (2.7) можно представить в ином виде:
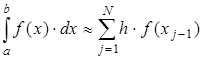 или
или  (2.8)
(2.8)
Эти формулы называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис.2.2(б, в). Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе средних прямоугольников.
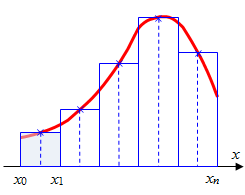 а) средние прямоугольники а) средние прямоугольники
| 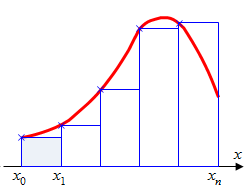 б) левые прямоугольники б) левые прямоугольники
| 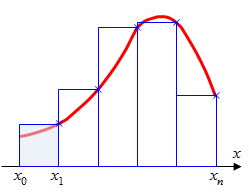 в) правые прямоугольники в) правые прямоугольники
|
| Рис.2.2. Интегрирование методом прямоугольников | ||
Метод трапеций
Если на частичном отрезке 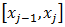 подынтегральную функцию заменить полиномом Лагранжа первой степени:
подынтегральную функцию заменить полиномом Лагранжа первой степени:
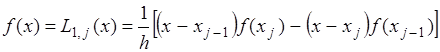 (2.9)
(2.9)
то искомый интеграл на частичном отрезке запишется следующим образом:
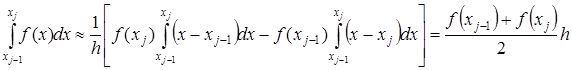 (2.10)
(2.10)
Тогда составная формула трапеций на всем отрезке интегрирования 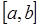 примет вид:
примет вид:
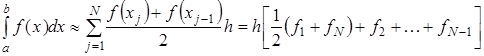 (2.11)
(2.11)
Графически метод трапеций представлен на рис.2.3. Площадь криволинейной трапеции заменяется площадью многоугольника, составленного из Nтрапеций, при этом кривая заменяется вписанной в нее ломаной. На каждом из частичных отрезков функция аппроксимируется прямой, проходящей через конечные значения, при этом площадь трапеции на каждом отрезке определяется по формуле 2.10.
Погрешность метода трапеций выше, чем у метода средних прямоугольников. Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда.
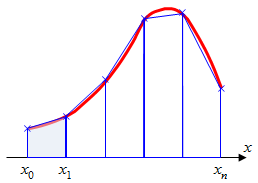
Рис.2.3. Интегрирование методом методом трапеций
Метод Симпсона
В этом методе подынтегральная функция на частичном отрезке 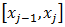 аппроксимируется параболой, проходящей через три точки
аппроксимируется параболой, проходящей через три точки 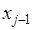 ,
,  ,
, 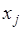 , то есть интерполяционным многочленом Лагранжа второй степени:
, то есть интерполяционным многочленом Лагранжа второй степени:
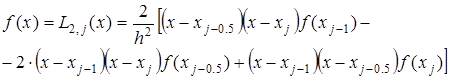 (2.12)
(2.12)
Проведя интегрирование, получим:
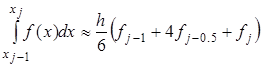 (2.13)
(2.13)
Это и есть формула Симпсона или формула парабол. На отрезке 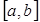 формула Симпсона примет вид:
формула Симпсона примет вид:
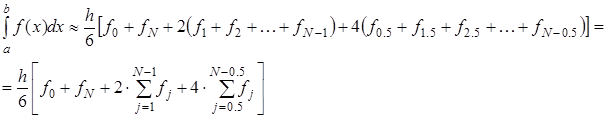 (2.14)
(2.14)
Если разбить отрезок интегрирования 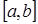 на четное количество 2N равных частей с шагом
на четное количество 2N равных частей с шагом 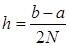 , то можно построить параболу на каждом сдвоенном частичном отрезке
, то можно построить параболу на каждом сдвоенном частичном отрезке 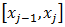 и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
 (2.15)
(2.15)
Графическое представление метода Симпсона показано на рис.2.4. На каждом из сдвоенных частичных отрезков заменяем дугу данной кривой параболой.
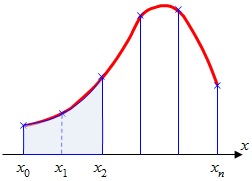
Рис.2.4. Метод Симпсона
Методы Ньютона-Котеса
Метод прямоугольников
Одним из простейших методов численного интегрирования является метод прямоугольников. На частичном отрезке 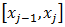 подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка
подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка 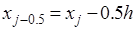 . Тогда значение интеграла на частичном отрезке:
. Тогда значение интеграла на частичном отрезке:
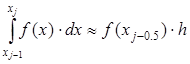 (2.6)
(2.6)
Подставив это выражение в (2.4), получим составную формулу средних прямоугольников:
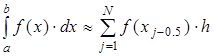 (2.7)
(2.7)
Графическая иллюстрация метода средних прямоугольников представлена на рис.2.2(a). Из рисунка видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы N элементарных прямоугольников.
Формулу (2.7) можно представить в ином виде:
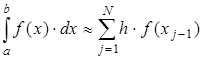 или
или  (2.8)
(2.8)
Эти формулы называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис.2.2(б, в). Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе средних прямоугольников.
 а) средние прямоугольники а) средние прямоугольники
|  б) левые прямоугольники б) левые прямоугольники
|  в) правые прямоугольники в) правые прямоугольники
|
| Рис.2.2. Интегрирование методом прямоугольников | ||
Метод трапеций
Если на частичном отрезке 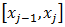 подынтегральную функцию заменить полиномом Лагранжа первой степени:
подынтегральную функцию заменить полиномом Лагранжа первой степени:
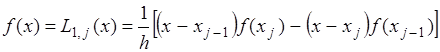 (2.9)
(2.9)
то искомый интеграл на частичном отрезке запишется следующим образом:
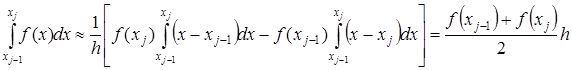 (2.10)
(2.10)
Тогда составная формула трапеций на всем отрезке интегрирования 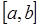 примет вид:
примет вид:
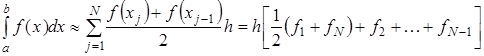 (2.11)
(2.11)
Графически метод трапеций представлен на рис.2.3. Площадь криволинейной трапеции заменяется площадью многоугольника, составленного из Nтрапеций, при этом кривая заменяется вписанной в нее ломаной. На каждом из частичных отрезков функция аппроксимируется прямой, проходящей через конечные значения, при этом площадь трапеции на каждом отрезке определяется по формуле 2.10.
Погрешность метода трапеций выше, чем у метода средних прямоугольников. Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда.

Рис.2.3. Интегрирование методом методом трапеций
Метод Симпсона
В этом методе подынтегральная функция на частичном отрезке 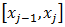 аппроксимируется параболой, проходящей через три точки
аппроксимируется параболой, проходящей через три точки 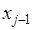 ,
,  ,
, 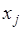 , то есть интерполяционным многочленом Лагранжа второй степени:
, то есть интерполяционным многочленом Лагранжа второй степени:
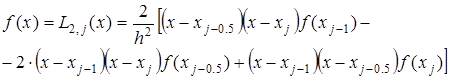 (2.12)
(2.12)
Проведя интегрирование, получим:
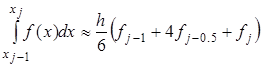 (2.13)
(2.13)
Это и есть формула Симпсона или формула парабол. На отрезке 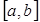 формула Симпсона примет вид:
формула Симпсона примет вид:
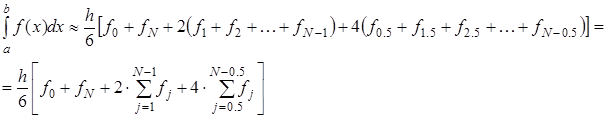 (2.14)
(2.14)
Если разбить отрезок интегрирования 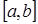 на четное количество 2N равных частей с шагом
на четное количество 2N равных частей с шагом 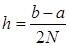 , то можно построить параболу на каждом сдвоенном частичном отрезке
, то можно построить параболу на каждом сдвоенном частичном отрезке 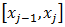 и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
 (2.15)
(2.15)
Графическое представление метода Симпсона показано на рис.2.4. На каждом из сдвоенных частичных отрезков заменяем дугу данной кривой параболой.

Рис.2.4. Метод Симпсона
Метод Зейделя
Метод Зейделя (иногда называемый методом Гаусса-Зейделя) является модификацией метода простой итерации, заключающейся в том, что при вычислении очередного приближения x(k+1) (см. формулы (1.13),(1.14)) его уже полученные компоненты x1(k+1), ...,xi - 1(k+1) сразу же используются для вычисления xi(k+1).
В координатной форме записи метод Зейделя имеет вид:
x1(k+1) = c11x1(k) + c12x2(k) + ... + c1n-1xn-1(k) + c1nxn(k) + d1
x2(k+1) = c21x1(k+1) + c22x2(k) + ... + c2n-1xn-1(k) + c2nxn(k) + d2
...
xn(k+1) = cn1x1(k+1) + cn2x2(k+1) + ... + cnn-1xn-1(k+1) + cnnxn(k) + dn
где x(0) - некоторое начальное приближение к решению.
Таким образом i-тая компонента (k+1)-го приближения вычисляется по формуле
| xi(k+1) = ∑ j=1i-1 cijxj(k+1) + ∑ nj=i cijxj(k) + di , i = 1, ..., n | (1.20) |
Условие окончания итерационного процесса Зейделя при достижении точности ε в упрощенной форме имеет вид:
|| x (k+1) - x (k) || ≤ ε.
Существует более точное условие окончания итерационного процесса, которое более сложно и требует дополнительных вычислений (см., например, [1, стр.327]).
3. Метод хорд
Пусть f(a)f(b)<0. Сущность метода (его еще называют методом ложного положения) состоит в замене кривой y=f(x) хордами, проходящими через концы отрезков, в которых f(x) имеет противоположные знаки. Метод хорд требует, чтобы один конец отрезка, на котором ищется корень, был неподвижен. В качестве неподвижного конца х0 выбирают тот конец отрезка, для которого знак f(x) совпадает со знаком второй производной 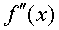 . Расчетная формула имеет вид
. Расчетная формула имеет вид
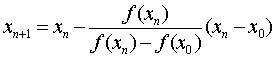
Метод хорд является двухточечным, его сходимость монотонная и односторонняя.
4. Метод Логранджа
Многочлен Лагранжа
При глобальной интерполяции на всем интервале 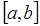 строится единый многочлен. Одной из форм записи интерполяционного многочлена для глобальной интерполяции является многочлен Лагранжа:
строится единый многочлен. Одной из форм записи интерполяционного многочлена для глобальной интерполяции является многочлен Лагранжа:
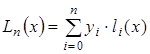 (3.11)
(3.11)
где 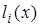 – базисные многочлены степени n:
– базисные многочлены степени n:
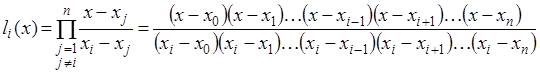 (3.12)
(3.12)
То есть многочлен Лагранжа можно записать в виде:
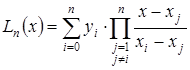 (3.13)
(3.13)
Многочлен 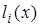 удовлетворяет условию
удовлетворяет условию 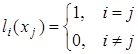 . Это условие означает, что многочлен равен нулю при каждом
. Это условие означает, что многочлен равен нулю при каждом 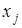 кроме
кроме 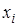 , то есть
, то есть  – корни этого многочлена. Таким образом, степень многочлена
– корни этого многочлена. Таким образом, степень многочлена  равна n и при
равна n и при 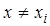 обращаются в ноль все слагаемые суммы, кроме слагаемого с номером
обращаются в ноль все слагаемые суммы, кроме слагаемого с номером 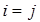 , равного
, равного 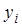 .
.
Выражение (3.11) применимо как для равноотстоящих, так и для не равноотстоящих узлов. Погрешность интерполяции методом Лагранжа зависит от свойств функции  , от расположения узлов интерполяции и точки x. Полином Лагранжа имеет малую погрешность при небольших значениях n (n<20). При больших n погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (то есть его погрешность не убывает с ростом n).
, от расположения узлов интерполяции и точки x. Полином Лагранжа имеет малую погрешность при небольших значениях n (n<20). При больших n погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (то есть его погрешность не убывает с ростом n).
Многочлен Лагранжа в явном виде содержит значения функций в узлах интерполяции, поэтому он удобен, когда значения функций меняются, а узлы интерполяции неизменны. Число арифметических операции, необходимых для построения многочлена Лагранжа, пропорционально 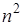 и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что с изменением числа узлов приходится все вычисления проводить заново.
и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что с изменением числа узлов приходится все вычисления проводить заново.
Кусочно-линейная и кусочно-квадратичная локальные интерполяции являются частными случаями интерполяции многочленом Лагранжа.
Многочлен Ньютона
Другая форма записи интерполяционного многочлена – интерполяционный многочлен Ньютона с разделенными разностями. Пусть функция  задана с произвольным шагом, и точки таблицы значений пронумерованы в произвольном порядке.
задана с произвольным шагом, и точки таблицы значений пронумерованы в произвольном порядке.
Разделенные разности нулевого порядка совпадают со значениями функции в узлах. Разделенные разности первого порядка определяются через разделенные разности нулевого порядка:
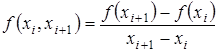 (3.14)
(3.14)
Разделенные разности второго порядка определяются через разделенные разности первого порядка:
 (3.15)
(3.15)
Разделенные разности k-го порядка определяются через разделенные разности порядка 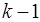 :
:
 (3.16)
(3.16)
Используя понятие разделенной разности интерполяционный многочлен Ньютона можно записать в следующем виде:

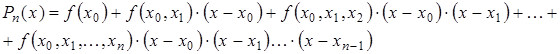 (3.17)
(3.17)
За точностью расчета можно следить по убыванию членов суммы (3.17). Если функция достаточно гладкая, то справедливо приближенное равенство  . Это приближенное равенство можно использовать для практической оценки погрешности интерполяции:
. Это приближенное равенство можно использовать для практической оценки погрешности интерполяции: 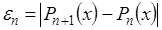 .
.
4. Метод Эйлера
Рассмотрим дифференциальное уравнение
 (1)
(1)
с начальным условием

Подставив 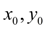 в уравнение (1), получим значение производной в точке
в уравнение (1), получим значение производной в точке  :
:
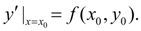
При малом 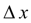 имеет место:
имеет место:
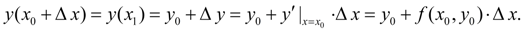
Обозначив 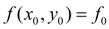 , перепишем последнее равенство в виде:
, перепишем последнее равенство в виде:
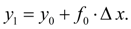 (2)
(2)
Принимая теперь 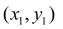 за новую исходную точку, точно также получим:
за новую исходную точку, точно также получим:
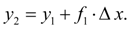
В общем случае будем иметь:
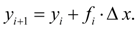 (3)
(3)
Это и есть метод Эйлера. Величина 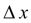 называется шагом интегрирования. Пользуясь этим методом, мы получаем приближенные значения у , так как производная
называется шагом интегрирования. Пользуясь этим методом, мы получаем приближенные значения у , так как производная 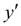 на самом деле не остается постоянной на промежутке длиной
на самом деле не остается постоянной на промежутке длиной 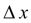 . Поэтому мы получаем ошибку в определении значения функции у , тем большую, чем больше
. Поэтому мы получаем ошибку в определении значения функции у , тем большую, чем больше 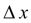 . Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок.
. Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок.
Более точным является модифицированный метод Эйлера с пересчетом. Его суть в том, что сначала по формуле (3) находят так называемое «грубое приближение» (прогноз):
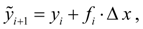
а затем пересчетом 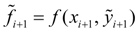 получают тоже приближенное, но более точное значение (коррекция):
получают тоже приближенное, но более точное значение (коррекция):
 (4)
(4)
Фактически пересчет позволяет учесть, хоть и приблизительно, изменение производной 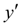 на шаге интегрирования
на шаге интегрирования 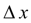 , так как учитываются ее значения
, так как учитываются ее значения 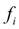 в начале и
в начале и 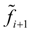 в конце шага (рис. 1), а затем берется их среднее. Метод Эйлера с пересчетом (4) является по существу методом Рунге-Кутта 2-го порядка [2], что станет очевидным из дальнейшего.
в конце шага (рис. 1), а затем берется их среднее. Метод Эйлера с пересчетом (4) является по существу методом Рунге-Кутта 2-го порядка [2], что станет очевидным из дальнейшего.
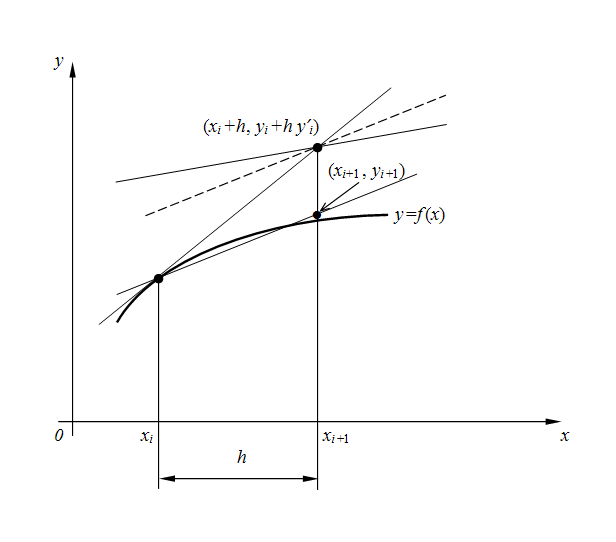
Рис. 1. Геометрическое представление метода Эйлера с пересчетом.
Метод простой итерации
Метод прямоугольников
Метод хорд
Пусть на отрезке [ a , b ] функция f ( x ) непрерывна, принимает на концах отрезка значение разных знаков, а производная f ’( x ) сохраняет знак. В зависимости от знака второй производной возможны следующие случаи расположения кривых (рис. 2.7., 2.8):
1.f ( a )<0, f ( b )>0, f ‘( x )>0 – функция возрастает:
| а) f ’’( x )>0 (кривая вогнута вниз) | б) f ’’( x )<0 (кривая вогнута вверх) |
|
| |
Рис. 2.7
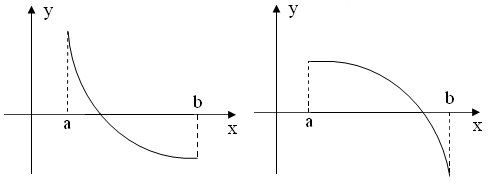
2.f ( a )>0, f ( b )<0, f ‘( x )<0 – функция убывает:
| а) f ’’( x )>0 (кривая вогнута вниз) | б) f ’’( x )<0 (кривая вогнута вверх) |
|
| |
Рис. 2.8
Рассмотрим случай, когда f ’( x ) и f ’’( x ) имеют одинаковые знаки (рис. 2.9.).
3. f ( a )<0, f ( b )>0, f ‘( x )>0 – функция возрастает
а) f ’’( x )>0 (кривая вогнута вниз) б) f ’’( x )<0 (кривая вогнута вверх)
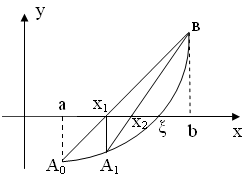
| f(a)<0, f(b)>0 f ‘(x)>0, f ’’(x)>0 |
| Рис. 2.9 |
График функции проходит через точки A 0 ( a , f ( a )) и B ( b , f ( b )). Искомый корень уравнения (точка ξ) нам известен, вместо него возьмем точку x 1 пересечения хорды A 0 B с осью абсцисс это и будет приближенное значение корня.
Уравнение хорды A 0 B:
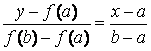
Найдем значение x = x 1, для которого y = 0 :
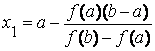
Теперь корень находится на отрезке [ x 1 , b ]. Применим метод хорд к этому отрезку. Проведем хорду, соединяющую точки A 1 ( x 1 , f ( x 1 )) и B и найдем точку x 2 – точку пересечения хорды A 1 B с осью ox
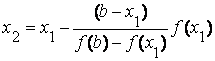
Продолжая этот процесс, находим:
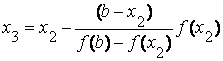
| и т.д. | ||
| | (2.2) | ||
В этом случае конец b отрезка [ a , b ] остается неподвижным, а конец a перемещается.
Формула (2.2) носит название формулы метода хорд. Вычисление по формуле (2.2) продолжаем до тех пор, пока не достигнем заданной точности, т.е. должно выполняться условие:
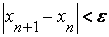
где 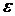 - заданная погрешность.
- заданная погрешность.
Теперь рассмотрим случай, когда первая и вторая производные имеют разные знаки, т.е. f ‘( x ) f ’’( x )<0 (рис. 2.10).
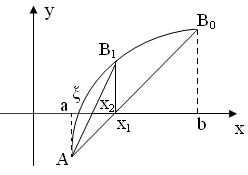
Рис. 2.10
Соединим точки A ( a , f ( a )) и B 0 ( b , f ( b )) хордой AB 0. Точку пересечения хорды AB 0 с осью ox будем считать первым приближением корня. В этом случае, очевидно, неподвижным концом отрезка будет являться конец a.
Запишем уравнение хорды AB 0:
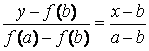
Отсюда найдем x 1, полагая y = 0:
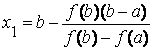
Теперь корень следующий:
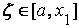
Применяя метод хорд к отрезку, получим
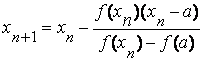
| (2.3) |
Условие окончания вычислений:
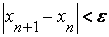
Итак, если f ‘( x ) f ’’( x )>0 приближенное значение корня находят по формуле (2.2), если f ‘( x ) · f ’’( x )<0, то по формуле (2.3).
Практически выбор той или иной формулы осуществляют, пользуясь следующим правилом: неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной.
21.)
| Отыскание параметров эмпирических формул . методом наименьших квадратов | 
| 
| 
|
При эмпирическом (экспериментальном) изучении функциональной зависимости одной величины У
от другой Х производят ряд измерений величины У при различных значениях величины Х.
Полученные результаты можно представить в виде таблицы, графика:
|
Метод хорд
Пусть на отрезке [ a , b ] функция f ( x ) непрерывна, принимает на концах отрезка значение разных знаков, а производная f ’( x ) сохраняет знак. В зависимости от знака второй производной возможны следующие случаи расположения кривых (рис. 2.7., 2.8):
1.f ( a )<0, f ( b )>0, f ‘( x )>0 – функция возрастает:
| а) f ’’( x )>0 (кривая вогнута вниз) | б) f ’’( x )<0 (кривая вогнута вверх) |
|
| |
Рис. 2.7
2.f ( a )>0, f ( b )<0, f ‘( x )<0 – функция убывает:
| а) f ’’( x )>0 (кривая вогнута вниз) | б) f ’’( x )<0 (кривая вогнута вверх) |
|
| |
Рис. 2.8
Рассмотрим случай, когда f ’( x ) и f ’’( x ) имеют одинаковые знаки (рис. 2.9.).
3. f ( a )<0, f ( b )>0, f ‘( x )>0 – функция возрастает
а) f ’’( x )>0 (кривая вогнута вниз) б) f ’’( x )<0 (кривая вогнута вверх)

| f(a)<0, f(b)>0 f ‘(x)>0, f ’’(x)>0 |
| Рис. 2.9 |
График функции проходит через точки A 0 ( a , f ( a )) и B ( b , f ( b )). Искомый корень уравнения (точка ξ) нам известен, вместо него возьмем точку x 1 пересечения хорды A 0 B с осью абсцисс это и будет приближенное значение корня.
Уравнение хорды A 0 B:
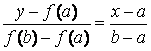
Найдем значение x = x 1, для которого y = 0 :
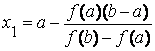
Теперь корень находится на отрезке [ x 1 , b ]. Применим метод хорд к этому отрезку. Проведем хорду, соединяющую точки A 1 ( x 1 , f ( x 1 )) и B и найдем точку x 2 – точку пересечения хорды A 1 B с осью ox
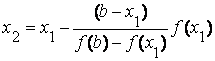
Продолжая этот процесс, находим:
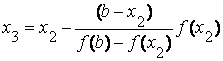
| и т.д. | ||
| | (2.2) | ||
В этом случае конец b отрезка [ a , b ] остается неподвижным, а конец a перемещается.
Формула (2.2) носит название формулы метода хорд. Вычисление по формуле (2.2) продолжаем до тех пор, пока не достигнем заданной точности, т.е. должно выполняться условие:
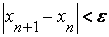
где 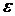 - заданная погрешность.
- заданная погрешность.
Теперь рассмотрим случай, когда первая и вторая производные имеют разные знаки, т.е. f ‘( x ) f ’’( x )<0 (рис. 2.10).

Рис. 2.10
Соединим точки A ( a , f ( a )) и B 0 ( b , f ( b )) хордой AB 0. Точку пересечения хорды AB 0 с осью ox будем считать первым приближением корня. В этом случае, очевидно, неподвижным концом отрезка будет являться конец a.
Запишем уравнение хорды AB 0:
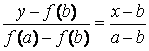
Отсюда найдем x 1, полагая y = 0:
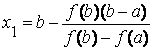
Теперь корень следующий:
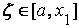
Применяя метод хорд к отрезку, получим
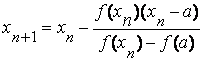
| (2.3) |
Условие окончания вычислений:
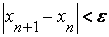
Итак, если f ‘( x ) f ’’( x )>0 приближенное значение корня находят по формуле (2.2), если f ‘( x ) · f ’’( x )<0, то по формуле (2.3).
Практически выбор той или иной формулы осуществляют, пользуясь следующим правилом: неподвижным концом отрезка является тот, для которого знак функции совпадает со знаком второй производной.
Оценка погрешности интерполяционной формулы Лагранжа
Имеем yj = f ( xj ), Ln(x). Многочлен Ln(x) построен так, что Ln( xj ) = f ( xj ). Вычисляя погрешность Rn(x) таким образом: Rn(x) = f (x) - Ln(x), можно получить следующую формулу для оценки погрешности интерполяционной формулы Лагранжа: 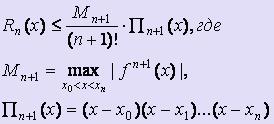 . Такая оценка возможна только в том случае, когда известно аналитическое выражение для f. Если же f задана таблично, то производные заменяются конечными разностями.
. Такая оценка возможна только в том случае, когда известно аналитическое выражение для f. Если же f задана таблично, то производные заменяются конечными разностями.
Интерполяционные формулы Ньютона
- Первая интерполяционная формула Ньютона Пусть yi = f ( xi ), xi = x0 + ih, i = 1, 2, :, n. Нужно построить Pn(x), удовлетворяющий двум условиям:
1. Степень полинома не должна превышать n.
2. Pn( xi ) = yi.
Формула Pn(x) для первой интерполяционной формулы Ньютона имеет вид: 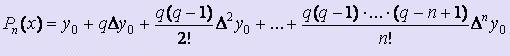 , где q = ( x - x0 ) / h. Первая интерполяционная формула Ньютона применяется тогда, когда x находится вначале таблицы. Тогда в качестве x0 следует брать ближайшее слева к заданному xтабличное значение.
, где q = ( x - x0 ) / h. Первая интерполяционная формула Ньютона применяется тогда, когда x находится вначале таблицы. Тогда в качестве x0 следует брать ближайшее слева к заданному xтабличное значение.
- Вторая интерполяционная формула Ньютона Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую интерполяционную формулу становится невыгодно. Для этого применяется вторая интерполяционная формула Ньютона:
 , где q = ( x - xn ) / h. Здесь в качестве xn следует брать ближайшее справа к заданному x табличное значение.
, где q = ( x - xn ) / h. Здесь в качестве xn следует брать ближайшее справа к заданному x табличное значение.
Оценка погрешностей первой и второй интерполяционных формул Ньютона
Используя подстановки q = ( x - x0 ) / h и q = ( x - xn ) / h и заменяя соответствующим образом выражение для Пn+1(x) в формуле оценки погрешности интерполяционной формулы Лагранжа, получим формулы для оценки погрешности интерполирования по первой и второй интерполяционной формуле Ньютона соответственно:  ,
, 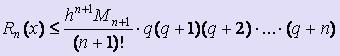 .
.


Метод Эйлера. Усовершенствованный метод Эйлера.
Классический метод Рунге-Кутты
Не обошла стороной вычислительная математика и дифференциальные уравнения! Сегодня на уроке мы познакомимся с основами приближённых вычислений в этом разделе математического анализа, после чего перед вами приветливо распахнутся толстые-претолстые книги по теме. Ибо вычислительная математика стороной диффуры ещё как не обошла =)
Перечисленные в заголовке методы предназначены для приближённого нахождения решений дифференциальных уравнений, систем ДУ, и краткая постановка наиболее распространённой задачи такова:
Рассмотрим дифференциальное уравнение первого порядка 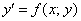 , для которого требуется найти частное решение, соответствующее начальному условию
, для которого требуется найти частное решение, соответствующее начальному условию 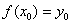 . Что это значит? Это значит, нам нужно найти функцию
. Что это значит? Это значит, нам нужно найти функцию 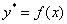 (предполагается её существование), которая удовлетворяет данному дифф. уравнению, и график которой проходит через точку
(предполагается её существование), которая удовлетворяет данному дифф. уравнению, и график которой проходит через точку  .
.
Но вот незадача – переменные в уравнении 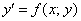 разделить невозможно. Никакими известными науке способами. А если и возможно, то получается неберущийся интеграл. Однако частное-то решение существует! И здесь на помощь приходят методы приближенных вычислений, которые позволяют с высокой (а зачастую с высочайшей) точностью «сымитировать» функцию
разделить невозможно. Никакими известными науке способами. А если и возможно, то получается неберущийся интеграл. Однако частное-то решение существует! И здесь на помощь приходят методы приближенных вычислений, которые позволяют с высокой (а зачастую с высочайшей) точностью «сымитировать» функцию 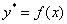 на некотором промежутке.
на некотором промежутке.
Идея методов Эйлера и Рунге-Кутты состоит в том, чтобы заменить фрагмент графика 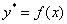 ломаной линией, и сейчас мы узнаем, как эта идея реализуется на практике. И не только узнаем, но и непосредственно реализуем =) Начнём с исторически первого и самого простого метода. …Вы хотите иметь дело со сложным дифференциальным уравнением? Вот и я тоже не хочу:)
ломаной линией, и сейчас мы узнаем, как эта идея реализуется на практике. И не только узнаем, но и непосредственно реализуем =) Начнём с исторически первого и самого простого метода. …Вы хотите иметь дело со сложным дифференциальным уравнением? Вот и я тоже не хочу:)
Задание
Найти частное решение дифференциального уравнения 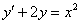 , соответствующее начальному условию
, соответствующее начальному условию  , методом Эйлера на отрезке
, методом Эйлера на отрезке 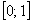 с шагом
с шагом 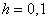 . Построить таблицу и график приближённого решения.
. Построить таблицу и график приближённого решения.
Разбираемся. Во-первых, перед нами обычное линейное уравнение, которое можно решить стандартными способами, и поэтому очень трудно устоять перед соблазном сразу же найти точное решение:
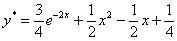 – желающие могут выполнить проверку и убедиться, что данная функция удовлетворяет начальному условию
– желающие могут выполнить проверку и убедиться, что данная функция удовлетворяет начальному условию  и является корнем уравнения
и является корнем уравнения 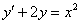 .
.
Что нужно сделать? Нужно найти и построить ломаную, которая приближает график функции 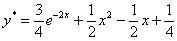 на промежутке
на промежутке 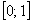 . Поскольку длина этого промежутка равна единице, а шаг составляет
. Поскольку длина этого промежутка равна единице, а шаг составляет 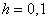 , то наша ломаная будет состоять из 10 отрезков:
, то наша ломаная будет состоять из 10 отрезков:
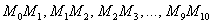
причём, точка  уже известна – она соответствует начальному условию
уже известна – она соответствует начальному условию  . Кроме того, очевидны «иксовые» координаты других точек:
. Кроме того, очевидны «иксовые» координаты других точек:
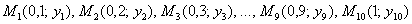
Осталось найти 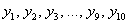 . Никакого дифференцирования и интегрирования – только сложение и умножение! Каждое следующее «игрековое» значение получается из предыдущего по простой рекуррентной формуле:
. Никакого дифференцирования и интегрирования – только сложение и умножение! Каждое следующее «игрековое» значение получается из предыдущего по простой рекуррентной формуле:
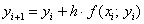
Представим дифференциальное уравнение 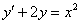 в виде
в виде 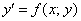 :
:

Таким образом: 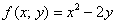
«Раскручиваемся» от начального условия  :
:
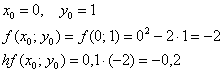
Понеслось:
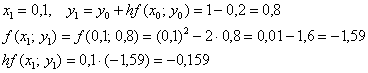
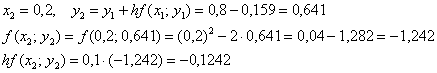
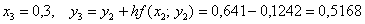
и так далее – до победного конца.
Результаты вычислений удобно заносить в таблицу:
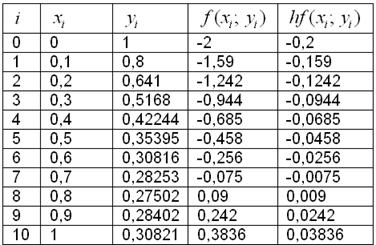
А сами вычисления автоматизировать в Экселе – потому что в математике важен не только победный, но ещё и быстрый конец:)
Методы Ньютона-Котеса
Метод прямоугольников
Одним из простейших методов численного интегрирования является метод прямоугольников. На частичном отрезке 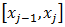 подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка
подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка 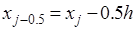 . Тогда значение интеграла на частичном отрезке:
. Тогда значение интеграла на частичном отрезке:
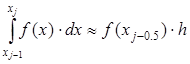 (2.6)
(2.6)
Подставив это выражение в (2.4), получим составную формулу средних прямоугольников:
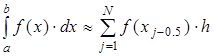 (2.7)
(2.7)
Графическая иллюстрация метода средних прямоугольников представлена на рис.2.2(a). Из рисунка видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы N элементарных прямоугольников.
Формулу (2.7) можно представить в ином виде:
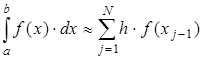 или
или  (2.8)
(2.8)
Эти формулы называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис.2.2(б, в). Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе средних прямоугольников.
 а) средние прямоугольники а) средние прямоугольники
|  б) левые прямоугольники б) левые прямоугольники
|  в) правые прямоугольники в) правые прямоугольники
|
| Рис.2.2. Интегрирование методом прямоугольников | ||
Метод трапеций
Если на частичном отрезке 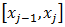 подынтегральную функцию заменить полиномом Лагранжа первой степени:
подынтегральную функцию заменить полиномом Лагранжа первой степени:
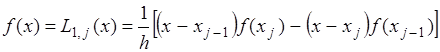 (2.9)
(2.9)
то искомый интеграл на частичном отрезке запишется следующим образом:
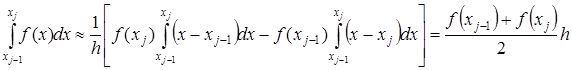 (2.10)
(2.10)
Тогда составная формула трапеций на всем отрезке интегрирования 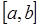 примет вид:
примет вид:
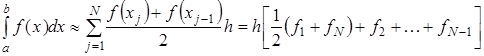 (2.11)
(2.11)
Графически метод трапеций представлен на рис.2.3. Площадь криволинейной трапеции заменяется площадью многоугольника, составленного из Nтрапеций, при этом кривая заменяется вписанной в нее ломаной. На каждом из частичных отрезков функция аппроксимируется прямой, проходящей через конечные значения, при этом площадь трапеции на каждом отрезке определяется по формуле 2.10.
Погрешность метода трапеций выше, чем у метода средних прямоугольников. Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда.

Рис.2.3. Интегрирование методом методом трапеций
Метод Симпсона
В этом методе подынтегральная функция на частичном отрезке 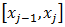 аппроксимируется параболой, проходящей через три точки
аппроксимируется параболой, проходящей через три точки 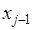 ,
,  ,
, 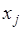 , то есть интерполяционным многочленом Лагранжа второй степени:
, то есть интерполяционным многочленом Лагранжа второй степени:
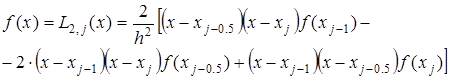 (2.12)
(2.12)
Проведя интегрирование, получим:
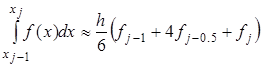 (2.13)
(2.13)
Это и есть формула Симпсона или формула парабол. На отрезке 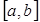 формула Симпсона примет вид:
формула Симпсона примет вид:
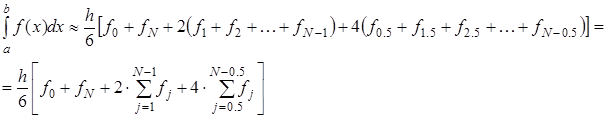 (2.14)
(2.14)
Если разбить отрезок интегрирования 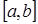 на четное количество 2N равных частей с шагом
на четное количество 2N равных частей с шагом 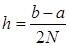 , то можно построить параболу на каждом сдвоенном частичном отрезке
, то можно построить параболу на каждом сдвоенном частичном отрезке 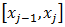 и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
 (2.15)
(2.15)
Графическое представление метода Симпсона показано на рис.2.4. На каждом из сдвоенных частичных отрезков заменяем дугу данной кривой параболой.

Рис.2.4. Метод Симпсона
Семейство методов Ньютона-Котеса
Выше были рассмотрены три схожих метода интегрирования функций – метод прямоугольников, метод трапеций, метод Симпсона. Их объединяет общая идея: интегрируемая функция интерполируется на отрезке интегрирования по равноотстоящим узлам многочленом Лагранжа, для которого аналитически вычисляется значение интеграла. Семейство методов, основанных на таком подходе, называется методами Ньютона-Котеса.
В выражении  коэффициенты
коэффициенты 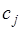 правильнее называть весовыми коэффициентами. Величину
правильнее называть весовыми коэффициентами. Величину 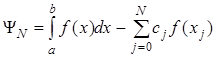 , определяющую погрешность численного интегрирования, называют остатком.
, определяющую погрешность численного интегрирования, называют остатком.
Для семейства методов Ньютона-Котеса можно записать общее выражение:
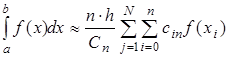 (2.16)
(2.16)
где n – порядок метода Ньютона-Котеса, N – количество частичных отрезков,  ,
, 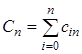 ,
, 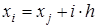 .
.
Из выражения (2.16) легко можно получить формулу прямоугольников для 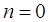 , формулу трапеций для
, формулу трапеций для 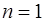 , и формулу Симпсона для
, и формулу Симпсона для  . Коэффициенты
. Коэффициенты 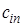 могут быть заданы в табличной форме (таблица.2.1).
могут быть заданы в табличной форме (таблица.2.1).
| n | 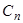
| 
| 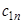
| 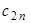
| 
| 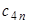
| 
|
| 0 | 1 | 1 | |||||
| 1 | 2 | 1 | 1 | ||||
| 2 | 6 | 1 | 4 | 1 | |||
| 3 | 8 | 1 | 3 | 3 | 1 | ||
| 4 | 90 | 7 | 32 | 12 | 32 | 7 | |
| 5 | 288 | 19 | 75 | 50 | 50 | 75 | 19 |
Таблица 2.1. Весовые коэффициенты метода Ньютона-Котеса
Методы Ньютона-Котеса
Метод прямоугольников
Одним из простейших методов численного интегрирования является метод прямоугольников. На частичном отрезке 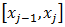 подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка
подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину частичного отрезка 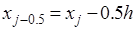 . Тогда значение интеграла на частичном отрезке:
. Тогда значение интеграла на частичном отрезке:
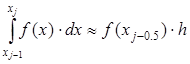 (2.6)
(2.6)
Подставив это выражение в (2.4), получим составную формулу средних прямоугольников:
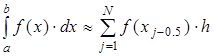 (2.7)
(2.7)
Графическая иллюстрация метода средних прямоугольников представлена на рис.2.2(a). Из рисунка видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы N элементарных прямоугольников.
Формулу (2.7) можно представить в ином виде:
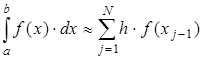 или
или  (2.8)
(2.8)
Эти формулы называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников представлен на рис.2.2(б, в). Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе средних прямоугольников.
 а) средние прямоугольники а) средние прямоугольники
|  б) левые прямоугольники б) левые прямоугольники
|  в) правые прямоугольники в) правые прямоугольники
|
| Рис.2.2. Интегрирование методом прямоугольников | ||
Метод трапеций
Если на частичном отрезке 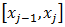 подынтегральную функцию заменить полиномом Лагранжа первой степени:
подынтегральную функцию заменить полиномом Лагранжа первой степени:
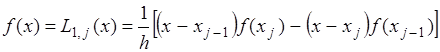 (2.9)
(2.9)
то искомый интеграл на частичном отрезке запишется следующим образом:
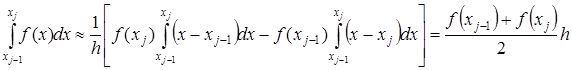 (2.10)
(2.10)
Тогда составная формула трапеций на всем отрезке интегрирования 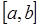 примет вид:
примет вид:
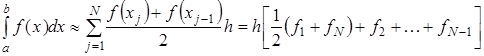 (2.11)
(2.11)
Графически метод трапеций представлен на рис.2.3. Площадь криволинейной трапеции заменяется площадью многоугольника, составленного из Nтрапеций, при этом кривая заменяется вписанной в нее ломаной. На каждом из частичных отрезков функция аппроксимируется прямой, проходящей через конечные значения, при этом площадь трапеции на каждом отрезке определяется по формуле 2.10.
Погрешность метода трапеций выше, чем у метода средних прямоугольников. Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда.

Рис.2.3. Интегрирование методом методом трапеций
Метод Симпсона
В этом методе подынтегральная функция на частичном отрезке 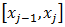 аппроксимируется параболой, проходящей через три точки
аппроксимируется параболой, проходящей через три точки 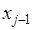 ,
,  ,
, 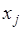 , то есть интерполяционным многочленом Лагранжа второй степени:
, то есть интерполяционным многочленом Лагранжа второй степени:
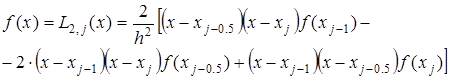 (2.12)
(2.12)
Проведя интегрирование, получим:
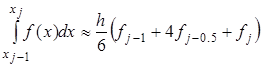 (2.13)
(2.13)
Это и есть формула Симпсона или формула парабол. На отрезке 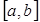 формула Симпсона примет вид:
формула Симпсона примет вид:
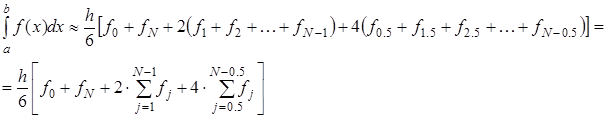 (2.14)
(2.14)
Если разбить отрезок интегрирования 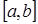 на четное количество 2N равных частей с шагом
на четное количество 2N равных частей с шагом 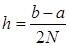 , то можно построить параболу на каждом сдвоенном частичном отрезке
, то можно построить параболу на каждом сдвоенном частичном отрезке 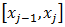 и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
 (2.15)
(2.15)
Графическое представление метода Симпсона показано на рис.2.4. На каждом из сдвоенных частичных отрезков заменяем дугу данной кривой параболой.

Рис.2.4. Метод Симпсона
Дата: 2019-04-23, просмотров: 447.