Рассмотрим уравнение
| f(x)=0 | (2.1) |
с отделенным корнем X 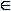 [a, b]. Для решения уравнения (2.1) методом простой итерации приведем его к равносильному виду:
[a, b]. Для решения уравнения (2.1) методом простой итерации приведем его к равносильному виду:
| x=φ(x) | (2.2) |
Это всегда можно сделать, причем многими способами. Например: x=g(x) · f(x) + x ≡ φ(x), где g(x) - произвольная непрерывная функция, не имеющая корней на отрезке [a,b].
Пусть x(0) - полученное каким-либо способом приближение к корню x (в простейшем случае x(0)=(a+b)/2). Метод простой итерации заключается в последовательном вычислении членов итерационной последовательности:
| x(k+1)=φ(x(k)), k=0, 1, 2, ... | (2.3) |
начиная с приближения x(0).
УТВЕРЖДЕНИЕ 2.1 Если последовательность {x(k)} метода простой итерации сходится и функция φ непрерывна, то предел последовательности является корнем уравнения x=φ(x)
ДОКАЗАТЕЛЬСТВО: Пусть
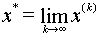
| (2.4) |
Перейдем к пределу в равенстве x(k+1)=φ(x(k)) Получим с одной сторонv по (2.4), что 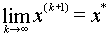 а с другой стороны в силу непрерывности функции φ и (2.4)
а с другой стороны в силу непрерывности функции φ и (2.4)
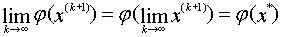
В результате получаем x*=φ(x*). Следовательно, x* - корень уравнения (2.2), т.е. X=x*
Чтобы пользоваться этим утверждением нужна сходимость последовательности {x(k)}. Достаточное условие сходимости дает:
ТЕОРЕМА 2.1 (о сходимости) Пусть уравнение x=φ(x) имеет единственный корень на отрезке [a,b] и выполнены условия:
1) φ (x) 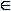 C1[a,b];
C1[a,b];
2) φ(x) 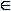 [a,b]
[a,b]  x
x 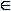 [a,b];
[a,b];
3) существует константа q > 0: | φ '(x) | ≤ q < 1  x
x 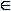 [a,b]. Tогда итерационная последовательность {x(k)}, заданная формулой x(k+1) = φ(x(k)), k=0, 1, ... сходится при любом начальном приближении x(0)
[a,b]. Tогда итерационная последовательность {x(k)}, заданная формулой x(k+1) = φ(x(k)), k=0, 1, ... сходится при любом начальном приближении x(0) 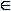 [a,b].
[a,b].
ДОКАЗАТЕЛЬСТВО Рассмотрим два соседних члена последовательности {x(k)}: x(k) = φ(x(k-1)) и x(k+1) = φ(x(k)) Tак как по условию 2) x(k) и x(k+1) лежат внутри отрезка [a,b], то используя теорему Лагранжа о средних значениях получаем:
x (k+1) - x (k) = φ (x (k)) - φ (x (k-1)) = φ '(c k )(x (k) - x (k-1))
где c k 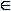 (x (k-1), x (k)).
(x (k-1), x (k)).
Отсюда получаем:
| | x (k+1) - x (k) | = | φ '(c k ) | · | x (k) - x (k-1) | ≤ q | x (k) - x (k-1)| ≤ ≤ q ( q | x (k-1) - x (k-2) | ) = q 2 | x (k-1) - x (k-2) | ≤ ... ≤ q k | x (1) - x (0) | | (2.5) |
Рассмотрим ряд
| S∞ = x (0) + ( x (1) - x (0) ) + ... + ( x (k+1) - x (k) ) + ... . | (2.6) |
Если мы докажем, что этот ряд сходится, то значит сходится и последовательность его частичных сумм
Sk = x (0) + ( x (1) - x (0) ) + ... + ( x (k) - x (k-1) ).
Но нетрудно вычислить, что
| Sk = x (k) | (2.7) |
Следовательно, мы тем самым докажем и сходимость итерационной последовательности {x(k)}.
Для доказательства сходимости pяда (2.6) сравним его почленно (без первого слагаемого x(0)) с рядом
| q 0 | x (1) - x (0) | + q 1 |x (1) - x (0)| + ... + |x (1) - x (0)| + ..., | (2.8) |
который сходится как бесконечно убывающая геометрическая прогрессия (так как по условию q < 1). В силу неравенства (2.5) абсолютные величины ряда (2.6) не превосходят соответствующих членов сходящегося ряда (2.8) (то есть ряд (2.8) мажорирует ряд (2.6). Следовательно ряд (2.6) также сходится. Tем самым сходится последовательность {x(0)}
Получим формулу, дающую способ оценки погрешности |X - x (k+1)| метода простой итерации.
Имеем X - x(k+1) = X - Sk+1 = S∞ - Sk+1 = (x(k+2) - (k+1) ) + (x(k+3) - x(k+2) ) + ... . Следовательно |X - x(k+1)| ≤ |x(k+2) - (k+1) | + |x(k+3) - x(k+2) | + ... ≤ qk+1 |x(1) - x(0) | + qk+2 |x(1) - x(0) | + ... = qk+1|x(1) - x(0) | / (1-q)
В результате получаем формулу
| |X - x(k+1)| ≤ qk+1|x(1) - x(0) | / (1-q) | (2.9) |
Взяв за x(0) значение x(k), за x(1) - значение x(k+1) (так как при выполнении условий теоремы такой выбор возможен) и учитывая, что при имеет место неравенство qk+1 ≤ q выводим:
|X - x(k+1)| ≤ qk+1|x(k+1) - x(k) | / (1-q) ≤ q|x(k+1) - x(k) | / (1-q)
Итак, окончательно получаем:
| |X - x(k+1)| ≤ q|x(k+1) - x(k) | / (1-q) | (2.10) |
Используем эту формулу для вывода критерия окончания итерационной последовательности. Пусть уравнение x=φ(x) решается методом простой итерации, причем ответ должен быть найден с точностью ε , то есть |X - x(k+1)| ≤ ε. С учетом (2.10) получаем, что точность ε будет достигнута, если выполнено неравенство
| |x(k+1)-x(k)| ≤ (1-q)/q | (2.11) |
Tаким образом для нахождения корней уравнения x=φ(x) методом простой итерации с точностью нужно продолжать итерации до тех пор, пока модуль разности между последними соседними приближениями остается больше числа ε(1-q)/q.
ЗАМЕЧАНИЕ 2.2 В качестве константы q обычно берут оценку сверху для величины 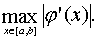
ПРИМЕР 2.1 Составим последовательность для решения уравнения f(x)=x·ex=0 по методу простой итерации.
Приведем уравнение к итерационному виду:
x = e - x ≡ φ(x).
Далее графически произведем отделение корня.
Несложный анализ графика показывает, что корень X 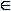 [e-1,1]. Tак как
[e-1,1]. Tак как 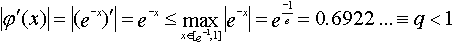 при x
при x 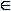 [e-1,1] и e-x
[e-1,1] и e-x 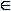 [e-1,1] ,
[e-1,1] ,  x
x 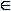 [e-1,1], то в соответствии с теоремой итерационная последовательность x(k+1) = e - x(k) , k=0, 1, 2, ... гарантированно сходится к корню уравнения. В качестве начального приближения к корню можно взятьx(0)=0.5(1+e-1).
[e-1,1], то в соответствии с теоремой итерационная последовательность x(k+1) = e - x(k) , k=0, 1, 2, ... гарантированно сходится к корню уравнения. В качестве начального приближения к корню можно взятьx(0)=0.5(1+e-1).
Метод прямоугольников
Дата: 2019-04-23, просмотров: 324.