Выше были рассмотрены три схожих метода интегрирования функций – метод прямоугольников, метод трапеций, метод Симпсона. Их объединяет общая идея: интегрируемая функция интерполируется на отрезке интегрирования по равноотстоящим узлам многочленом Лагранжа, для которого аналитически вычисляется значение интеграла. Семейство методов, основанных на таком подходе, называется методами Ньютона-Котеса.

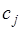В выражении коэффициенты правильнее называть весовыми коэффициентами. Величину 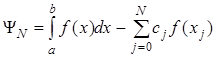, определяющую погрешность численного интегрирования, называют остатком.

Для семейства методов Ньютона-Котеса можно записать общее выражение:

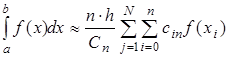(2.16)

где n – порядок метода Ньютона-Котеса, N – количество частичных отрезков, , , .

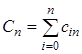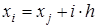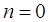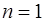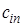Из выражения (2.16) легко можно получить формулу прямоугольников для , формулу трапеций для , и формулу Симпсона для . Коэффициенты могут быть заданы в табличной форме (таблица.2.1).

n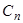
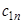
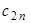
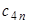
0	1	1
1	2	1	1
2	6	1	4	1
3	8	1	3	3	1
4	90	7	32	12	32	7
5	288	19	75	50	50	75	19

Таблица 2.1. Весовые коэффициенты метода Ньютона-Котеса

Метод Зейделя

Метод Зейделя (иногда называемый методом Гаусса-Зейделя) является модификацией метода простой итерации, заключающейся в том, что при вычислении очередного приближения x^(k+1) (см. формулы (1.13),(1.14)) его уже полученные компоненты x₁^(k+1), ...,x_{i - 1}^(k+1) сразу же используются для вычисления x_i^(k+1).

В координатной форме записи метод Зейделя имеет вид:

x₁^(k+1) = c₁₁x₁^(k) + c₁₂x₂^(k) + ... + c_1n-1x_n-1^(k) + c_1nx_n^(k) + d₁
x₂^(k+1) = c₂₁x₁^(k+1) + c₂₂x₂^(k) + ... + c_2n-1x_n-1^(k) + c_2nx_n^(k) + d₂
...
x_n^(k+1) = c_n1x₁^(k+1) + c_n2x₂^(k+1) + ... + c_nn-1x_n-1^(k+1) + c_nnx_n^(k) + d_n
где x⁽⁰⁾ - некоторое начальное приближение к решению.

Таким образом i-тая компонента (k+1)-го приближения вычисляется по формуле

Условие окончания итерационного процесса Зейделя при достижении точности ε в упрощенной форме имеет вид:

|| x ^(k+1) - x ^(k) || ≤ ε.

Существует более точное условие окончания итерационного процесса, которое более сложно и требует дополнительных вычислений (см., например, [1, стр.327]).

3. Метод хорд

Пусть f(a)f(b)<0. Сущность метода (его еще называют методом ложного положения) состоит в замене кривой y=f(x) хордами, проходящими через концы отрезков, в которых f(x) имеет противоположные знаки. Метод хорд требует, чтобы один конец отрезка, на котором ищется корень, был неподвижен. В качестве неподвижного конца х₀ выбирают тот конец отрезка, для которого знак f(x) совпадает со знаком второй производной 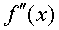. Расчетная формула имеет вид

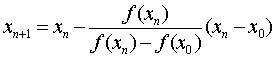
Метод хорд является двухточечным, его сходимость монотонная и односторонняя.

4. Метод Логранджа

Многочлен Лагранжа

При глобальной интерполяции на всем интервале 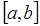строится единый многочлен. Одной из форм записи интерполяционного многочлена для глобальной интерполяции является многочлен Лагранжа:

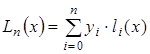(3.11)

где 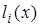– базисные многочлены степени n:

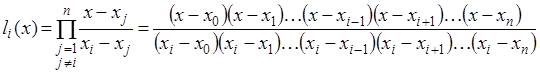(3.12)

То есть многочлен Лагранжа можно записать в виде:

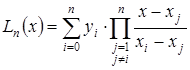(3.13)

Многочлен 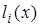удовлетворяет условию 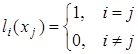. Это условие означает, что многочлен равен нулю при каждом 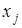кроме 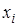, то есть – корни этого многочлена. Таким образом, степень многочлена равна n и при 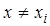обращаются в ноль все слагаемые суммы, кроме слагаемого с номером 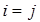, равного .

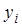Выражение (3.11) применимо как для равноотстоящих, так и для не равноотстоящих узлов. Погрешность интерполяции методом Лагранжа зависит от свойств функции , от расположения узлов интерполяции и точки x. Полином Лагранжа имеет малую погрешность при небольших значениях n (n<20). При больших n погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (то есть его погрешность не убывает с ростом n).

Многочлен Лагранжа в явном виде содержит значения функций в узлах интерполяции, поэтому он удобен, когда значения функций меняются, а узлы интерполяции неизменны. Число арифметических операции, необходимых для построения многочлена Лагранжа, пропорционально 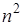и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что с изменением числа узлов приходится все вычисления проводить заново.

Кусочно-линейная и кусочно-квадратичная локальные интерполяции являются частными случаями интерполяции многочленом Лагранжа.

Многочлен Ньютона

Другая форма записи интерполяционного многочлена – интерполяционный многочлен Ньютона с разделенными разностями. Пусть функция задана с произвольным шагом, и точки таблицы значений пронумерованы в произвольном порядке.

Разделенные разности нулевого порядка совпадают со значениями функции в узлах. Разделенные разности первого порядка определяются через разделенные разности нулевого порядка:

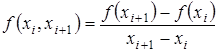(3.14)

Разделенные разности второго порядка определяются через разделенные разности первого порядка:

(3.15)

Разделенные разности k-го порядка определяются через разделенные разности порядка :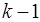

(3.16)

Используя понятие разделенной разности интерполяционный многочлен Ньютона можно записать в следующем виде:

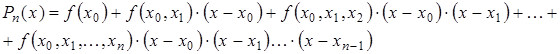(3.17)

За точностью расчета можно следить по убыванию членов суммы (3.17). Если функция достаточно гладкая, то справедливо приближенное равенство . Это приближенное равенство можно использовать для практической оценки погрешности интерполяции: .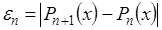

4. Метод Эйлера

Рассмотрим дифференциальное уравнение

(1)

с начальным условием

Подставив 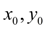в уравнение (1), получим значение производной в точке :

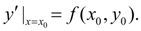
При малом 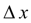имеет место:

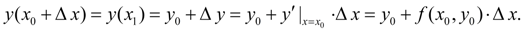
Обозначив 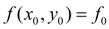, перепишем последнее равенство в виде:

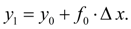(2)

Принимая теперь 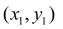за новую исходную точку, точно также получим:

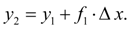
В общем случае будем иметь:

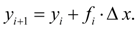(3)

Это и есть метод Эйлера. Величина 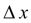называется шагом интегрирования. Пользуясь этим методом, мы получаем приближенные значения у , так как производная 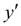на самом деле не остается постоянной на промежутке длиной 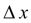. Поэтому мы получаем ошибку в определении значения функции у , тем большую, чем больше 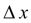. Метод Эйлера является простейшим методом численного интегрирования дифференциальных уравнений и систем. Его недостатки – малая точность и систематическое накопление ошибок.

Более точным является модифицированный метод Эйлера с пересчетом. Его суть в том, что сначала по формуле (3) находят так называемое «грубое приближение» (прогноз):

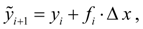
а затем пересчетом 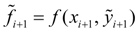получают тоже приближенное, но более точное значение (коррекция):

(4)

Фактически пересчет позволяет учесть, хоть и приблизительно, изменение производной 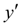на шаге интегрирования 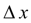, так как учитываются ее значения 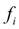в начале и 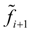в конце шага (рис. 1), а затем берется их среднее. Метод Эйлера с пересчетом (4) является по существу методом Рунге-Кутта 2-го порядка [2], что станет очевидным из дальнейшего.

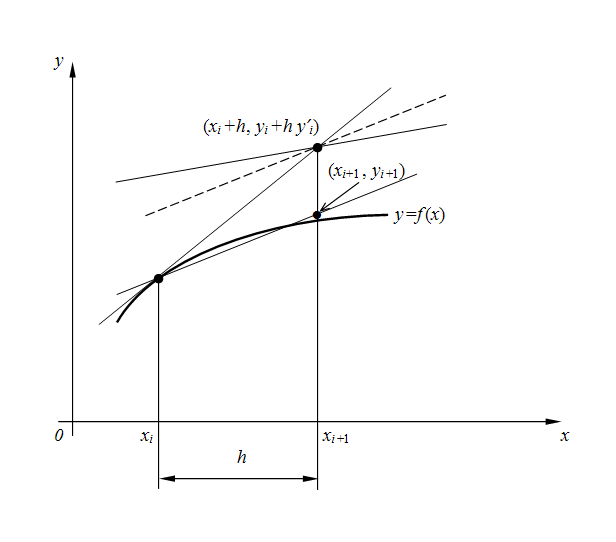
Рис. 1. Геометрическое представление метода Эйлера с пересчетом.