СИЛЛОГИЗМ - Логическое заключение, сделанное из двух посылок.

Простой категорический силлогизм — дедуктивное умозаключение, состоящее из трёх простых атрибутивных высказываний: двух посылок и одного заключения. Посылки силлогизма разделяются на бо́льшую (которая содержит предикат заключения) и меньшую (которая содержит субъект заключения). По положению среднего термина силлогизмы делятся на фигуры, а последние по логической форме посылок и заключения — на модусы.

Пример: Всякий человек смертен (бо́льшая посылка)

Сократ — человек (меньшая посылка)

Сократ смертен (заключение)

В силлогизм входит три термина:

S — меньший термин: субъект заключения (входит также в меньшую посылку);

Подлежащие S (субъект) — то, относительно чего мы высказываем (делится на два вида):

Определённое: Единичное, Частное, Множественное

Единичные [суждения] — в которых подлежащее является индивидуальным понятием. Прим: «Ньютон открыл закон тяготения»

Частное суждение — в котором подлежащим суждения является понятие, взятое в части своего объёма. Прим: «Некоторые S суть P»

Множественное суждение — это те, в которых несколько подлежащих классовых понятий. Прим: «насекомые, пауки, раки есть членистоногие»

Неопределённое. Прим: «светает», «больно» и т. п.

P — больший термин: предикат заключения (входит также в большую посылку);

Сказуемое P (предикат) — то, что мы высказываем (2 вида суждений):

Повествовательные — это суждение относительно событий, состояний, процессов или деятельности скоропроходящих. Прим: «Роза в саду цветет».

Описательные — когда одному или многим предметам приписывается какое-нибудь свойство. Субъектом всегда является определённая вещь. Прим: «Огонь горяч», «снег бел».

Отношение между подлежащим и сказуемым:

1. Суждения тождества — понятия субъекта и предиката имеют один и тот же объём. Прим: «всякий равносторонний треугольник есть равноугольный треугольник»

1. Суждения подчинения — понятия с менее широким объёмом подчиняется понятию с более широким объёмом. Прим: «Собака есть домашнее животное»
2. Суждения отношения — именно пространства, времени, отношения. Прим: «Дом находится на улице»

M — средний термин: входит в обе посылки, но не входит в заключение.

Правила простого категорического силлогизма:

· Средний термин должен быть распределён хотя бы в одной из посылок.

· Термин, не распределённый в посылке, не должен быть распределён в заключении.

· Число отрицательных посылок должно быть равно числу отрицательных заключений.

· В каждом силлогизме должно быть только три термин

Фигуры силлогизма – разновидности силлогизма, различаемые по положению среднего термина М в посылках.

Правила фигур:

1. Первая фигура силлогизма – это такое расположение его терминов, при котором первая посылка начинается со среднего термина, а вторая заканчивается средним термином.

ПРИМЕР: Все газы (М) – это химические элементы (Р).

Гелий (S) – это газ (М).

Гелий (S) – это химический элемент (Р).

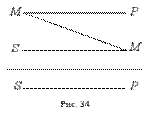
2. Вторая фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки заканчиваются средним термином.

ПРИМЕР:

Все рыбы (Р) дышат жабрами (М).

Все киты (S) не дышат жабрами (М).

Все киты (S) не рыбы (Р).

3. Третья фигура силлогизма – это такое расположение его терминов, при котором и первая, и вторая посылки начинаются со среднего термина. Например:

ПРИМЕР: Все тигры (М) – это млекопитающие (Р).

Все тигры (М) – это хищники (S).

Некоторые хищники (S) – это млекопитающие (Р).

Четвёртая фигура силлогизма – это такое расположение его терминов, при котором первая посылка заканчивается средним термином, а вторая начинается с него.

ПРИМЕР: Все квадраты (Р) – это прямоугольники (М).

Все прямоугольники (М) – это не треугольники (S).

Все треугольники (S) – это не квадраты (Р)

Условные умозаключения.

Чисто условным умозаключением называется такое опосред­ствованное умозаключение, в котором обе посылки являются условными суждениями. Условным называется суждение, име­ющее структуру: «Если а, то b».

Структура его такая: Если a, то b

Схема: Если b, то c a->b, b->c      Если a, то c a->c

Согласно определению логического следствия, сформулиро­ванному в рамках исчисления высказываний, если а -> с есть логи­ческое следствие из данных посылок, то, соединив посылки зна­ком конъюнкции и присоединив к ним посредством знака имп­ликации заключение, мы должны получить формулу, которая является законом логики. Формула будет такова:

ПРИМЕР: Если по проводнику пропустить электрический ток, то вокруг проводника образу­ется магнитное поле > Если вокруг проводника образуется магнитное поле, то железные опилки рас­полагаются в этом магнитном поле вдоль силовых линий. > Если по проводнику пропустить электрический ток, то железные опилки рас­полагаются в его магнитном поле вдоль силовых линий.

Формула: Формула является законом логики. В этом умозаключении суждение b истинно независимо от того, утверждается или от­рицается а.

Примером такого умозаключения является следующее рас­суждение: Если будет хорошая погода, уберем урожай > Если не будет хорошей погоды, уберем урожай. > Уберем урожай.

Приведем пример из художественной литературы. Один из героев Агаты Кристи, оказавшийся на острове, рассуждает: «Генерал Макартур пребывал в мрачной задумчивости. Черт побе­ри, до чего все странно! Совсем не то, на что он рассчитывал... Будь хоть малейшая возможность, он бы под любым предлогом уехал... Ни минуты здесь не остался бы... Но моторка ушла. Так что хочешь не хочешь, а придется остаться».

Условно-категорическое умозаключение — это такое дедук­тивное умозаключение, в котором одна из посылок — условное суждение, а другая — простое категорическое суждение.

Оно имеет два правильных модуса, дающих заключение, с не­обходимостью следующее из посылок.

I. Утверждающий модус .Формула (1):— является законом логики. Можно строить достоверные умозаключения от утвержде­ния основания к утверждению следствия. Приведем два примера. Если ты хочешь наслаждаться искусством, то ты должен быть художественно образованным человеком. + Ты хочешь наслаждаться искусством = Ты должен быть художественно образованным человеком. ИЛИ Если этот металл натрий, то он легче воды.+Данный металл — натрий.=Данный металл легче воды.

II. Отрицающий модус . Формула (2):— также является законом логики. Можно строить достоверные умозаключения от отрицания следствия к отрицанию основания.Приведем два примера. Если река выходит из берегов, то вода заливает прилегающие территории. + Вода реки не залила прилегающие территории. = Река не вышла из берегов.

Формула (3): — не является законом логики.Нельзя получить достоверное заключение, идя от утвержде­ния следствия к утверждению основания. Например, в умозак­лючении: Если бухта замерзла, то суда не могут входить в бухту. +Суда не могут входить в бухту = Вероятно, бухта замерзла.

Формула (4):— не является законом логики. Нельзя получить достоверное заключение, идя от отрицания основания к отрицанию следствия. Например: Если человек имеет повышенную температуру, то он болен + Этот человек не имеет повышенной температуры = Вероятно, этот человек не болен.