Число тепловых нейтронов, поглощаемых в 1 см³ за 1 с, равно Σ_аФ, где Σ_а - макроскопическое сечение поглощения; Ф-плотность потока тепловых нейтронов. Следовательно, скорость генерации нейтронов (как мгновенных, так и запаздывающих) выражается величиной 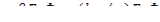  нейтронов в 1 см³ за 1 с, где θ - коэффициент использования тепловых нейтронов; η - число нейтронов, генерируемых при одном поглощении теплового нейтрона в топли­ве; μ - коэффициент размножения на быстрых нейтронах; φ — вероятность из­бежать резонансного захвата. Поскольку  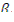—доля запаздывающих нейтронов i-й группы в общем числе нейтронов, испускаемых в акте деления, скорость об­разования предшественников, соответствующих указанной группе, равна 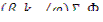в 1 см³ за 1 с. Если обозначить через с _i - концентрацию (в ядрах на 1 см³ ) предшественников запаздывающих нейтронов i-й группы, то скорость их радиоактивного распада будет равна λ_i с _i, ядер в 1 см³ за 1 с, где λ_i , с^-1 — соот­ветствующая постоянная распада. Таким образом, уравнение, описывающее Изменение со временем концентрации предшественников i -й группы запазды­вающих нейтронов, имеет вид

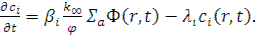                                                                   (12.13)                          

Уравнение диффузии тепловых нейтронов для случая, когда реактор нахо­дится в нестационарном состоянии, может быть записано в следующем виде:

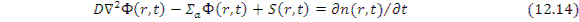
где D - коэффициент диффузии нейтронов; S - плотность источников нейтро­нов; n - плотность тепловых нейтронов. Первый член в левой части характери­зует диффузию нейтронов, второй - поглощение и третий — генерацию нейтро­нов. Правая часть уравнения представляет собой изменение плотности нейтро­нов во времени.

Поскольку учитывается генерация как мгновенных, так и запаздывающих нейтронов, в уравнении (12.14) плотность источников можно представить в ви­де суммы

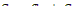
где 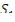 - плотность источников мгновенных нейтронов;  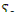— плотность источни­ков запаздывающих нейтронов.

Согласно теории возраста, член, учитывающий источники тепловых ней­тронов, обусловленные процессом деления, определяется произведением φq ( τ_т), где φ — вероятность избежать резонансного захвата; q — плотность за­медления нейтронов; τ_т —возраст тепловых нейтронов. Поскольку (1-β)-доля нейтронов, испускаемых мгновенно в акте деления, то плотность источников мгновенных нейтронов определяется выражением

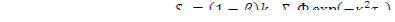                                       (12.15)     

Здесь 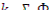 — число тепловых нейтронов в единице объема и в единицу време­ни, возникающих в результате процесса деления в бесконечной системе, т.е. в

2 отсутствие утечки. Множитель  представляет собой вероятность того,

что нейтрон избежит утечки в процессе замедления, где  - материальный па­раметр.

Скорость генерации запаздывающих нейтронов i-й группы равна скорости распада соответствующего предшественника, т. е. λ_i с _i, поэтому полная ско­рость генерации всех запаздывающих нейтронов в единице объема и в единицу времени равна 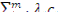, где суммирование распространено по всем группам запаздывающих нейтронов. Умножая эту величину на  (вероятность из­бежать утечки в процессе замедления) и на φ (вероятность избежать резонанс­ного захвата), получаем для члена, учитывающего источники запаздывающих нейтронов, выражение

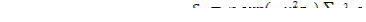                                                    (12.16)

С учетом выражений (12.15) и (12.16), а также соотношения Ф = nv уравне­ние (12.14) запишется в следующем виде:

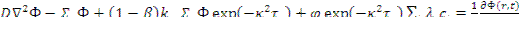       (12.17)

Разделив обе части уравнения на 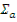, получим

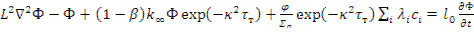          (12.18)                         

где 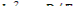- квадрат длины диффузии тепловых нейтронов;

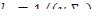 - среднее время жизни теплового нейтрона в бесконечной среде.

Допустим, что в момент t =0 реактор выходит из стационарного режима вследствие малого скачкообразного изменения коэффициента размножения, причем в течение всего последующего времени величина 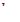 остается неизмен­ной. Можно показать, что в этом случае уравнение (12.18) допускает разделе­ние переменных. Будем считать, что реактор достаточно близок к критическому состоянию, так что нейтронный поток с хорошей степенью точности может быть описан основным решением волнового уравнения. Положим:

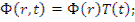                                                                                                        (12.19)

                                                 (12.20)

где 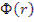 и 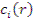 зависят только от координаты, a  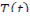и 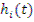                                                 — только от времени. Производя подстановку (12.19) и (12.20) в уравнение (12.13) и разделив все члены на 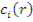, получим

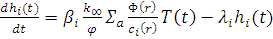                                                                      (12.21)                      

Из физических соображений величина 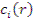 пропорциональна 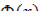, в урав­нении (12.21) отнношение  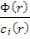не зависит от координат. В этом случае все члены уравнения являются функциями только времени.

Аналогично сделаем подстановку (12.19) и (12.20) в уравнение (12.18) и разделим все его члены на 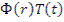. После этого будем иметь

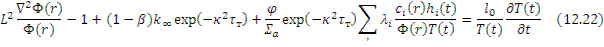
Поскольку 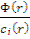 не зависит от координат, то переменные в уравнении раз­деляются.

Ввиду того, что переменные разделяются, возможно написать

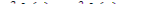
Поскольку оператор Лапласа не действует на функцию T ( t ), зависящую только от времени, то, умножая на нее, получим общий вид волнового уравнения

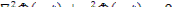
в котором величина 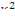 является наименьшим собственным значением и опре­деляется из граничного условия, состоящего в том, что поток тепловых нейтро­нов должен обращаться в нуль на экстраполированной границе. Таким образом, оказывается возможным заменить в уравнении (12.18) выражение  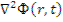на .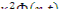

Задача сводится теперь к тому, чтобы решить уравнения (12.13) и (12.18), учитывая (12.24). При этом уравнение (12.18) перепишем в виде

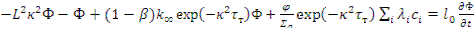         (12.25)

Уравнения (12.13) и (12.25) часто записывают с учетом плотности нейтро­нов n = Ф/ν:

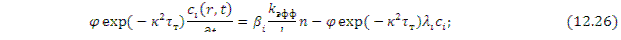
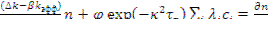                                                                       (12.27)

где 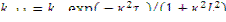 ; 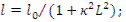по определению,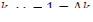

Обозначим , т.е. концентрация предшественников запаздывающих нейтронов с учетом того, что запаздывающие нейтроны достигли тепловой области, тогда как с_i относилось к предшествующему поколению. Так как концентрация ядер-предшественников запаздывающих нейтронов сама по себе несущественна, то 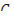 обычно тоже называется концентрацией предшест­венников, излучающих запаздывающие нейтроны [4]. С учетом этого уравне­ния (12.26) и (12.27) можно записать в виде:

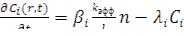                                                                                           (12.28)

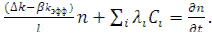                                                                              (12.29)