Предположим в первом приближении, что все нейтроны, освобождаемые в процессе деления, появляются в течение весьма короткого промежутка времени (порядка 10^-15 с); иначе говоря, полагаем здесь, что при делении возникают только мгновенные нейтроны.

Уравнение диффузии тепловых нейтронов (10.2) для случая, когда реактор на­ходится в нестационарном состоянии, может быть записано в следующем виде:

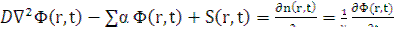 ,              (12.1)

где D - коэффициент диффузии нейтронов, см; Σ_α - макроскопическое сечение поглощения, см ^-1; Ф - плотность потока тепловых нейтронов, нейтрон/(см² с); S — плотность источников нейтронов, нейтрон/(см³ с); n —плотность тепловых нейтронов, нейтрон/см³ ; Ф = п ν; ν - скорость теплового нейтрона, см/с. Первый член в левой части характеризует диффузию нейтронов, второй - поглощение и третий - генерацию нейтронов. Правая часть уравнения представляет собой из­менение плотности нейтронов во времени.

Согласно теории возраста, член, учитывающий источники тепловых ней­тронов, обусловленные процессом деления, выражается произведением φq(τ_т) где φ - вероятность избежать резонансного захвата; q - плотность замедления нейтронов, нейтрон/(см³ с); τ_т - возраст тепловых нейтронов, см² , и дается фор­мулой (см. гл. 10):

S = k_∞Σ_αΦexp(-k² τ_т).                                                 (12.2)

 Здесь k_∞Σ_αΦ — число тепловых нейтронов в единице объема и в единицу време­ни, возникающих в результате процесса деления в бесконечной системе, т.е. в отсутствие утечки. Множитель exp(-k² τ_т) представляет собой вероятность того,что нейтрон избежит утечки в процессе замедления, где k² — материальный па­раметр, см^-2 . Подставляя формулу (12.2) в равенство (12.1) и предполагая, что внешние источники нейтронов отсутствуют, получаем

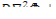Σ_αΦ(k_∞exp(-k² τ_т)-1) =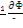

Разделив последнее уравнение на ∑_α и воспользовавшись соотношением D / Σ _α = L ² ,

где L - длина диффузии теплового нейтрона, получим

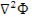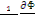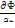L² + (k_∞exp(-k² τ_т)-1)Φ = = l ₀  ,                          (12.3)

где l ₀=1/(ν∑_α) = λ_α/ν - среднее время жизни теплового нейтрона в бесконечной среде [2] (λ_а — средняя длина свободного пробега нейтронов до поглощения). Данное уравнение решается методом разделения переменных. Положим

Φ≡Φ(r , t)=Φ(r)T(t) ,                                                   (12.4)

где r — вектор произвольной точки внутри реактора, a t — время. Функция Ф(r) зависит только от пространственных координат, T(t)  зависит только от времени. Подставив (12.4) в (12.3) и разделив обе части на (12.4), получим

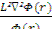 + k_∞exp(-k² τ_т)-1 =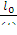 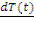 ,                                (12.5)

Предположим, что в момент t =0 реактор выведен из стационарного состояния в результате малого скачкообразного изменения коэффициента размножения k _∞ а затем величина k _∞ остается неизменной. При этом допущении левая часть уравнения (12.5) не зависит от времени, а правая часть не зависит от простран­ственных координат. Таким образом, действительно переменные разделяются.

Если система не далека от критического состояния, то пространственное распределение плотности потока нейтронов с достаточной степенью точности описывается волновым уравнением

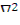Φ(r)+κ²Φ(r)=0 ,

где κ -геометрический параметр (см. гл. 10). Это дает возможность освободиться в уравнении (12.5) от отношения 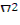Φ(r)/Φ(r),  т.е. написать

- (1+L²κ²)+ k_∞exp(-k² τ_т) =  .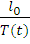

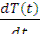Разделив обе части равенства на (1+L²κ²), получаем

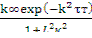 -1= 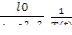 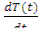,                                     (12.6)

Первый член левой части уравнения (12.6) представляет собой эффективный коэффициент размножения k_эфф [см.(10.8)], а первый множитель правой части равен l - среднему времени жизни теплового нейтрона в ограниченной среде с учетом утечки в тепловой области [2]. Таким образом, уравнение (12.6) сводит­ся к следующему соотношению:

 k_эфф-1 = 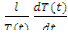 ,                                                          (12.7)

Превышение величины k_эфф  над единицей называется коэффициентом избы­точного размножения (мультипликации [2]) и обозначается через Δk. Таким образом,

Δk= k_эфф-1,                                                   (12.8)

Для критической системы k_эфф=1; следовательно, Δk представляет собой меру удаления реактора от критического состояния. Величина Δk положительна для реактора в надкритическом состоянии и отрицательна для реактора в подкритическом состоянии. Подставляя (12.8) в (12.7), получаем

Δk =  .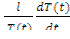

Интегрирование последнего выражения дает

T ( t )= A_exp(Δkt / l ),

или, принимая во внимание (12.4),

Ф(r , t)=AФ(r)exp(Δkt / l).                                    (12.9)

При t=0 Ф(r,t)=AФ(r). Таким образом, если обозначить Ф(г,0) через Ф₀, то формула (12.9) принимает вид

 Ф(r , t) = Ф₀(Δkt / l).                                  (12.10)

где Ф₀ - плотность стационарного потока тепловых нейтронов в точке r при t=0, т.е. в момент, когда эффективный коэффициент размножения реактора скачкообразно изменяется на величину Δk.

Период реактора

Время, в течение которого величина плотности нейтронного потока (или нейтронной плотности) изменяется в е раз, называется периодом реактора и обозначается через Т. Величину Т можно определить математически, если по­ложить:

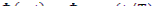                                                                                                    (12.11)

Сравнение этого выражения с формулой (12.10) показывает, что в рассматри­ваемом случае (т.е. предполагая, что при делении возникают только мгновен­ные нейтроны)

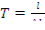                                                                                                                               (12.12)

Согласно приведенному ранее анализу, если реактор находится в нестацио­нарном состоянии ( 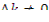), плотность потока тепловых нейтронов возрастает (или убывает) экспоненциально, причем показатель экспоненты определяется отношением среднего времени жизни теплового нейтрона к коэффициенту из­быточного размножения. Этот результат не является неожиданным, он может быть также получен из общих соображений, приведенных в гл. 5. Действитель­но, если пренебречь временем замедления, то легко видеть, что среднее время жизни теплового нейтрона по существу есть время жизни одного поколения нейтронов, а следовательно, полученная в гл. 5 зависимость для плотности ней­тронов от времени эквивалентна формуле (12.10). Период реактора оказывает­ся, таким образом, равным времени жизни одного поколения нейтронов, делен­ному на фактор избыточного размножения. Следует отметить, что полученный результат является совершенно общим, он справедлив как для мгновенных, так и для запаздывающих нейтронов. Однако следует подчеркнуть, что, среднее время жизни теплового нейтрона можно отождествлять с временем жизни од­ного поколения нейтронов только в том случае, когда все рождающиеся в про­цессе деления нейтроны являются мгновенными.

Как указывалось ранее, если реактор находится в надкритическом состоя­нии, k_эфф >1 и 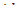 положительно. Отсюда следует, что и период реактора есть величина положительная. Это означает, что в надкритическом состоянии плот­ность потока нейтронов в реакторе возрастает с течением времени по экспонен­те в соответствии с формулой (12.10). Наоборот, в реакторе, находящемся в подкритическом состоянии, период, так же, как и 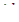, отрицателен и плотность потока нейтронов экспоненциально убывает.

Если эффективный коэффициент размножения скачкообразно увеличится на 0,01, т.е. 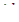 =0,01, то период большого реактора на тепловых нейтронах l≈0,001 с, согласно формуле (12.12), равен (0,001/0,01) с, т.е. 0,1 с. Следова­тельно, в течение каждой десятой доли секунды плотность нейтронного потока будет увеличиваться в е раз.