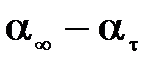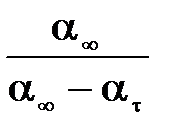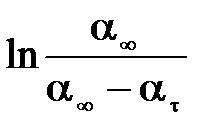Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

При изучении кинетики набухания полимера

Время с начала опыта, мин	Уровень жидкости в градуированной трубке,		Суммарное количество поглощенного растворителя
	мм	см	Vж, мл	mж, г (11)	a,% (1¢)
2					at1
4					at2
6					at3
8
10
15
20
30
40
50
60					a¥

 

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

 

1. Что такое набухание? Ограниченное и неораниченное набухание.

2. Что такое степень набухания?

3. Скорость и константа скорости набухания.

4. Графическое определение константы скорости набухания.

5. Интегральная и дифференциальная теплоты набухания.

6. Давление набухания.

7. Стадии процесса набухания.

 

ЛАБОРАТОРНАЯ РАБОТА №7

ДИСПЕРСИОННЫЙ АНАЛИЗ НИЗКОДИСПЕРСНЫХ ПОРОШКОВ МЕТОДОМ СЕДИМЕНТАЦИИ

 

Цель работы

 

Произвести дисперсионный анализ суспензии методом седиментации.

 

Задачи работы

 

1. Получить кривую седиментации для низкодисперсного порошка.

2. Построить интегральную и дифференциальную кривые распределения частиц по радиусам.

 

Приборы и материалы

 

· Стеклянные седиментационные весы Фигуровского.

· Стакан для суспензии.

· Мешалка.

· Секундомер.

· Термометр.

· Суспензия СаСО₃ в воде концентрации 10 мас. %.

· Микроскоп.

 

Теоретическое пояснение

1. Седиментационно-диффузионное равновесие

Частицы дисперсной фазы в гравитационном поле оседают, если их плотность больше плотности дисперсионной среды, или всплывают, если их плотность меньше плотности дисперсионной среды. Следствием процесса седиментации является возникновение градиента концентрации частиц по высоте сосуда, приводящего к диффузии, направленной в сторону меньшей концентрации.

Сравнение седиментационного (i_сед) и диффузного (i_диф) потоков поз­воляет установить, какой из процессов преобладает в данной дисперсной системе. Для нахождения закона распределения частиц по высоте исходят из равенства потоков диффузии и седиментации (i_сед=i_диф), т.е. из условия седи­ментационно-диффузионного равновесия. Поток седиментации рассчиты­вают по уравнению:

i_сед=u_седn,                                                (1)

где u_сед – линейная скорость седиментации; n – число частиц в единице объема (частичная концентрация).

Условием равномерного движения частиц является равенство силы тяжести и силы трения; последняя для сферической частицы радиуса r определяется по уравнению Стокса:

F=6phru_сед                                                                               (2)

Скорость седиментации с учетом поправки на потерю в массе по зако­ну Архимеда выразится уравнением:

u_сед=(mg/6phr)·(r-r₀/r)                          (3)

где m – масса частицы; g – ускорение свободного падения;

r и r₀ – плотность дисперсной фазы и дисперсионной среды.

Диффузионный поток рассчитывают по уравнению Фика:

i_диф= -D · (dn/dH)= -(kT/6phr) · (dn/dH) (4)

где (dn/dH) - градиент концентрации по высоте H; D-коэффициент диффузии.

Приравняв правые части уравнений (3) и (4), получают выражение седиментационно-диффузионного равновесия, называемое уравнением Лап­ласа-Перрена:

ln(n₀/n)=(mgH/kT) · (r-r₀/r)                  (5)

где n и n₀ – число частиц на исходном уровне и на высоте Н, соответственно.

Уравнение (5) является частным случаем универсального закона рас­пределения Больцмана:

n=n₀e^-U/kT                                                                                   (6)

где U-потенциальная энергия.

Для гравитационного поля с учетом поправки по закону Архимеда: U=mgH · (r-r₀/r)                                    (7)

Уравнение (5) было получено раньше независимо от закона Больцмана.

Определение размеров частиц может быть проведено двумя методами: по измерению скорости седиментации и на основании исследования распре­деления частиц по высоте.

Первый метод широко используется для грубодисперсных систем с размерами частиц более 10^-6 м. На этом методе основан седиментационный анализ грубодисперсных систем.

Второй метод определения размеров частиц – по седиментационно-диффузионному равновесию – непригоден для грубодисперсных систем (там практически отсутствует поступательное броуновское движение). Для коллоидных систем (размеры частиц 10^-7-10^-9 м) этот метод в гравита­ционном поле практически не используется, так как здесь существенно преобладает тепловое движение частиц над седиментацией.

Расчет показывает, что частицы размером 10^-7-10^-9 м удерживаются тепловым движением во взвешенном состоянии. Их концентрация во всем объеме остается практически постоянной – такие системы седиментационно устойчивы.

Метод определения размеров частиц по седиментационно-диффузионному равновесию успешно используется с применением центробежного поля, при этом регулирование скорости вращения центрифуги позволяет применять этот метод в достаточно большом интервале размеров. Используя ультра­центрифугу, можно определять также молекулярную массу полимеров.

2. Седиментация в гравитационном поле и основы седиментационного анализа

Так как частицы дисперсной фазы в грубодисперсионных системах сравнительно велики и не совершают поступательного броуновского движе­ния (оно возможно лишь для частиц размером меньше микрона), они сравни­тельно быстро оседают. Чем крупнее частицы дисперсной фазы, тем быстрее они оседают. Поэтому можно произвести разделение частиц полидисперсной суспензии на фракции по размерам - фракционирование суспензии, а также провести седиментационный анализ полидисперсной системы, т.е. уста­новить ее фракционный состав.

Для определения размеров частиц суспензии преобразуют уравнение (3) на основании следующих соображений: при равномерном движении час­тицы скорость седиментации:

u_сед=H/t                                                  (8)

где H – высота оседания; t - время оседания.

Поскольку масса сферической частицы радиуса r: m=vr=4/3(pr³r), где v- объем сферической частицы, то подставив приведенные выше выражения для u_сед и m в уравнение (3), получим:

u_сед=H/t=4/3(pr³rg/6phr)(r-r₀/r)=2/9(r²g(r-r₀)/h) (9)

откуда:

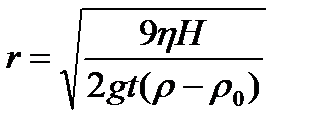                                       (10)

В уравнении (10) выражение:

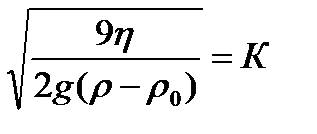                                     (11)

есть величина постоянная для данной системы и условий опыта (константа седиментации). Следовательно,

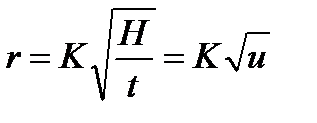                                      (12)

Уравнения (2) и (12) справедливы лишь для твердых сферических частиц, движущихся равномерно с небольшой скоростью в среде, которую можно считать безграничной по отношению к падающей частице. Расстояние между падающими частицами должно быть велико, чтобы не было взаимо­действия между ними и падение одних частиц не отражалось на скорости других; поэтому анализ ведут обычно в суспензиях с концентрацией не выше 1 мас. %. Суспензия должна быть агрегативно устойчивой, т.е. частицы не должны коагулировать за время седиментации.

Реальные суспензии очень часто содержат частицы, сильно отличаю­щиеся по форме от шарообразных. При исследовании таких суспензий с по­мощью седиментационного анализа радиус частиц, подсчитанный по урав­нению (12), представляет собой радиус воображаемых шарообразных частиц из того же материала, оседающих с той же скоростью, что и частицы изучае­мой суспензии. Вычисленный таким образом радиус называется эквивалент­ным.

Существует несколько принципов седиментационного анализа. К первой группе относятся методы, в которых анализ проводится с разделением дисперсной фазы на отдельные фракции; это может происходить в спокойной жидкости, а также в текущей струе жидкости. Во вторую группу входят методы, в которых не производится непосредственное разделение дисперсной системы на фракции: к ним относится гравиметрический (весовой) метод анализа. В последнем случае по результатам непрерывного определения массы седиментационного остатка строят седиментационную кривую – зависимость массы седиментационного осадка m от времени оседания t (рис. 1в). В реальных полидисперсных системах кривые оседания имеют плавный ход. Затем экспериментальную седиментационную кривую обрабатывают либо графическим способом (путем построения касательных в точках кривой, соответствующих разным значениям t) и получают данные для построения интегральной и дифференциальной кривых распределения, либо пользуются аналитическим методом расчета кривых распределения.

Седиментационный анализ проводят на весах Фигуровского или с помощью торсионных весов. В литературе имеется сравнительный анализ некоторых конструкций седиментометров, выпускаемых серийно заграничными фирмами. Их действие основано либо на измерении массы седиментационного осадка, либо на определении концентрации суспензии по погло­щению излучения в оптическом или рентгеновском диапазоне длин волн, а также потоков частиц (оптические седиментометры).

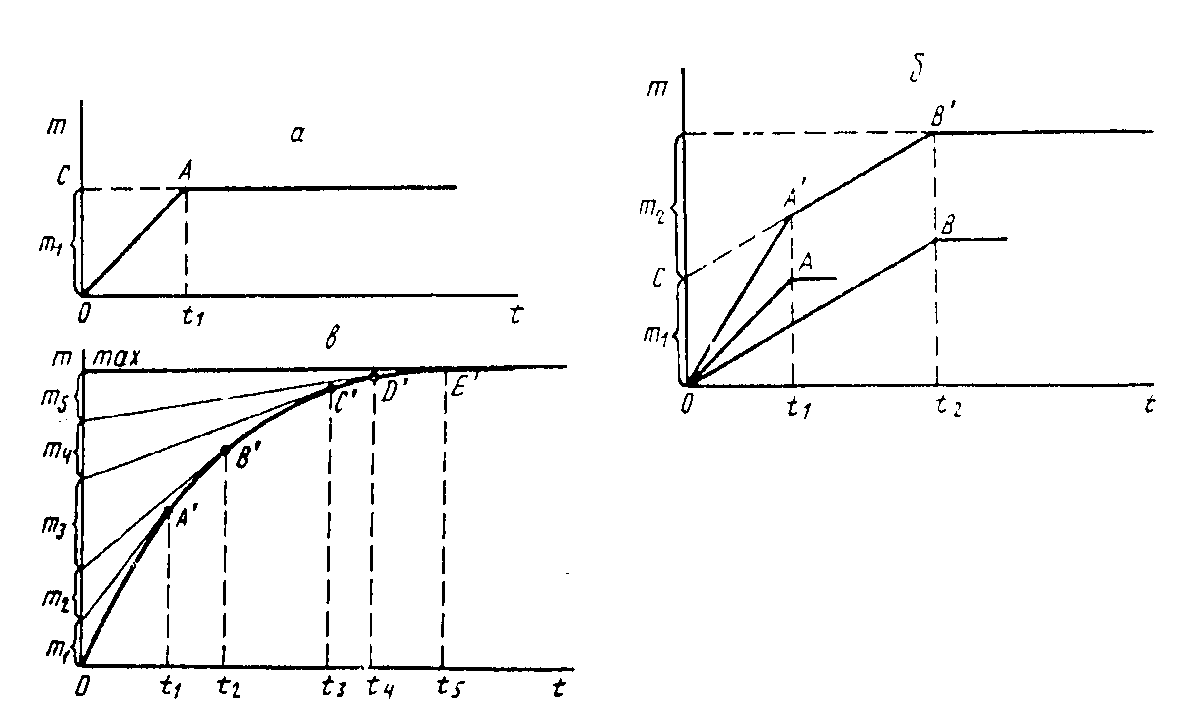
Рис.1. Зависимость массы осадка суспензий от времени для монодисперсной (а), бидисперсной (б), полидисперсной (в) систем.

На рис. 1 показана зависимость массы осадка m от времени оседания t для различных систем. Для монодисперсной системы (рис. 1а) масса осадка прямо пропорциональна времени оседания. В точке А оседание всех частиц закончилось, далее масса осадка не изменяется. Время t₁ соответствующее точке А, есть время прохождения частицами пути Н от поверхности суспен­зии до чашечки (рис. 2). По величинам Н и t₁ рассчитывают u по равенству (8), а затем r₁ (12).

Пусть дисперсная система состоит из двух монодисперсных систем. Процесс осаждения каждой фракции представлен прямыми ОА и ОВ (рис. 1б). Суммарная кривая осаждения получается графическим сложением ординат прямых ОА и ОВ. Суммарная кривая имеет изломы в точках А¢ и Б′. Абсцисса точки А соответствует времени оседания более крупных частиц (t₁), а время t₂ соответствует оседанию более мелких частиц. Отрезок ОС, отсекаемый на оси ординат продолжением прямой А¢В¢, соответствует массе более крупной фракции m₁; отрезок m₂ соответствует массе мелкой фракции.

График седиментации полидисперсной системы (рис. 1в) представляет собой плавную кривую с бесконечно большим числом изломов. Для количественного анализа полидисперсной системы ось абсцисс графика седиментации разбивают на участки, соответствующие времени осаждения различных фракций. Чем больше число фракций будет выбрано для исследования, тем точнее будет полученная кривая распределения полидисперсной системы. Из точек кривой A¢, B¢, C¢, D¢, E¢, соответствующих моментам полного осаждения фракций, проводят касательные к кривой до их пересечения с осью ординат (рис. 1в). Полученные отрезки ординат показывают массы выбранных фракций. Например, фракция, радиус частиц которой может быть рассчитан по времени ее полного осаждения t₁, имеет массу m₁ и т. д. Определив массы отдельных фракций, а также массу осадка на чашке после полного осаждения суспензии m_макс, рассчитывают процентное содержание отдельных фракций:

Q_i= (m_i/m_макс)·100                                  (13)

где Q_i - содержание фракции, % ; m_i - масса фракции, мг; m_макс- общая масса осадка на чашке после полного осаждения частиц суспензии, мг.

Величину Q₁ удобнее рассчитывать, если вместо значений масс m_i и m_макс в формулу (13) подставить пропорциональные им длины отрезков ординаты в миллиметрах.

При построении кривой седиментации полидисперсной системы реко­мендуется масштаб: ось ординат - в 1см 10 мг; ось абсцисс - в 1см 60 с.

ВЫПОЛНЕНИЕ РАБОТЫ

Весовая модификация седиментационного анализа заключается в определении скорости накопления осадка на чашке весов. Для этой цели были предложены седиментационные весы самых разнообразных конструкций. Наиболее распространенными седиментационными весами является прибор Н.А. Фигуровского, предложенный им в 1936 г.

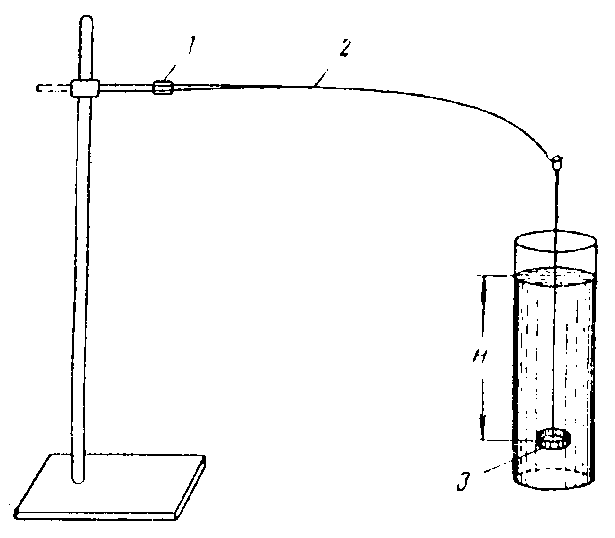
Рис. 2. Седиментометр Фигуров­ского: 1) держатель штатива, 2) шпиц, 3) чашечка, 4) цилиндр.

Этот прибор (рис. 2) представляет собою закрепленный в горизонтальном положении в держателе штатива 1 гибкий стеклянный или кварцевый шпиц (коромысло) 2. Коромысло имеет длину от 20 до 50 см, в зависимости от условий опыта. На тонком конце шпица сделан крючок, к которому подвешивается на длинной стеклянной нити, толщиной около 0,2 -0,5 мм, легкая плоская тонкостенная стеклянная чашечка 3. Расстояние от дна чашечки до поверхности суспензии (высота Н) должно составлять ~ 15-20 см, от чашечки до дна цилиндра ~ 2–3 см (при больших расстояниях могут быть не учтены самые крупные частицы). Опыт производится следующим образом.

Собирается прибор и проверяется прочность закрепления коромысла и устойчивость всех частей прибора. Чашечку подвешивают в центре цилиндра, наполненного исследуемой суспензией. Микроскоп наводят на конец нагруженного коромысла так, чтобы метка, по которой производится отсчет деформации, находилась в нижней части от счетной шкалы микроскопа. Так как микроскоп дает обратное изображение, то при увеличении нагрузки коромысла метка будет передвигаться вверх.

Прежде чем приступить к седиментационному анализу, проверяют, происходит ли деформация коромысла по закону Гука. Для этого на чашечку помещают разновес и отмечают его деформацию при нагрузке от 20 до 200 мг (пользуясь отсчетным микроско­пом). Результаты опыта записывают в таблицу 1.

Таблица 1.

Данные для построения зависимости Е=f(m)

m, мг	Е

Полученные данные наносят на график, причем по оси ординат откла­дывают деления микроскопа Е, а по оси абсцисс – нагрузку m, мг (рис. 3).

E

m, мг

•

•

•

•

α

ctgα=k

Рис. 3. Зависимость деформации коромысла от нагрузки Е=f(m).

В случае применимости закона Гука зависимость деформации от наг­рузки m должна быть прямолинейной. По ctgα находят коэффициент k для пересчета значений Е в m: m = k · E.

Суспензию хорошо размешивают мешалкой в течение 3-5 мин. При этом рекомендуется энергичное размешивание мешалкой, приводящее к появлению в суспензии мельчайших пузырьков воздуха. После окончания размешивания в суспензию очень быстро опускают чашечку, подвешенную на крючок коромысла, и производят первый отсчет по микроскопу. Следует стремиться к тому, чтобы с момента погружения чашечки в суспензию до первого отсчета прошло не более 15-20 с. Дальнейшие отсчеты можно произ­водить через промежутки времени, в которые конец коромысла передвига­ется на одно деление. Результаты опыта записывают в таблицу 2. Анализ считают законченным, когда два последних измерения с интервалом времени между ними не менее 5 мин совпадают.  

Таблица 2.