Все электрокинетические явления связаны с относительным перемещением дисперсной фазы и дисперсионной среды, осуществляемой по границе скольжения. Их интенсивность определяется значением x-потенциала. Поэтому данную величину используют для оценки электрокинетических явлений.
Двойной электрический слой можно рассматривать в качестве своеобразного конденсатора (рис. 6).
| h/2 |
| f1 |
| f2 |
| 2 |
| 1 |
| 3 |
| Б |
| Б |
Рис. 6. Схема возникновения электрокинетических явлений: 1 – потенциалобразующий слой ионов; 2, 3 – противоионы в адсорбционном (2) и диффузном (3) слоях; нижняя стрелка показывает направление движение жидкости.
Относительность движения дисперсной фазы и дисперсионной среды определяется силами f1 и f2. Сила f1 возникает в результате взаимодействия избытка зарядов потенциалобразующего слоя по отношению к адсорбционному слою; она характеризует заряд диффузного слоя и направлена параллельно границе скольжения (линия ББ), противодействуя силе трения. Сила f1 определяется по формуле (1)
f1 =ЕqВ, (1)
где Е – напряженность или градиент внешнего поля; qВ – плотность заряда поверхности.
Сила f2 определяет трение жидкости при ее перемещении:
f2=h(v/h), (2)
где h – коэффициент трения (см. приложение, таблица 4); v – скорость движения жидкости; h – расстояние между поверхностями.
При установившемся движении эти силы равны f1=f2, т.е.
ЕqВ=h(v/h), или v =(qВh/h)Е. (3)
Формула (3) определяет скорость взаимного перемещения дисперсной фазы и дисперсионной среды. Удельный заряд qВ можно связать с x-потенциалом.
x=qВh/eа ; qВ=(eа/h)x, (4)
где eа – абсолютная диэлектрическая проницаемость.
Подставляя равенство (4) в формулу (3), получим
v =(eаx/h)Е. (5)
Скорость движения в расчете на единицу напряженности электрического поля называют электрофоретической подвижностью, которая определяется по формуле
vЕ =v/Е (6а)
vЕ =eаx/h (6б)
С учетом формы частиц дисперсной фазы уравнение (5) и (6б) принимает следующий вид:
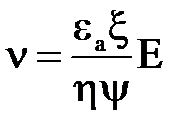 , (7)
, (7)
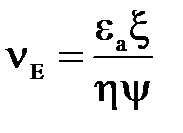 , (8)
, (8)
где v – скорость, м/с; vЕ – электрофоретическая подвижность, м2/(с×В); ψ – коэффициент, зависящий от формы частиц; x - дзета –потенциал, В; Е – напряженность или градиент внешнего электрического поля, В/м.
Коэффициент ψ учитывает форму частиц и их ориентацию в электрическом поле. Для шарообразных частиц коэффициент ψ равен 0,66, а для цилиндрических, ориентированных вдоль силовых линий электрического поля – 1.
Абсолютная диэлектрическая проницаемость среды eа=e·e0, где e - относительная диэлектрическая проницаемость; e0 – абсолютная диэлектрическая проницаемость вакуума, или электрическая постоянная, равная 8,85·10-12 К2/Н·м2 (8,85·10-12 Ф/м) (см. приложение, таблица 5).
С учетом значения абсолютной диэлектрической проницаемости формулу (7) можно представить в виде
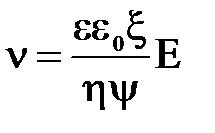 , или
, или 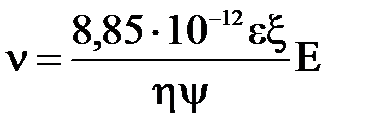 . (9)
. (9)
По формуле (9) находим x-потенциал:
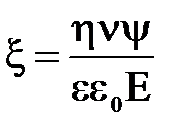 , или
, или 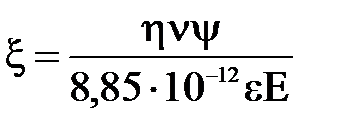 . (10)
. (10)
Согласно формуле (9) величины, которые определяют интенсивность электрофореза и электроосмоса, зависят от свойств среды (h, e), формы частиц (ψ), напряженности внешнего электрического поля (Е) и электрокинетического потенциала (x), определяемого структурой ДЭС.
Электрофоретическую подвижность и электрокинетический потенциал довольно просто определить экспериментально по скорости перемещения дисперсной фазы; электрофоретическая подвижность обычно не превышает 5,0×10-8 м2/(с×В), а электрокинетический потенциал – 100 мВ.
В формулах (7) и (9) не учитывается ряд особенностей дисперсных систем, например электропроводность частиц дисперсной фазы, специфические свойства дисперсной системы в случае ее нахождения в щелях, каналах и капиллярах. Тем не менее, эти формулы являются основными для количественной характеристики электрокинетических явлений.
Дата: 2019-03-05, просмотров: 345.