Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Система линейных алгебраических уравнений (СЛАУ) имеет вид:

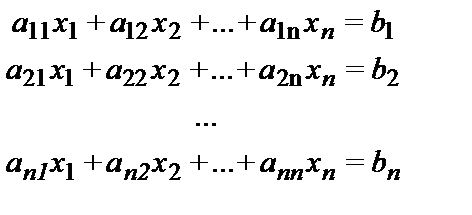
Ее можно представить в матричном виде:

A×X = B

где A - матрица коэффициентов, столбец Х^T=(x₁, x₂, … , x_n) – столбец неизвестных переменных, В^T=(b₁, b₂,…, b_n) - столбец правых частей системы.

Для того, чтобы система могла иметь решение, нужно, чтобы ее определитель не был равен нулю, тогда матрица А — будет невырожденной, а сама система называется совместной.

 

Способы решения СЛАУ.

1. Метод Гаусса.

Он может быть реализован в аналитическом или алгоритмическом виде. Суть аналитического решения по методу Гаусса (МГ):

1) преобразовать СЛАУ к ступенчатому виду – прямой ход МГ;

2) восстановить значения неизвестных переменных с х_n до х₁ –обратный ход МГ.

Алгоритм прямого хода МГ имеет три шага:

1. Проверка a_ii=0. Если условие выполняется, то заменить элементы i-ой и (i+1)-ой строк.

2. Преобразовать элементы i-ой строки так, чтобы a_ii =1, то есть поделить элементы этой строки на a_ii.

3. Все строки с номерами i+1, i+2, …, n преобразовать так, чтобы a_i+1,i , a_i+2,i , … , a_n,i были равны нулю, то есть вычесть последовательно из каждой i+1, i+2, …, n-ой строки i-ую строку, умноженную на a_i+1,i.

 

Пример 2.1:

3x+2y+z=5      (1стр):3            x+2/3y+1/3z=5/3                     (2с)-(1с)

x+y-z=0            ó                 x+y-z=0                      ó

4x-y+5z=3                                      4x-y+5z=3                  (3с)-(1с)*4

x+2/3y+1/3z=5/3                          (2с)*3 x+2/3y+1/3z=5/3 (3с)-(2с)*(-11/3)

1/3y-4/3z=-5/3                      ó      y - 4z = -5                       ó

-11/3y +11/3z=-11/3                    -11/3y +11/3z=-11/3        

 

x+2/3y+1/3z=5/3                     (3с):(-11)         x+2/3y+1/3z=5/3              

 y - 4z = -5                       ó                      y - 4z = -5        ó

 -11z=-22                                                        z=2

 

x+2/3y+1/3z=5/3                     x+2/3*3+1/3*2=5/3                     x=-1

 y-4*2=-5         ó      y=3                              ó      y=3

z=2                              z=2                                         z=2

 

Однако, следует указать недостаток МГ:

Поскольку на каждой ступеньке приходится определять ведущий коэффициент а_ii, то при его значении значительно меньшем единицы, деление на него на шаге 2 приводит к увеличению значений коэффициентов, стоящих в i-ой строке. Причем, чем меньше а_ii, тем сильнее увеличение. Это сказывается на погрешностях расчетов и получаемые значения будут далеки от верных.

Для преодоления недостатка между шагами 1 и 2 вводят дополнительный шаг, заключающийся в выборе максимального из элементов a_i,i, a_i+1,i , a_i+2,i , … , a_n,i. После определения такого максимального элемента, находящегося в k-ой строке,  строчки I и k просто меняют местами. Введение дополнительного шага не сказывается на значениях переменных.

Пример 2.1 с устранением недостатка:

3x+2y+z=5      (1c)<->(3c)      4x-y+5z=3       (1c):4                    

x+y-z=0 ó                                 x+y-z=0            ó                          

4x-y+5z=3                                      3x+2y+z=5          

 

x-1/4y+5/4z=3/4            (2с)-(1с) x-1/4y+5/4z=3/4 (2)<->(3)

x+y-z=0                      ó                      5/4y-9/4z=-3/4            ó

3x+2y+z=5                     (3с)-(1с)*3      11/4y -11/4z=11/4

 

x-1/4y+5/4z=3/4 (2с):(11/4)   x-1/4y+5/4z=3/4      (3с)-(2с)*(5/4)

11/4y -11/4z=11/4  ó            y - z=1           ó

5/4y-9/4z=-3/4                           5/4y-9/4z=-3/4

 

x-1/4y+5/4z=3/4    (3): (-1)         x-1/4y+5/4z=3/4           x=-1

   y - z=1    ó                y-2=1                ó      y=3

        -z=-2                                   z=2                                   z=2

Как видно, решение в обоих случаях одинаковое.

В случае составления программы алгоритм следующий:

1. Для k от 1 до (n-1) выполнить следующее:
2. Для i от (k+1) до n выполнить следующее:
3.        
4.        
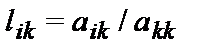
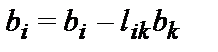
5.          Для j от (k+1) до n выполнить следующее:
6.               
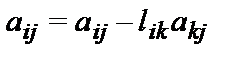
7. Для k от n до 1 выполнить следующее:
8.  

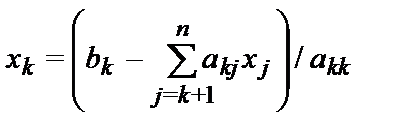
Первые шесть шагов называются прямым ходом метода Гаусса, шаги 7-8- Обратным ходом Метода Гаусса.

Устранение недостатка МГ означает добавление в алгоритм между шагами 1 и 2следующие строчки:

Найти m>=k такое, чтобы |a_mk|=max{|a_ik|} при всех i>=k

Если |a_mk|<eps, то остановить работу (однозначного решения нет), иначе поменять местами b_k и b_m, a_kj и a_mj при k<=j<=n

 

Программа, написанная на языке Pascal , имеет вид:

Uses crt;

Const n1=10;

Var k,i,j,n:integer; sum:real;

l,a,a1:array[1..n1,1..n1] of real;

b,b1,x:array[1..n1] of real;

BEGIN

Write('n=');read(n);

 

{БЛОК ВЫВОДА МАТРИЦЫ A}

For i:=1 to n do

begin

For j:=1 to n do

           begin

                           writeln(‘введите a[',i,',',j,'] элемент');

                          readln(a[i,j]);

    end;

writeln('введите b[',i,'] элемент');

readln(b[i]);

end;

 

{БЛОК ПОКАЗА МАТРИЦЫ А НА ЭКРАНЕ}

writeln(исходная матрица А');

for i:=1 to n do

begin

for j:=1 to n do write(a[i,j],' ');

writeln;

end;

 

{ БЛОК НАХОЖДЕНИЯ МАТРИЦЫ А'=А1}

For k:=1 to n-1 do

For i:=k+1 to n do

  begin

           l[i,k]:=a[i,k]/a[k,k];

           b[i]:=b[i]-l[i,k]*b[k];

           for j:=k+1 to n do a[i,j]:=a[i,j]-l[i,k]*a[k,j];

  end;

For i:=1 to n do

For j:=1 to n do

           begin

           a1[i,j]:=a[i,j]/a[i,i];

           b1[i]:=b[i]/a[i,i];

           end;

 

{БЛОК ПОКАЗА МАТРИЦЫ А1 НА ЭКРАНЕ}

writeln('преобразованная матрица А');

For i:=1 to n do

begin

for j:=1 to n do write(a1[i,j],' ');

writeln;

end;

 

 

{БЛОК РАСЧЕТА МАТРИЦЫ X}

For k:=n downto 1 do

           begin

for j:=k+1 to n do sum:=sum+a1[k,j]*x[j];

x[k]:=b1[k]-sum; sum:=0;

end;

 

{БЛОК ВЫВОДА ПЕРЕМЕННЫХ НА ЭКРАН}

writeln('переменные равны:');

For i:=1 to n do writeln('x[',i,']=',x[i]);

Readln;

END.

 

 

Метод LU разложения матрицы

LU – разложение матрицы – это представление квадратной матрицы А в виде произведения лево-треугольной матрицы L и верхнетреугольной матрицы U. Такое разложение обосновывается следующей теоремой:

Теорема: Любая квадратная матрицы А, главные миноры которой

 отличны от нуля, представима в виде произведения двух матриц A = LU , где

,

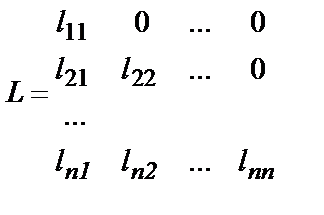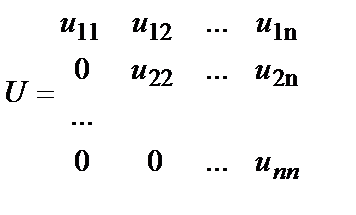
Причем разложение единственно с точностью до диагональных элементов.

 

На практике для удобства элементы u₁₁, u₂₂, …,u_nn принимают равными единице.

После того, как разложение A=LU получено, для нахождения решения СЛАУ можно использовать два шага:

1. Найти набор Y из решения системы L*Y=B (прямой ход МГ)

2. Найти значения переменных Х их решения U*X=Y (обратный ход МГ)

Отметим, что это разложение A=LU помогает тогда, когда требуется найти решение СЛАУ при разных правых частях уравнений.

В случае составления программы алгоритм следующий:

1. L – нулевая матрица, U – единичная.

2. Для i=1..n

3.    Для j=1..n

4.      Если i>=j, то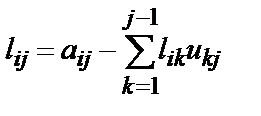

                  иначе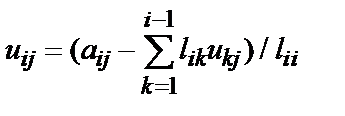

5. Для i=1..n

    

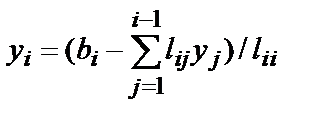
6. Для i=n..1

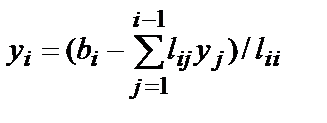
Программа, написанная на языке Pascal , имеет вид:

Uses crt;

Const n1=10;

Var k,i,j,n:integer; l,a,u:array[1..n1,1..n1] of real; b,y,x:array[1..n1] of real; sum:real;

{определяем типы используемых массивов}

BEGIN 

Write(‘n=’);read(n);

 

{БЛОК ВВОДА МАТРИЦЫ А}

For i:=1 to n do

begin

For j:=1 to n do

begin

        write('введите a[',i,',',j,'] '); readln(a[I,j]);

end;

write('введите b[',i,'] ');read(b[i]);

end;

 

 

{БЛОК ПОКАЗА МАТРИЦЫ А НА ЭКРАНЕ}

Writeln(‘Исходная матрица А’);

For i:=1 to n do

begin

For j:=1 to n do write(a[i,j],’ ‘); Writeln;

end;

 

{БЛОК НАХОЖДЕНИЯ МАТРИЦ L и U}

For i:=1 to n do u[i,i]:=1; {матрица U - единичная}

For i:=1 to n do

For j:=1 to n do

   If i>=j then

                          Begin

                                          For k:=1 to j-1 do sum:=sum+l[i,k]*u[k,j];

                                          l[I,j]:=a[I,j]-sum;

                                          sum:=0;

                          end

              else

                          begin

                                          For k:=1 to i-1 do sum:=sum+l[i,k]*u[k,j];

                                          u[i,j]:=(a[i,j]-sum)/l[i,i];

                                          sum:=0;

                          end;

 

{БЛОК ПОКАЗА МАТРИЦЫ L НА ЭКРАНЕ}

Writeln(‘Преобразованная матрица L’);

For i:=1 to n do

begin

For j:=1 to n do write(l[i,j],’ ‘);

Writeln;

End;

 

{БЛОК ПОКАЗА МАТРИЦЫ U НА ЭКРАНЕ}

Writeln(‘Преобразованная матрица U’)

For i:=1 to n do

begin

For j:=1 to n do write(u[i,j],’ ‘);

Writeln;

End;

{БЛОК ПОДСЧЕТА И ПОКАЗА ПЕРЕМЕННЫХ Y}

For i:=1 to n do

           Begin

           For j:=1 to i-1 do sum:= sum+l[i,j]*y[j];

           Y[i]:=(b[i]-sum)/l[I,i]; writeln(‘y[’,I,’]=’,y[i]);

           Sum:=0;

           End;

 

{БЛОК ПОДСЧЕТА И ПОКАЗА ПЕРЕМЕННЫХ X}

For i:=n downto 1 do

           begin

 For j:=i+1 to n do sum:=sum+u[i,j]*x[j];

X[i]:=y[i]-sum;

writeln(‘x[’,i,’]=’,x[i]);

sum:=0;

End;  

Readln;

END.

Пример 2.2:

Дана матрица А. Найти элементы матриц L и U.

           3        2        1

A=     1        1        -1

           4        -1       5

Решение:         0        0        0                        1        0        0

1.Пусть L=      0        0        0,    U=         0        1        0

                          0        0        0                        0        0        1

2.i=1

3. j=1

4. 1>=1 then l₁₁=a₁₁=3

3.j=2

4. 1>=2 else u₁₂=(a₁₂-0)/l₁₁ = 2/3

 

3.j=3

4. 1>=3 else u₁₃=(a₁₃-0)/l₁₁ = 1/3

2.i=2

3. j=1

4. 2>=1 then l₂₁=a₂₁=1

3.j=2

4. 2>=2 then l₂₂=a₂₂-l₂₁*u₁₂ = 1/3

3.j=3

4. 2>=3 else u₂₃=(a₂₃-l₂₁*u₁₃)/l₂₂ = -4

2.i=3

3. j=1

4. 3>=1 then l₃₁=a₃₁=4

3.j=2

4. 3>=2 then l₃₂=a₃₂-l₃₁*u₁₂ = -11/3

3.j=3

4. 3>=3 then l₃₃=(a₃₃-l₃₁*u₁₃-l₃₂*u₂₃) = -11

 

Таким образом, получены матрицы 

           3        0        0                        1        2/3     1/3

 L=     1        1/3     0,     U=        0        1        -4

           4        -11/3 -11                    0        0        1

 

5.i=1  y₁=b₁/l₁₁=5/3

5.i=2  y₂=(b₂-l₂₁*y1)/l₂₂=(0-1*5/3)/ 1/3 = -5

5.i=3  y₃=(b₃-l₃₁*y1-l₃₂*y2)/l₃₃ = (3-4*5/3-(-11/3)*(-5))/(-11) = 2

Таким образом, получен столбец Y=(5/3, -5, 2)

 

6.i=3  x₃=y₃=2

6.i=2  x₂=(y₂-u₂₃*x₃)=(-5-(-4)*2)=3

6.i=1  x₁=(y₁-u₁₂*x₂-u₁₃*x₃)=5/3-2/3*3-1/3*2=-1

Таким образом, получены неизвестные х₁=-1, х₂ = 3, х₃ = 2.

3. Нахождение обратной матрицы методом Гаусса

Ненулевая матрица А называется обратимой, если существует матрица А^-1, называемая обратной, и выполнено условие:

А^-1∙А = А∙А^-1 = Е

Пусть Х – обратная матрица, тогда А∙Х = Е. Представляя матрицы Х и Е в виде х_i=(x_1i x_2i … x_ni)^T и е_i=(0 … 1 … 0)^Т, получим n систем

A∙x_i = e_i, где 1<=i<=n,

где в качестве неизвестных векторов выступают столбцы искомой матрицы Х, а в качестве известных векторов правой части системы – поочередно столбцы единичной матрицы. Разложение матрицы А достаточно сделать один раз.

Пример 2.3:

Дана матрица А. Найти обратную к ней.

           3        2        1

A=     1        1        -1

           4        -1       5

Решение:

Приведем аналитическое решение.

Итак, необходимо решить три системы (количество решаемых систем равно порядку исходной матрицы, n=3) любым удобным способом.

 

1) 3x₁₁+2x₂₁+x₃₁=1                        x₁₁+2/3x₂₁+1/3x₃₁=1/3

  x₁₁+ x₂₁ – x₃₁=0        ó      x₁₁+ x₂₁ - x₃₁=0         ó          

4x₁₁ – x₂₁+5x₃₁=0                      4x₁₁ - x₃₁ + 5x₃₁=0                           

 

x₁₁+2/3x₂₁+1/3x₃₁=1/3             x₁₁+2/3x₂₁+1/3x₃₁=1/3

1/3x₂₁ - 4/3x₃₁=-1/3       ó      x₂₁  - 4x₃₁=-1             ó

-11/3x₂₁+11/3x₃₁=-4/3            -11/3x₂₁+11/3x₃₁=-4/3      

 

x₁₁+2/3x₂₁+1/3x₃₁=1/3             x₁₁+2/3x₂₁+1/3x₃₁=1/3  x₁₁=-4/11

 x₂₁  - 4x₃₁=-1            ó      x₂₁  - 4x₃₁=-1                  x₂₁=9/11

 -11x₃₁= -5                                  x₃₁=5/11                                 x₃₁=5/11

 

2) 3x₁₂+2x₂₂+x₃₂=0                        x₁₂+2/3x₂₂+1/3x₃₂=0          

  x₁₂+ x₂₂ – x₃₂=1         ó      x₁₂+ x₂₂ - x₃₂=1         ó          

4x₁₂ – x₂₂+5x₃₂=0                      4x₁₂ - x₃₂ +  5x₃₂=0                           

 

x₁₂+2/3x₂₂+1/3x₃₂=0                 x₁₂+2/3x₂₂+1/3x₃₂=0          

1/3x₂₂ - 4/3x₃₂=1            ó      x₂₂  - 4x₃₂=3                  ó

-11/3x₂₂+11/3x₃₂=0                  -11/3x₂₂+11/3x₃₂=0                           

 

x₁₂+2/3x₂₂+1/3x₃₂=0                     x₁₂+2/3x₂₂+1/3x₃₂=0      x₁₂=1

 x₂₂  - 4x₃₂=1               ó      x₂₂  - 4x₃₂=3                  x₂₂=-1

-11x₃₂= 11                                  x₃₂=-1                         x₃₂=-1

 

3) 3x₁₃+2x₂₃+x₃₃=0                        x₁₃+2/3x₂₃+1/3x₃₃=0          

  x₁₃+ x₂₃ – x₃₃=0        ó      x₁₃+ x₂₃ - x₃₃=0         ó          

4x₁₃ – x₂₃+5x₃₃=1                      4x₁₃ - x₃₃ + 5x₃₃=1                           

 

x₁₃+2/3x₂₃+1/3x₃₃=0                 x₁₃+2/3x₂₃+1/3x₃₃=0          

  1/3x₂₃ - 4/3x₃₃=0     ó                 x₂₃  - 4x₃₃=0        ó          

-11/3x₂₃+11/3x₃₃=1              -11/3x₂₃+11/3x₃₃=1                       

 

x₁₃+2/3x₂₃+1/3x₃₃=0                     x₁₃+2/3x₂₃+1/3x₃₃=0      x₁₃=3/11

       x₂₃  - 4x₃₃=0       ó      x₂₃  - 4x₃₃=0  x₂₃=-4/11

               -11x₃₃= 1                     x₃₃=-1/11                    x₃₃=-1/11

 

Таким образом, обратная матрица к матрице A имеет вид:

                          -4/11 1        3/11

X=     9/11  -1       -4/11

           5/11  -1       -1/11

 

Проверка: А∙Х = Е

 

3   2 1              -4/11 1 3/11                1 0 0

1 1 -1 ×       9/11 -1 -4/11 =        0 1 0

4 -1 5              5/11 -1 -1/11                0 0 1

В случае составления программы алгоритм следующий:

1. Для z от 1 до n выполнить следующее:
2. b[z,z]=1
3.   Для k от 1 до (n-1) выполнить следующее:
4.     Для i от (k+1) до n выполнить следующее:
5.        
6.        
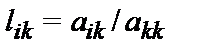
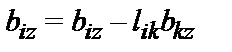
7.          Для j от (k+1) до n выполнить следующее:
8.               

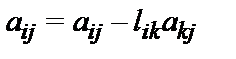
1. Для k от n до 1 выполнить следующее:

9.   

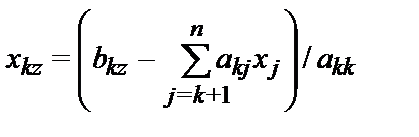
Программа, написанная на языке Pascal , имеет вид:

Uses crt;

Const n1=10;

Var z,k,i,j,n:integer;

l,a,x,b,a1,b1:array[1..n1,1..n1] of real;

sum:real;

BEGIN clrscr;

write('n=');read(n);

For i:=1 to n do

For j:=1 to n do

           begin

Write('vvedite a[',i,',',j,']=');

readln(a[i,j]);

                          end;

Writeln(' matrix À');

For i:=1 to n do

Begin

For j:=1 to n do write(a[i,j],' ');

Writeln;

End;

For z:=1 to n do b[z,z]:=1;

For k:=1 to n-1 do

        For i:=k+1 to n do

                   Begin

                        l[i,k]:=a[i,k]/a[k,k];

                        for z:=1 to n do b[i,z]:=b[i,z]-l[i,k]*b[k,z];

                        For j:=k+1 to n do a[i,j]:=a[i,j]-l[i,k]*a[k,j];

                   End;

For i:=1 to n do

For j:=1 to n do

           Begin

           A1[i,j]:=a[i,j]/a[i,i];

  for z:=1 to n do B1[i,z]:=b[i,z]/a[I,i];

end;

for z:=1 to n do

For k:=n downto 1 do

begin

For j:=k+1 to n do sum:=sum+a1[k,j]*x[j,z];

x[k,z]:=(b1[k,z]-sum)/a1[k,k]; sum:=0;

                                          end;

writeln;

Writeln('matrix À^(-1)');

For i:=1 to n do

begin

For j:=1 to n do write(x[i,j],' ');

Writeln;

end;

Readln;

END.