Стерлитамакский филиал
Федерального государственного бюджетного образовательного учреждения высшего образования
«Башкирский государственный университет»
Гиззатова Э.Р., Борисевич С.С., Гнатенко Ю.А.
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА.
МЕТОДЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ:
Учебное пособие
для студентов, обучающихся по направлениям
04.03.01 Химия и 03.03.02 Физика.
Стерлитамак 2016
УДК 519.6
ББК 22.192я73
Г 46
Гиззатова Э.Р., Борисевич С.С., Гнатенко Ю.А. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА. МЕТОДЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ: учебное пособие.
Учебное пособие содержит тематический материал по основным разделам вычислительной математики, методам математической обработки информации, численным методам. Представление ведется по темам, состоящим из теоретической и практической частей. В первой из них раскрываются понятия, термины раздела, приводятся формулировки теорем. Вторая часть темы – это примеры и типовые задачи с решениями, полученными в прикладных программных обеспечениях и математических пакетах, а также задания для лабораторных работ. Пособие предназначено для студентов, обучающихся по направлению «Химия» и «Физика», и может быть использовано в качестве дополнительного материала преподавателями..
Ответственный редактор – кандидат физико-математических наук, доцент А.И. Карамова (Стерлитамакский филиал ФГБОУ ВО «БашГУ»)
Рецензенты:
кандидат технических наук Т.М. Левина (филиал ФГБОУ ВО УГНТУ в г. Салавате); кафедра математического моделирования (Стерлитамакский филиал ФГБОУ ВО БашГУ); кафедра «Общенаучных дисциплин» (филиал ФГБОУ ВО УГНТУ в г. Салавате).
© Э.Р. Гиззатова, С.С. Борисевич, Ю.А. Гнатенко, 2016
ТЕМА 1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И ПОГРЕШНОСТИ
Процесс решения задач из физики, техники, экономики или химии с помощью методов математического моделирования состоит из нескольких этапов, показанных на рисунке:
| 1. Исследование объекта и содержательная постановка задачи |
| 2. Построение математической модели |
| 3. Выбор численного метода и разработка вычислительного алгоритма |
| 4. Разработка программы на компьютере или выбор пакета прикладных программ |
| 5. Проведение вычислений и анализ результатов |
1. На первом этапе проводится исследование объекта и формулируется содержательная (физическая, техническая, экономическая, химическая и др.) постановка задачи. Для того, чтобы задачу можно было описать количественно, нужно провести качественный и количественный анализ свойств объекта и выделить основные параметры, оказывающие на них наиболее существенное влияние.
2. Следующим этапом является математическая постановка задачи, в процессе которой осуществляется построение математической модели объекта. Под математической моделью понимают систему математических соотношений (уравнений, неравенств, краевых, начальных условий), которым должна удовлетворять система основных параметров задачи или объекта. Одно из основных требований, предъявляемых к математической модели – соответствие исследуемому объекту, т.е. адекватность. Другое немаловажное требование – чтобы модель была не слишком сложной, доступной для математической обработки. Умение находить оптимальное сочетание адекватности и сложности зависит от квалификации и даже интуиции исследователя.
3. На следующем этапе необходимо найти методы (алгоритмы) решения математической задачи. В наиболее простых случаях удается построить аналитическое решение задачи. Такие решения являются наиболее привлекательными, поскольку позволяют не только количественно, но и, что не менее важно, качественно проанализировать исследуемые параметры. Но в подавляющем большинстве случаев это не представляется возможным, и для решения математической задачи применяются численные методы. На следующем рисунке приведена классификация методов решения вычислительных задач:
| Методы решения вычислительных задач |
| Аналитические |
| Численные |
| Приближенные |
| Точные |
| Алгоритмы |
| Итерационные |
| Прямые |
4. Четвертым этапом является разработка программы решения задачи на компьютере, ее тестирование и отладка. Возможно, что рассматриваемая математическая задача исследована, и для ее решения разработаны стандартные программы, которые могут существовать отдельно или входить в пакеты прикладных программ.
5. На заключительном этапе выполняют вычислительные эксперименты на компьютере и проводят анализ результатов. Если результаты не удовлетворяют исследователя, требуется совершенствование алгоритма или метода решения задачи, ее математической модели, а в некоторых случаях – корректировка содержательной постановки.
Значащие цифры
Значащими цифрами в записи приближенного числа называются:
- все ненулевые цифры;
- нули, содержащиеся между ненулевыми цифрами;
- нули, являющиеся представителями сохраненных десятичных разрядов при округлении.
Первые n значащих цифр в записи приближенного числа называются верными в узком смысле, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего п-й значащей цифре, считая слева направо.
Иногда это определение перефразируют:
Первые n значащих цифр в записи приближенного числа называются верными в широком смысле, если абсолютная погрешность числа не превосходит единицы разряда, соответствующего n – ой значащей цифре.
Пример 1.3.
Определить значащие цифры в записи чисел:
а) ар=2,4537, Dа=0,02539;
б) ар=0,03278, Dа=0,02539;
в) ар=27080, Dа=1245.
Решение
а) Выпишем значение абсолютной погрешности в виде формулы (*):
Dа = 0,03 = 3×10-2
Тогда ар = 2,46 и можно определить верную запись для величины а как а = 2,46 ± 0,03, однако, если приближенное число ар является промежуточным результатом, то оставляют погрешность в виде (**):
Dа = 0,025 = 2,5×10-2
и запись величины а будет иметь вид: а = 2,454 ± 0,025.
б) при решении этого пункта сразу будем выписывать абсолютную погрешность числа в виде формулы (**), поскольку видно, что и само число ар, и его погрешность – числа одного порядка:
Dа = 0,025 = 2,5×10-2
Такой результат, когда и приближенное число, и его погрешность сравнимы, свидетельствует, что число найдено очень грубо. В таких случаях иногда требуется проведение дополнительных исследований для уменьшения значения абсолютной погрешности.
Тогда верная запись числа будет следующей: ар = 0,033, а истинную величину а можно записать как: а = 0,033 ± 0,025 = (3,3 ± 2,5) ×10-2.
Последняя запись наиболее логична, поскольку сразу иллюстрирует, как соотносятся друг с другом число и погрешность.
в) Выпишем абсолютную погрешность в виде формулы (*):
Dа = 1000 = 1×103
Тогда приближенное число будет равно ар = 27000 и запись величины а верными знаками а = 27000 ± 1000 = (2,7 ± 0,1) ×104.
И в этом пункте в), и в предыдущих использованы правила округления.
Пример 1.4.
Определить абсолютные погрешности приближенных чисел с предположением о том, что:
а) ар=2,453 записано верными знаками в широком смысле;
б) ар=27080 записано верными знаками в узком смысле.
Решение
а) предположение о записи числа с верными знаками в широком смысле означает, что абсолютная погрешность числа не превосходит единицы разряда, соответствующего последней значащей цифре, тогда, зная что, цифра «3» находится в третьем знаке после запятой, абсолютной погрешности будет равна:
Dа = 0,001 = 1×10-3
И верная запись числа а = 2,453 ± 0,001
б) иная запись числа – с верными знаками в узком смысле, тогда абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего последней значащей цифре, считая слева направо. Так как последняя ненулевая цифра находится в разряде десятка, то за абсолютную погрешность числа можно принять Dа = 0,5×10 = 5.
Значит, запись величины а будет иметь вид: а = 27080 ± 5.
Правила округления чисел
Чтобы округлить число до n значащих цифр, отбрасывают все цифры, стоящие справа от n-й значащей цифры, или, если это нужно для сохранения разрядов, заменяют их нулями. При этом:
1) если первая отброшенная цифра меньше 5, то оставшиеся десятичные знаки сохраняют без изменения;
2) если первая отброшенная цифра больше 5, то к последней оставшейся цифре прибавляют единицу;
3) если первая отброшенная цифра равна 5 и среди остальных отброшенных цифр есть ненулевые, то к последней оставшейся цифре прибавляют единицу;
4) если первая из отброшенных цифр равна 5 и все отброшенные цифры являются нулями, то последняя оставшаяся цифра оставляется неизменной, если она четная, и увеличивается на единицу, если нечетная (правило четной цифры).
Это правило гарантирует, что сохраненные значащие цифры числа являются верными в узком смысле, т. е. погрешность округления не превосходит половины разряда, соответствующего последней оставленной значащей цифре. Правило четной цифры должно обеспечить компенсацию знаков ошибок.
Пример 1.5.
Округлить числа ар до указанных разрядов:
а) ар=2453,2 до разряда сотен;
б) ар=2,7080 до разряда сотых;
в) ар = 34,150 до разряда десятых.
Решение
а) для решения используем правило 3, так как первая отброшенная цифра «3» больше нуля, значит, ар = 2460.
б) для решения воспользуется правилом 2, тогда ар = 2,71.
в) в этом случае необходимо воспользоваться правилом 4, так как первая отброшенная цифра равна 5, а за ней следует число «0», при этом до цифры «5», стоит «1» - нечетное число, следовательно:
ар = 34,2.
Иногда требуется оценить погрешность числа, не проводя дополнительных испытаний, тогда можно использовать следующую теорему.
Теорема. Если положительное приближенное число имеет n верных значащих цифр, то его относительная погрешность δ не превосходит величины 101-n, деленной на первую значащую цифру a1:
δ £ 101-n / a1
Эта формула позволяет вычислить предельную относительную погрешность
δa = 101-n / a1
Пример 1.6.
Определить абсолютные и относительные погрешности следующих чисел:
а) ар=24,2;
б) ар=27000.
Решение
а) здесь aн = 2, а количество ненулевых значащих разрядов равно 3, то за δa можно принять величину:
δa = 101-3 / 2 = 0,005
тогда Dа = 0,005 × 24,2 = 0,121 » 0,1.
б)в данном случае aн = 2, а количество ненулевых значащих разрядов равно 2, то за δa можно принять величину:
δa = 101-2 / 2 = 0,05
тогда Dа = 0,05 × 27000 = 1350 » 1000.
Задание 1.
Вычислить погрешности следующих величин:
а) выписать абсолютную погрешность приближенного числа в виде формулы (*) и (**) Da = 0,02N31;
б) округлить число ар = 1,3N56, если абсолютная погрешность найдена двумя способами в п. а);
в) оценить (выписать через знак «±» ) величину а двумя способами, согласно решению, найденному в п б);
г)определить относительную погрешность числа ар, если абсолютная погрешность найдена по двум формулам (*) и (**) в п. а).
Задание 2.
Округлить числа:
а) ар = 23,4N4 до сотых;
б) ар = 0,0N50 до тысячных;
в) ар = 23N0N до разряда сотен.
г) ар = 23,4N4 при Da = 0,24;
д) ар = 2,N при Da = 0,03;
Задание 3.
Определить погрешность чисел:
а) ар = 3,4N в предположении, что оно записано верными цифрами в широком смысле;
б) ар = 3,4N в предположении, что оно записано верными цифрами в узком смысле.
Задание 4.
Рассчитать сумму и вычислить абсолютную погрешность; оценить сумму чисел:
Х1 = 0,N43 X2 = -3, 0N X3 = 2,N X4 = 1,03.
Задание 5.
Вычислить погрешности одномерной функции y= y ( x ) по формулам (1.1)–(1.4). Провести сравнительный анализ полученных погрешностей.
а) 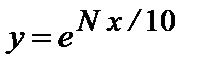 , на промежутке [-2.0;-1.8], D x *=0.01,
, на промежутке [-2.0;-1.8], D x *=0.01,
х*=-1.9+ N /100.
б) 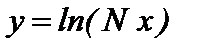 , на промежутке [2;3], D x *=0.05, х*=2.52+ N/1000 .
, на промежутке [2;3], D x *=0.05, х*=2.52+ N/1000 .
в) 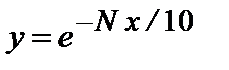 , на промежутке [3;3.2], D x *=0. 0 1,
, на промежутке [3;3.2], D x *=0. 0 1,
х*=3.1 5-N/1000 .
г) 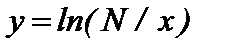 , на промежутке [2;4], D x *= 0,2 , х*= 2,56+N/100 .
, на промежутке [2;4], D x *= 0,2 , х*= 2,56+N/100 .
Задание 6 .
Вычислить погрешности двумерной функции z= z ( x , y ) по формулам (1.1)–(1.4). Провести сравнительный анализ полученных погрешностей.
а) 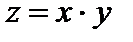 , G =[- N ;- N +1]×[1.2;1.4], D x *=0. 0 5, х*=- N +0. 28 , D y *=0. 0 1, y *=1.3 7 .
, G =[- N ;- N +1]×[1.2;1.4], D x *=0. 0 5, х*=- N +0. 28 , D y *=0. 0 1, y *=1.3 7 .
б) 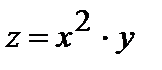 , G =[2;2.4]×[ N /2; N /2 + 1], D x *=0. 0 2,
, G =[2;2.4]×[ N /2; N /2 + 1], D x *=0. 0 2,
х*=2. 3 2 +N/1000 , D y *=0. 05 , y *=( N +1)/2 +N/1000 .
в) 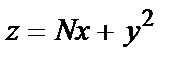 , G =[1.0;1.6]×[0.8;1.0], D x *=0. 03 , х*=1 ,36-N/100 , D y *=0. 0 1, y *=0. 87 .
, G =[1.0;1.6]×[0.8;1.0], D x *=0. 03 , х*=1 ,36-N/100 , D y *=0. 0 1, y *=0. 87 .
г) 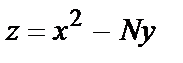 , G =[1.2;1. 6 ]×[2.0;2.4], D x *=0. 02 , х*=1. 3+N/100 , D y *=0. 0 2, y *=2.2 45 .
, G =[1.2;1. 6 ]×[2.0;2.4], D x *=0. 02 , х*=1. 3+N/100 , D y *=0. 0 2, y *=2.2 45 .
Контрольные вопросы
1. Перечислите этапы решения прикладной задачи.
2. Какие причины погрешностей бывают?
3. Приведите формулу, связывающую абсолютную и относительную погрешности.
4. В чем отличие абсолютной погрешности от абсолютной предельной погрешности.
5. Какие цифры в записи числа называют верными и значащими?
6. Приведите правила округления чисел.
7. Как вычислить предельную абсолютную погрешность суммы чисел?
8. Как вычислить предельную относительную погрешность произведения?
9. Как рассчитать предельную абсолютную погрешность одномерной функции?
10. Как рассчитать предельную абсолютную погрешность двумерной функции?
Способы решения СЛАУ.
- Метод Гаусса.
Он может быть реализован в аналитическом или алгоритмическом виде. Суть аналитического решения по методу Гаусса (МГ):
1) преобразовать СЛАУ к ступенчатому виду – прямой ход МГ;
2) восстановить значения неизвестных переменных с хn до х1 –обратный ход МГ.
Алгоритм прямого хода МГ имеет три шага:
1. Проверка aii=0. Если условие выполняется, то заменить элементы i-ой и (i+1)-ой строк.
2. Преобразовать элементы i-ой строки так, чтобы aii =1, то есть поделить элементы этой строки на aii.
3. Все строки с номерами i+1, i+2, …, n преобразовать так, чтобы ai+1,i , ai+2,i , … , an,i были равны нулю, то есть вычесть последовательно из каждой i+1, i+2, …, n-ой строки i-ую строку, умноженную на ai+1,i.
Пример 2.1:
3x+2y+z=5 (1стр):3 x+2/3y+1/3z=5/3 (2с)-(1с)
x+y-z=0 ó x+y-z=0 ó
4x-y+5z=3 4x-y+5z=3 (3с)-(1с)*4
x+2/3y+1/3z=5/3 (2с)*3 x+2/3y+1/3z=5/3 (3с)-(2с)*(-11/3)
1/3y-4/3z=-5/3 ó y - 4z = -5 ó
-11/3y +11/3z=-11/3 -11/3y +11/3z=-11/3
x+2/3y+1/3z=5/3 (3с):(-11) x+2/3y+1/3z=5/3
y - 4z = -5 ó y - 4z = -5 ó
-11z=-22 z=2
x+2/3y+1/3z=5/3 x+2/3*3+1/3*2=5/3 x=-1
y-4*2=-5 ó y=3 ó y=3
z=2 z=2 z=2
Однако, следует указать недостаток МГ:
Поскольку на каждой ступеньке приходится определять ведущий коэффициент аii, то при его значении значительно меньшем единицы, деление на него на шаге 2 приводит к увеличению значений коэффициентов, стоящих в i-ой строке. Причем, чем меньше аii, тем сильнее увеличение. Это сказывается на погрешностях расчетов и получаемые значения будут далеки от верных.
Для преодоления недостатка между шагами 1 и 2 вводят дополнительный шаг, заключающийся в выборе максимального из элементов ai,i, ai+1,i , ai+2,i , … , an,i. После определения такого максимального элемента, находящегося в k-ой строке, строчки I и k просто меняют местами. Введение дополнительного шага не сказывается на значениях переменных.
Пример 2.1 с устранением недостатка:
3x+2y+z=5 (1c)<->(3c) 4x-y+5z=3 (1c):4
x+y-z=0 ó x+y-z=0 ó
4x-y+5z=3 3x+2y+z=5
x-1/4y+5/4z=3/4 (2с)-(1с) x-1/4y+5/4z=3/4 (2)<->(3)
x+y-z=0 ó 5/4y-9/4z=-3/4 ó
3x+2y+z=5 (3с)-(1с)*3 11/4y -11/4z=11/4
x-1/4y+5/4z=3/4 (2с):(11/4) x-1/4y+5/4z=3/4 (3с)-(2с)*(5/4)
11/4y -11/4z=11/4 ó y - z=1 ó
5/4y-9/4z=-3/4 5/4y-9/4z=-3/4
x-1/4y+5/4z=3/4 (3): (-1) x-1/4y+5/4z=3/4 x=-1
y - z=1 ó y-2=1 ó y=3
-z=-2 z=2 z=2
Как видно, решение в обоих случаях одинаковое.
В случае составления программы алгоритм следующий:
- Для k от 1 до (n-1) выполнить следующее:
- Для i от (k+1) до n выполнить следующее:
-
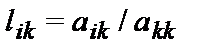
-
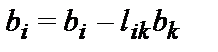
- Для j от (k+1) до n выполнить следующее:
-
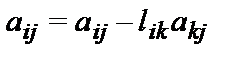
- Для k от n до 1 выполнить следующее:
-
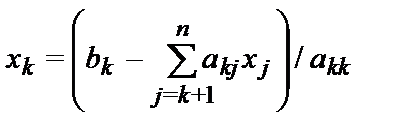
Первые шесть шагов называются прямым ходом метода Гаусса, шаги 7-8- Обратным ходом Метода Гаусса.
Устранение недостатка МГ означает добавление в алгоритм между шагами 1 и 2следующие строчки:
Найти m>=k такое, чтобы |amk|=max{|aik|} при всех i>=k
Если |amk|<eps, то остановить работу (однозначного решения нет), иначе поменять местами bk и bm, akj и amj при k<=j<=n
Программа, написанная на языке Pascal , имеет вид:
Uses crt;
Const n1=10;
Var k,i,j,n:integer; sum:real;
l,a,a1:array[1..n1,1..n1] of real;
b,b1,x:array[1..n1] of real;
BEGIN
Write('n=');read(n);
{БЛОК ВЫВОДА МАТРИЦЫ A}
For i:=1 to n do
begin
For j:=1 to n do
begin
writeln(‘введите a[',i,',',j,'] элемент');
readln(a[i,j]);
end;
writeln('введите b[',i,'] элемент');
readln(b[i]);
end;
{БЛОК ПОКАЗА МАТРИЦЫ А НА ЭКРАНЕ}
writeln(исходная матрица А');
for i:=1 to n do
begin
for j:=1 to n do write(a[i,j],' ');
writeln;
end;
{ БЛОК НАХОЖДЕНИЯ МАТРИЦЫ А'=А1}
For k:=1 to n-1 do
For i:=k+1 to n do
begin
l[i,k]:=a[i,k]/a[k,k];
b[i]:=b[i]-l[i,k]*b[k];
for j:=k+1 to n do a[i,j]:=a[i,j]-l[i,k]*a[k,j];
end;
For i:=1 to n do
For j:=1 to n do
begin
a1[i,j]:=a[i,j]/a[i,i];
b1[i]:=b[i]/a[i,i];
end;
{БЛОК ПОКАЗА МАТРИЦЫ А1 НА ЭКРАНЕ}
writeln('преобразованная матрица А');
For i:=1 to n do
begin
for j:=1 to n do write(a1[i,j],' ');
writeln;
end;
{БЛОК РАСЧЕТА МАТРИЦЫ X}
For k:=n downto 1 do
begin
for j:=k+1 to n do sum:=sum+a1[k,j]*x[j];
x[k]:=b1[k]-sum; sum:=0;
end;
{БЛОК ВЫВОДА ПЕРЕМЕННЫХ НА ЭКРАН}
writeln('переменные равны:');
For i:=1 to n do writeln('x[',i,']=',x[i]);
Readln;
END.
Метод LU разложения матрицы
LU – разложение матрицы – это представление квадратной матрицы А в виде произведения лево-треугольной матрицы L и верхнетреугольной матрицы U. Такое разложение обосновывается следующей теоремой:
Теорема: Любая квадратная матрицы А, главные миноры которой
отличны от нуля, представима в виде произведения двух матриц A = LU , где
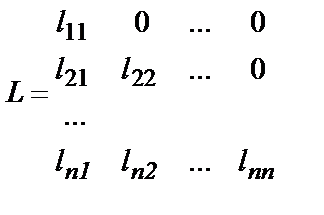 ,
, 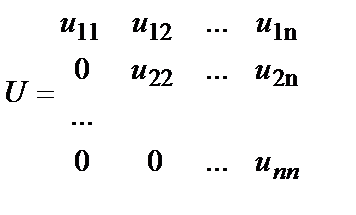
Причем разложение единственно с точностью до диагональных элементов.
На практике для удобства элементы u11, u22, …,unn принимают равными единице.
После того, как разложение A=LU получено, для нахождения решения СЛАУ можно использовать два шага:
1. Найти набор Y из решения системы L*Y=B (прямой ход МГ)
2. Найти значения переменных Х их решения U*X=Y (обратный ход МГ)
Отметим, что это разложение A=LU помогает тогда, когда требуется найти решение СЛАУ при разных правых частях уравнений.
В случае составления программы алгоритм следующий:
1. L – нулевая матрица, U – единичная.
2. Для i=1..n
3. Для j=1..n
4. Если i>=j, то 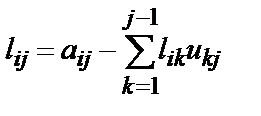

иначе 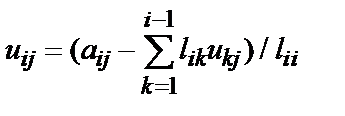
5. Для i=1..n
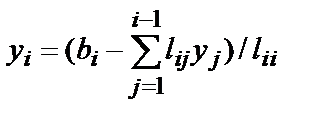
6. Для i=n..1
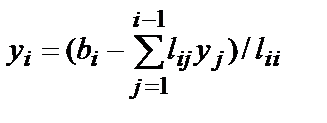
Программа, написанная на языке Pascal , имеет вид:
Uses crt;
Const n1=10;
Var k,i,j,n:integer; l,a,u:array[1..n1,1..n1] of real; b,y,x:array[1..n1] of real; sum:real;
{определяем типы используемых массивов}
BEGIN
Write(‘n=’);read(n);
{БЛОК ВВОДА МАТРИЦЫ А}
For i:=1 to n do
begin
For j:=1 to n do
begin
write('введите a[',i,',',j,'] '); readln(a[I,j]);
end;
write('введите b[',i,'] ');read(b[i]);
end;
{БЛОК ПОКАЗА МАТРИЦЫ А НА ЭКРАНЕ}
Writeln(‘Исходная матрица А’);
For i:=1 to n do
begin
For j:=1 to n do write(a[i,j],’ ‘); Writeln;
end;
{БЛОК НАХОЖДЕНИЯ МАТРИЦ L и U}
For i:=1 to n do u[i,i]:=1; {матрица U - единичная}
For i:=1 to n do
For j:=1 to n do
If i>=j then
Begin
For k:=1 to j-1 do sum:=sum+l[i,k]*u[k,j];
l[I,j]:=a[I,j]-sum;
sum:=0;
end
else
begin
For k:=1 to i-1 do sum:=sum+l[i,k]*u[k,j];
u[i,j]:=(a[i,j]-sum)/l[i,i];
sum:=0;
end;
{БЛОК ПОКАЗА МАТРИЦЫ L НА ЭКРАНЕ}
Writeln(‘Преобразованная матрица L’);
For i:=1 to n do
begin
For j:=1 to n do write(l[i,j],’ ‘);
Writeln;
End;
{БЛОК ПОКАЗА МАТРИЦЫ U НА ЭКРАНЕ}
Writeln(‘Преобразованная матрица U’)
For i:=1 to n do
begin
For j:=1 to n do write(u[i,j],’ ‘);
Writeln;
End;
{БЛОК ПОДСЧЕТА И ПОКАЗА ПЕРЕМЕННЫХ Y}
For i:=1 to n do
Begin
For j:=1 to i-1 do sum:= sum+l[i,j]*y[j];
Y[i]:=(b[i]-sum)/l[I,i]; writeln(‘y[’,I,’]=’,y[i]);
Sum:=0;
End;
{БЛОК ПОДСЧЕТА И ПОКАЗА ПЕРЕМЕННЫХ X}
For i:=n downto 1 do
begin
For j:=i+1 to n do sum:=sum+u[i,j]*x[j];
X[i]:=y[i]-sum;
writeln(‘x[’,i,’]=’,x[i]);
sum:=0;
End;
Readln;
END.
Пример 2.2:
Дана матрица А. Найти элементы матриц L и U.
3 2 1
A= 1 1 -1
4 -1 5
Решение: 0 0 0 1 0 0
1.Пусть L= 0 0 0, U= 0 1 0
0 0 0 0 0 1
2.i=1
3. j=1
4. 1>=1 then l11=a11=3
3.j=2
4. 1>=2 else u12=(a12-0)/l11 = 2/3
3.j=3
4. 1>=3 else u13=(a13-0)/l11 = 1/3
2.i=2
3. j=1
4. 2>=1 then l21=a21=1
3.j=2
4. 2>=2 then l22=a22-l21*u12 = 1/3
3.j=3
4. 2>=3 else u23=(a23-l21*u13)/l22 = -4
2.i=3
3. j=1
4. 3>=1 then l31=a31=4
3.j=2
4. 3>=2 then l32=a32-l31*u12 = -11/3
3.j=3
4. 3>=3 then l33=(a33-l31*u13-l32*u23) = -11
Таким образом, получены матрицы
3 0 0 1 2/3 1/3
L= 1 1/3 0, U= 0 1 -4
4 -11/3 -11 0 0 1
5.i=1 y1=b1/l11=5/3
5.i=2 y2=(b2-l21*y1)/l22=(0-1*5/3)/ 1/3 = -5
5.i=3 y3=(b3-l31*y1-l32*y2)/l33 = (3-4*5/3-(-11/3)*(-5))/(-11) = 2
Таким образом, получен столбец Y=(5/3, -5, 2)
6.i=3 x3=y3=2
6.i=2 x2=(y2-u23*x3)=(-5-(-4)*2)=3
6.i=1 x1=(y1-u12*x2-u13*x3)=5/3-2/3*3-1/3*2=-1
Таким образом, получены неизвестные х1=-1, х2 = 3, х3 = 2.
3. Нахождение обратной матрицы методом Гаусса
Ненулевая матрица А называется обратимой, если существует матрица А-1, называемая обратной, и выполнено условие:
А-1∙А = А∙А-1 = Е
Пусть Х – обратная матрица, тогда А∙Х = Е. Представляя матрицы Х и Е в виде хi=(x1i x2i … xni)T и еi=(0 … 1 … 0)Т, получим n систем
A∙xi = ei, где 1<=i<=n,
где в качестве неизвестных векторов выступают столбцы искомой матрицы Х, а в качестве известных векторов правой части системы – поочередно столбцы единичной матрицы. Разложение матрицы А достаточно сделать один раз.
Пример 2.3:
Дана матрица А. Найти обратную к ней.
3 2 1
A= 1 1 -1
4 -1 5
Решение:
Приведем аналитическое решение.
Итак, необходимо решить три системы (количество решаемых систем равно порядку исходной матрицы, n=3) любым удобным способом.
1) 3x11+2x21+x31=1 x11+2/3x21+1/3x31=1/3
x11+ x21 – x31=0 ó x11+ x21 - x31=0 ó
4x11 – x21+5x31=0 4x11 - x31 + 5x31=0
x11+2/3x21+1/3x31=1/3 x11+2/3x21+1/3x31=1/3
1/3x21 - 4/3x31=-1/3 ó x21 - 4x31=-1 ó
-11/3x21+11/3x31=-4/3 -11/3x21+11/3x31=-4/3
x11+2/3x21+1/3x31=1/3 x11+2/3x21+1/3x31=1/3 x11=-4/11
x21 - 4x31=-1 ó x21 - 4x31=-1 x21=9/11
-11x31= -5 x31=5/11 x31=5/11
2) 3x12+2x22+x32=0 x12+2/3x22+1/3x32=0
x12+ x22 – x32=1 ó x12+ x22 - x32=1 ó
4x12 – x22+5x32=0 4x12 - x32 + 5x32=0
x12+2/3x22+1/3x32=0 x12+2/3x22+1/3x32=0
1/3x22 - 4/3x32=1 ó x22 - 4x32=3 ó
-11/3x22+11/3x32=0 -11/3x22+11/3x32=0
x12+2/3x22+1/3x32=0 x12+2/3x22+1/3x32=0 x12=1
x22 - 4x32=1 ó x22 - 4x32=3 x22=-1
-11x32= 11 x32=-1 x32=-1
3) 3x13+2x23+x33=0 x13+2/3x23+1/3x33=0
x13+ x23 – x33=0 ó x13+ x23 - x33=0 ó
4x13 – x23+5x33=1 4x13 - x33 + 5x33=1
x13+2/3x23+1/3x33=0 x13+2/3x23+1/3x33=0
1/3x23 - 4/3x33=0 ó x23 - 4x33=0 ó
-11/3x23+11/3x33=1 -11/3x23+11/3x33=1
x13+2/3x23+1/3x33=0 x13+2/3x23+1/3x33=0 x13=3/11
x23 - 4x33=0 ó x23 - 4x33=0 x23=-4/11
-11x33= 1 x33=-1/11 x33=-1/11
Таким образом, обратная матрица к матрице A имеет вид:
-4/11 1 3/11
X= 9/11 -1 -4/11
5/11 -1 -1/11
Проверка: А∙Х = Е
3 2 1 -4/11 1 3/11 1 0 0
1 1 -1 × 9/11 -1 -4/11 = 0 1 0
4 -1 5 5/11 -1 -1/11 0 0 1
В случае составления программы алгоритм следующий:
- Для z от 1 до n выполнить следующее:
- b[z,z]=1
- Для k от 1 до (n-1) выполнить следующее:
- Для i от (k+1) до n выполнить следующее:
-
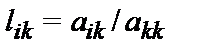
-
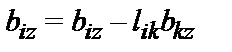
- Для j от (k+1) до n выполнить следующее:
-
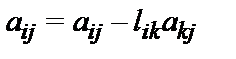
- Для k от n до 1 выполнить следующее:
9. 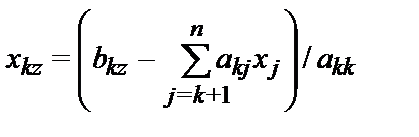
Программа, написанная на языке Pascal , имеет вид:
Uses crt;
Const n1=10;
Var z,k,i,j,n:integer;
l,a,x,b,a1,b1:array[1..n1,1..n1] of real;
sum:real;
BEGIN clrscr;
write('n=');read(n);
For i:=1 to n do
For j:=1 to n do
begin
Write('vvedite a[',i,',',j,']=');
readln(a[i,j]);
end;
Writeln(' matrix À');
For i:=1 to n do
Begin
For j:=1 to n do write(a[i,j],' ');
Writeln;
End;
For z:=1 to n do b[z,z]:=1;
For k:=1 to n-1 do
For i:=k+1 to n do
Begin
l[i,k]:=a[i,k]/a[k,k];
for z:=1 to n do b[i,z]:=b[i,z]-l[i,k]*b[k,z];
For j:=k+1 to n do a[i,j]:=a[i,j]-l[i,k]*a[k,j];
End;
For i:=1 to n do
For j:=1 to n do
Begin
A1[i,j]:=a[i,j]/a[i,i];
for z:=1 to n do B1[i,z]:=b[i,z]/a[I,i];
end;
for z:=1 to n do
For k:=n downto 1 do
begin
For j:=k+1 to n do sum:=sum+a1[k,j]*x[j,z];
x[k,z]:=(b1[k,z]-sum)/a1[k,k]; sum:=0;
end;
writeln;
Writeln('matrix À^(-1)');
For i:=1 to n do
begin
For j:=1 to n do write(x[i,j],' ');
Writeln;
end;
Readln;
END.
По решению СЛАУ
Пусть дана система:
2x + y – z + d = 6
x - 2y + 2z – d = 1
3x + 2y + z – 2d = -2
-x + 3y – 3z + 2d = 1
требуется найти ее решение.
Пакет MathCad дает большие возможности по решению СЛАУ как численно, так и символьно.
Используя матричное исчисление: X= A-1×B.
Вначале задают исходные данные матрицы А и столбца В

Затем вычисляют столбец X (здесь он носит имя x1):

Отметим, что при работе с матрицами в MathCad, ввод матриц ведется с панели инструментов Matrix («Матрица»).
Видно, что значение столбца х1, соответствующее переменой z, равно нулю, но MathCad выводит его в виде числа с плавающей запятой, поэтому иногда применяют преобразование следующего рода:

Но действия по нахождению решения СЛАУ можно реализовывать численно, для этого можно воспользоваться ручным вводом встроенной функцией lsolve (A,B), аргументами которой являются матрица коэффициентов А и свободный столбец В, при этом порядок аргументов имеет значение, так как использование аргументов в обратном порядке не приводит к результатам, а вызывает ошибку вычислений:

Видно, что значение х3 не может быть найдено (при использовании MathCad и переменная А в функции lsolve, и вектор х3 подсвечиваются красным цветом) - это признак методической ошибки.
Если же все записано правильно, то можно найти значения вектора х2:

Отличие значений третьей переменной у непреобразованных векторов х1 и х2 заключается во встроенных методах расчета.
Находить решение, используя обратные матрицы целесообразно, если матрица имеет небольшое число строк и решение должно быть получено однократно, если же матрица громоздка, то решение удобнее искать посредством функции lsolve, в которой заложен метод LU-разложения матрицы.
К матрицам применимы еще несколько удобных встроенных функций MathCad:
детерминант матрицы |A| = -6 
ранг матрицы rank(A) = 4 
сцепление матрицы augment (A,B) работает по правилу объединения вправо:


Очевидно, что и в этой функции порядок введения аргументов важен!
Задания для лабораторной работы №2:
Задание 1.
Найти решение СЛАУ по МГ:
| A | B | ||
| 1 | N | 4 | 2N-3 |
| N-5 | 3 | 2 | N-1 |
| 3 | N-10 | 3 | 2N-20 |
Задание 2.
А) Найти разложение матрицы А на L и U :
| A | ||
| 1 | N | 4 |
| N-5 | 3 | 2 |
| 3 | N-10 | 3 |
Б) Имея две матрицы L и U и столбец В найти: а) матрицу А; б) переменные Y; в) переменные Х:
| 1 | 0 | 0 | 1 | 3 | 4 | |||
| L= | -4 | 15 | 0 | U= | 0 | 1 | 1,2 | |
| 3 | -16 | 10,2 | 0 | 0 | 1 |
| B |
| N-5 |
| -4N-1 |
| 3N-13 |
Задание 3.
Найти обратную матрицу для матрицы А
| A | ||
| 1 | N | 4 |
| N-5 | 3 | 2 |
| 3 | N-10 | 3 |
Задание 4. Найти решение СЛАУ из задания 1 в MathCad путем:
а) использования обратной матрицы;
б) использования функции lsolve.
Контрольные вопросы
1. Какая система уравнений называется системой линейных алгебраических уравнений?
2. В чем заключается методика решения системы методом Гаусса?
3. Как решить систему линейных уравнений по алгоритму метода Гаусса?
4. Какие матрицы получаются при прямом и обратном ходе метода Гаусса?
5. Сколько и каких недостатков у метода Гаусса?
6. Сформулируйте теорему об LU-разложении.
7. Как использовать LU-разложение матрицы при решении системы линейных алгебраических уравнений.
8. Какие произведения матриц L,U будут характеризовать прямой и обратный ход метода Гаусса?
9. Объясните суть использования метода Гаусса при нахождении обратной матрицы.
10. Какие еще существуют методы нахождения обратной матрицы?
Задание 1.
Найти все собственные значения и вектора матрицы А вручную:
6+N 4
A= 8 15-N
Задание 2.
Найти все собственные значения и вектора матрицы А
| A | ||
| 1 | N | 4 |
| N-5 | 3 | 2 |
| 3 | N-10 | 3 |
Посредством использования стандартных функций пакета MathCad.
Контрольные вопросы
1. Какой вектор называется собственным вектором матрицы?
2. Какое число называется собственным значением матрицы?
3. Что такое собственная пара матрицы?
4. Какое уравнение называется вековым?
5. Что такое спектр матрицы?
Метод половинного деления
а=
0
b=
1
ε=
0,01
№ ит
А
c
b
Знак
(f(a))
Знак
(f(c))
Знак
(f(b))
Δ
0
0
0,5
1
-
-
+
1
1
0,5
0,75
1
-
+
+
0,5
2
0,5
0,625
0,75
-
-
+
0,25
3
0,625
0,688
0,75
-
-
+
0,125
4
0,688
0,719
0,75
-
-
+
0,0625
5
0,719
0,734
0,75
-
-
+
0,03125
6
0,734
0,742
0,75
-
+
+
0,015625
7
0,734
0,738
0,742
-
-
+
0,007813
8
0,738
0,740
0,742
-
+
+
0,003906
Как видно из таблицы на 7 -ой итерации получен корень уравнения х=0,738. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой)
Замечание. Для метода половинного деления всегда можно определить количество требуемых итераций по формуле:
n > log2 ((b-a)/e)
где n – ближайшее большее целое число.
Следовательно, для нашей задачи: n > log2 ((1-0)/0.01) = log2100 = 6.64 , то есть n=7, что и видно из таблицы.
Последовательность вложенных сегментов имеет вид:
-[0,1]+ É -[0.5,1]+ É -[0.5,0.75]+ É -[0.625,0.75]+ É -[0.688,0.75]+ É -[0.719,0.75]+ É -[0.734,0.75]+ É -[0.734,0.742]+ É 0.738
Верхние индексы, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала.
Метод итераций.
Метод итераций
а=
0
b=
1
ε=
0,01
№
х
φ(x)
Δ
0
0,5
0,877583
0,5
>
0,01
1
0,877583
0,639012
0,377583
>
0,01
2
0,639012
0,802685
0,23857
>
0,01
3
0,802685
0,694778
0,163673
>
0,01
4
0,694778
0,768196
0,107907
>
0,01
5
0,768196
0,719165
0,073418
>
0,01
6
0,719165
0,752356
0,04903
>
0,01
7
0,752356
0,730081
0,03319
>
0,01
8
0,730081
0,74512
0,022275
>
0,01
9
0,74512
0,735006
0,015039
>
0,01
10
0,735006
0,741827
0,010114
>
0,01
11
0,741827
0,737236
0,00682
<
0,01
12
0,737236
0,74033
0,004591
<
0,01
Как видно из таблицы на 11 -ой итерации получен корень уравнения х=0,742. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой)
Замечание. Для нулевой итерации за х0 взяли среднее значение между a и b, равное 0,5.
Метод хорд. Определим неподвижную точку, для этого проверим условие (4.7) в точках a и b:
f ”(а) × f (а) < 0, f ”( b ) × f ( b ) > 0
Значит, неподвижной точкой является точка b.
Таблица по работе метода хорд имеет вид:
|
Метод хорд | |||||
| а= | 0 | b= | 1 | ε= | 0,01 |
| х_неп=1, f(x_неп)= 0,459698 | х0=0 | ||||
| № | X |
F(x) | Δ | ||
| 0 | 0 | -1 | 1 | > | 0,01 |
| 1 | 0,685 | -0,0893 | 0,685073 | > | 0,01 |
| 2 | 0,736 | -0,00466 | 0,051226 | > | 0,01 |
| 3 |
0,739 | -0,00023 |
0,002646 | < |
0,01 |
| 4 | 0,739 | -1,2E-05 | 0,000133 | < | 0,01 |
Как видно из таблицы на 3 -ей итерации получен корень уравнения x=0,739. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой)
Последовательность вложенных сегментов имеет вид:
-[0,1]+ É -[0.685,1]+ É -[0.736,1]+ É -[0.739,1]+ É 0.739
Верхние индексы, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала.
Метод касательных.
Метод касательных
а=
0
b=
1
ε=
0,01
№
Х
F(x)
F'(x)
Δ
0
0,5
-0,37758
1,479426
1
>
0,01
1
0,755
0,027103
1,685451
0,255222
>
0,01
2
0,739
9,46E-05
1,673654
0,016081
>
0,01
3
0,739
E-09
1,673612
E-05
<
0,01
4
0,739
0
1,673612
7,06E-10
<
0,01
Как видно из таблицы на 3 -ей итерации получен корень уравнения x=0,739. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой)
Последовательность вложенных сегментов имеет вид:
-[0,1]+ É -[0,755]+ É -[0,0.739]+ É -[0,0.739]+ É 0.739.
Верхние индекс, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала.
B(Kасат)
Δ.
0
0
0,5
0,5
>
0,01
1
0,685
0,755
0,070149
>
0,01
2
0,736
0,739
0,002843
>
0,01
3
0,739
0,739
0,00014
<
0,01
4
0,739
0,739
7E-06
<
0,01
Как видно из таблицы на 3 -ей итерации получен корень уравнения, равный x=(a3+b3)/2=0,739. Точность равна 0,01. (для определенности оставим в значении корня третий знак после запятой)
Последовательность вложенных сегментов имеет вид:
-[0,1]+ É -[0.685,0.755]+ É -[0.736,0.739]+ É -[0.739,0.739]+ É 0.739.
Верхние индексы, стоящие слева и справа от отрезка, показывают знак функции соответственно в левом и правом конце интервала.
По поиску корней уравнения
MathCad позволяет находить корни любого уравнения с одним неизвестным f(x) = 0 в численном виде, а для многих уравнений и в аналитическом (символьном виде). Если уравнение можно решить аналитически, то приводятся сразу все корни (исключая тригонометрические уравнения, где приводится один корень). Если же уравнение решается численно, то целесообразно вначале локализовать корень, то есть выделить отрезок существования лишь одного пересечения графика функции y = f(x) с осью абсцисс.
Для решения уравнения в аналитическом виде используется оператор solve, вызываемый с панели инструментов Solving(«Символика»), при этом уравнение в левой части оператора solve необходимо вводить в виде f(x)=0, где знак «=» вводится с панели булевых операторов.
Пример 4.2.
Найти решение уравнения из примера 4.1.
Решение.

Как видно, решение уравнения совпадает с ранее найденным различными численными методами. Тот же ответ дает использование оператора root :

Приведенное решение показывает, что вначале необходимо ввести начальное приближение к корню, если же необходимо найти корень на отрезке , то функция root может быть записана иначе:

Получаемый ответ тот же.
Помимо root, для f(x), имеющих вид полинома, можно использовать функцию polyroots, которая позволяет найти все корни уравнения f(x)=0, включая комплексные, но в качестве аргумента используется не функция f(x), а вектор коэффициентов полинома, начиная со свободного.
Пример 4.3.
Для функции f(x) = x2 - 10x + 13 найти корни.
Решение.
Функция является левой частью уравнения (1) для матрицы из примера 3.2:

Полученное решение совпадает с уже найденным.
Задания для лабораторной работы №4:
Задание 1.
а) Известно, что вещество С расходуется в мономолекулярной реакции с константой скорости k=8,2*10-2 с-1. Начальное значение концентрации вещества С равно N*10-2. Определить аналитическую зависимость для концентрации вещества С от времени реакции и найти такое время, при котором значение концентрации вещества С было бы равно N*10-3.
Примечание. Для решения задачи принять: а=25 с, b=35 c, e=0,001.
б) Найти решение скалярного уравнения: y = sin(N) + lg(x) + x – 10,5, a=8, b=12, e=0.001.
Задание 2.
а) - Построить в редакторе EXCEL (GNUPLOT) графическую зависимость C(t), ограничив время реакции 45 сек.
- Табулирование функции вести с шагом по t, равным 3 с.
- Шкала графика по оси C имеет:
максимальное значение = 3/2* N*10-2;
минимальное значение = -3/2* N*10-2
цена основного деления = 5* N*10-3.
б) Построить в редакторе GNUPLOT график функции y(x) на промежутке [a,b] с шагом по сетке, равным (b-a)/10. Добавить на рисунок надпись «Точка пересечения графика функции y(x)=… с осью Ох есть точка х=…».
Задание 3.
Найти решение задач в MathCad:
а) из задания 1 а) путем использования функции root с локализацией и без локализации корня, приняв за начальное приближение t=0;
б) из задания 1 б) путем использования функции root с локализацией и без локализации корня, приняв за начальное приближение х=25;
в) в обоих случаях построить графики функций на соответствующих отрезках: a) [0;45]; б) [25;35].
Контрольные вопросы
1. Сформулируйте теорему о существовании нуля непрерывной функции.
2. Какие случаи поведения функции возможны на выбранном отрезке.
3. Назовите суть метода бисекции.
4. Как рассчитать количество итераций при поиске корня заданного уравнения, используя метод бисекции?
5. Назовите суть метода итераций.
6. Для каких функций подходит метод итераций при поиске нуля функции?
7. Какая формула применяется для остановки работы алгоритма метода итераций?
8. Назовите суть метода хорд.
9. Назовите суть метода касательных.
10. В чем преимущество комбинированного метода хорд и касательных?
ТЕМА 5. ПРИБЛИЖЕНИЕ ФУНКЦИЙ
На отрезке [a,b] рассматривается функция y=f(x), значения которой определены лишь в конечном числе точек. Эти точки образуют на отрезке [a,b] сетку
a=x0<x1<x2<…<xn-1<xn=b (5.1)
а соответствующие им значения функции f:
yi = f ( xi ), i=0, 1, 2, …, n (5.2)
представляют собой сеточную функцию. Такой способ задания функции называется табличным.
Задача аппроксимации заключается в следующем: по сеточной функции (5.1),(5.2) построить функцию непрерывного аргумента g ( x ), аппроксимирующую функцию f ( x ): g ( x ) » f ( x ).
Это позволит приближенно вычислять функцию f ( x ) в любой точке отрезка [ a , b ], а не только в точках сетки (5.1).
Интерполирование.
Пусть дана система функций j 0 ( x ), j 1 ( x ), …, j n ( x ), определенная на отрезке [a,b]. Для этой системы ищется аппроксимирующая функция g ( x ) в виде линейной комбинации функций:
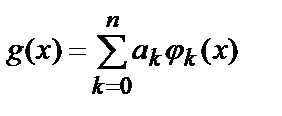 (5.3)
(5.3)
Требование: в точках сетки (5.1) функция g (х) должна принимать такие же значения (5.2), что и функция f ( x ):
g ( xi )= f ( xi ) (5.4)
Сформулированную таким образом задачу построения функции непрерывного аргумента g ( x ), аппроксимирующей функцию f ( x ), называют задачей интерполирования.
Наиболее часто рассматривают интерполирование полиномами, тогда:
j 0 ( x )=1, j 1 ( x )= x , …, j n ( x )= xn . (5.5)
В этом случае функция g ( x ) записывается как полином n-ой степени:
g(x)=Pn(x)=a0+a1x+a2x2+…+anxn. (5.6)
Существует несколько форм его записи, одна из них принадлежит Лагранжу:
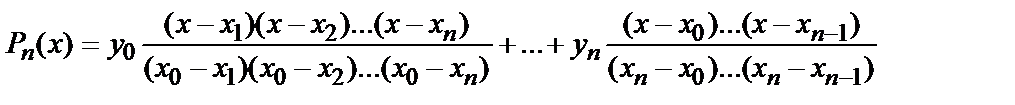 (5.7)
(5.7)
При этом условие (4.6) выполняется во всех точках сетки:
Pn ( xi )= yi , i =0, 1, 2,…, n (5.8)
Пример 5.1. Построить интерполяционный полином для функции y=sin(x). Сетка состоит из трех точек: x0 = 0, x1 = π/6, x2 = π/2. Сеточная функция имеет вид: y0 = 0, y1 = 1/2, y2 = 1.
Решение:
Поскольку максимальный индекс точек сетки равен 2, то и степень интерполяционного полинома будет равна двум. Используя формулу Лагранжа (4.7), получится:
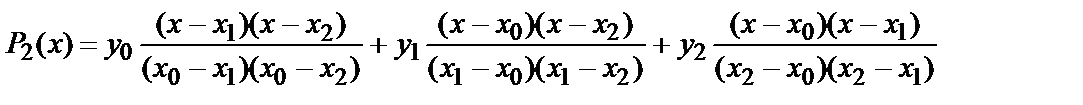
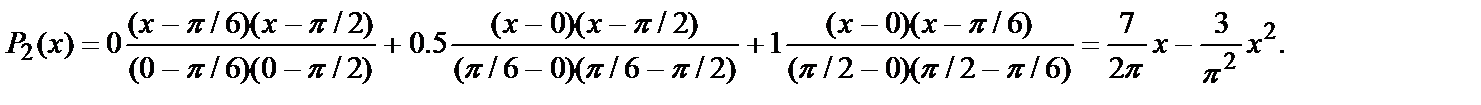
Легко проверить, что в точках сетки этот полином Р2(х) принимает нужные значения.
Для определения погрешности интерполирования можно рассчитать значение sin(x) и P2(x) в точке х= π/4:
e=sin(π/4) – P2(π/4) = 0.7071 – 0.6875 = 0.02
Значительная величина погрешности определяется тем, что на отрезке длиной π/2, взята грубая сетка, состоящая всего из трех точек.
Метод наименьших квадратов.
А) аппроксимация полиномами.
В методе наименьших квадратов аппроксимирующая функция y(x) ищется в виде суммы, аналогичной (5.3), но содержащей сравнительно небольшое число слагаемых:
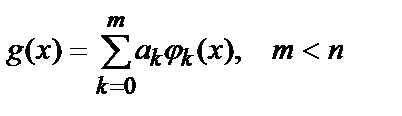 (5.9)
(5.9)
Предполагая, что каким-то образом выбраны коэффициенты ak, тогда в каждой точке сетки (451) можно вычислить погрешность:
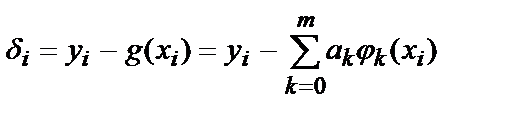 (5.10)
(5.10)
Функция δ, принимающая значения δ1, δ2, …, δn, представляет собой сеточную функцию и называется погрешностью решения .
Сумма квадратов этих величин называется суммарной квадратичной погрешностью:
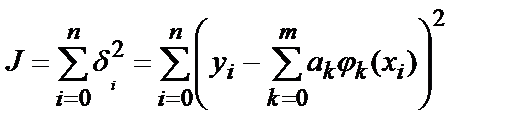 (5.11)
(5.11)
Возникает задача: найти такой набор коэффициентов ak , при которых суммарная квадратичная погрешность J оказывается минимальной.
Функцию (5.9) с набором коэффициентов, удовлетворяющих этому требованию, называют наилучшим приближением по наименьших квадратов.
Построение наилучшего приближения сводится к задаче поиска экстремума функции J от нескольких переменных:
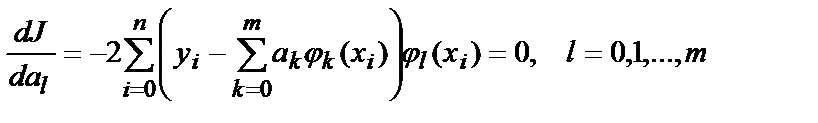 (5.12)
(5.12)
Уравнения (4.12) можно переписать в виде:
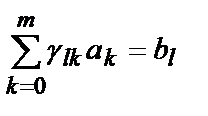 , l=0,1,…,m (5.13)
, l=0,1,…,m (5.13)
где
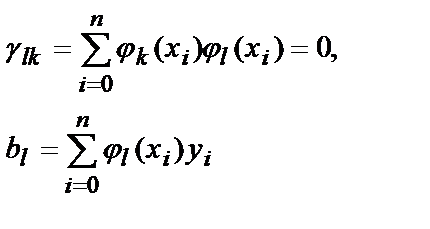 (5.14)
(5.14)
Таким образом, получена система линейных алгебраических уравнений (5.14), в которой роль неизвестных играют искомые коэффициенты разложения a0, a1, … , am.
Пример 5.2. Пусть известны экспериментальные значения концентрации некоторого вещества M в зависимости от времени протекания реакции:
Таблица 1.
| t, min | M, моль/л |
| 30 | 1,526 |
| 40 | 1,341 |
| 50 | 1,195 |
| 60 | 0,962 |
| 70 | 0,871 |
Считая, что концентрация вещества описывается полиномом второй степени, определить его коэффициенты.
Решение:
Здесь общее количество точек равно 5, степень полинома m =2, j 0 (х)=1, j 1 (х)=х, j 2 (х)=х2.
Для нахождения коэффициентов полинома, необходимо решить систему линейных уравнений. Определим ее коэффициенты:
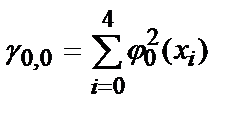 ,
, 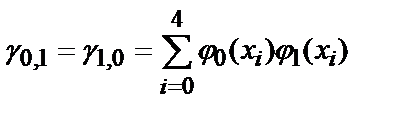 ,
, 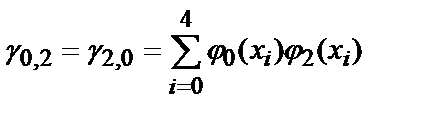
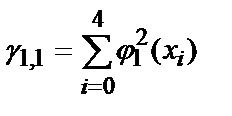 ,
, 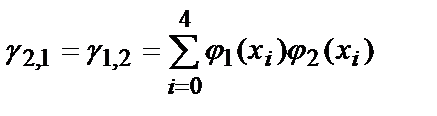 ,
, 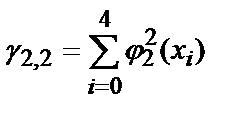
g 0,0 =5, g 0,1 =250, g 0,2 =13 ¢ 500, g 1,1 =13 ¢ 500, g 1,2 =775 ¢ 000, g 2,2 =46 ¢ 590 ¢ 000
и коэффициенты, стоящие в правых частях системы:
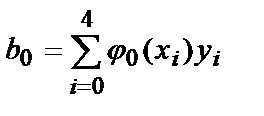 ,
, 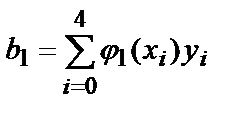 ,
, 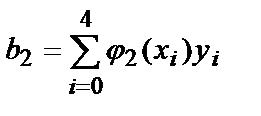
b 0 = 5,895 , b 1 =27 7,86 , b 2 =1423 7,6
Итоговая система для определения коэффициентов имеет вид:
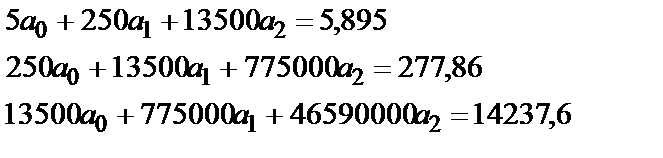
Для решения этой системы можно использовать любые имеющиеся пакеты математических прикладных программ, в том числе можно использовать и написанную программу для решения систем линейных алгебраических уравнений, приведенной в теме 2.
Применяя эту программу, можно рассчитать коэффициенты а0, а1, а2.
Окно ввода этой программы будет иметь вид:
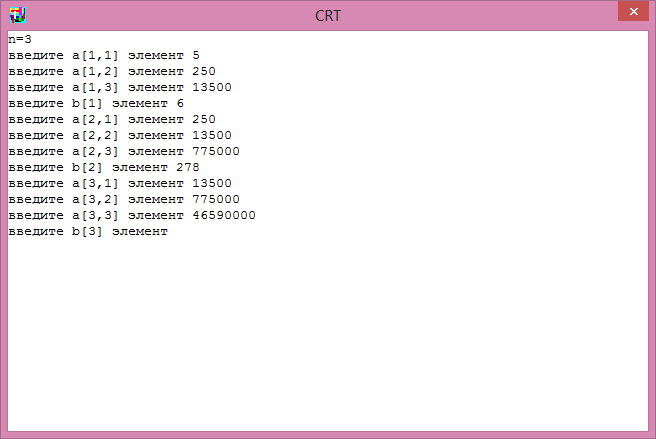
Данные в программу вводятся согласно вышеописанной системе.
После введения данных программа выдает исходную матрицу А и после этого преобразованную матрицу. Поскольку матрица верхнетреугольная, то при выводе второй и третьей строк они немного смещены влево относительно первой строки. В правой части каждой строки стоят значения bi.
Значения полученных переменных даны в виде x[1], x[2], x[3].
Следует учитывать, что коэффициент x[1] – это коэффициент, стоящий при х2, т.е. а2 ; коэффициент х[2] это коэффициент, стоящий при х, т.е. а1; а x[3] – это коэффициент, стоящий без х, т.е. а0..
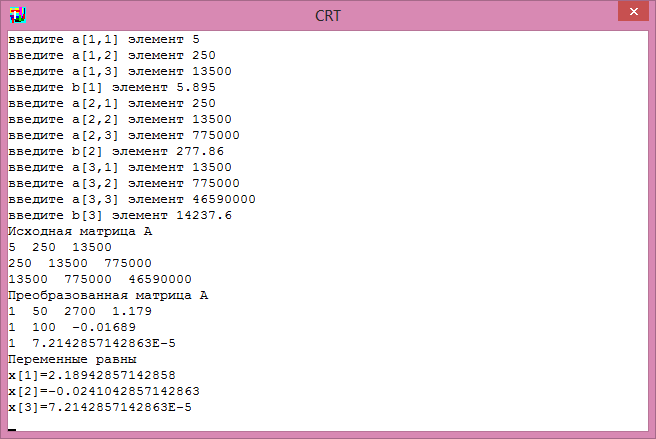
Зная эти значения, можно выписать уравнение квадратичной функции, аппроксимирующей экспериментальные данные:
Р2(х) = 7 × 10-5 x2 - 0,024 x + 2,19 (5.15)
Экспериментальные и расчетные значения показаны в таблице:
| t, min | M, моль/л | P2 |
| 30 | 1,526 | 1,531229 |
| 40 | 1,341 | 1,340686 |
| 50 | 1,195 | 1,164571 |
| 60 | 0,962 | 1,002886 |
| 70 | 0,871 | 0,855629 |
Рассчитаем суммарную квадратичную погрешность замены экспериментальных значений функцией вида (4.15):
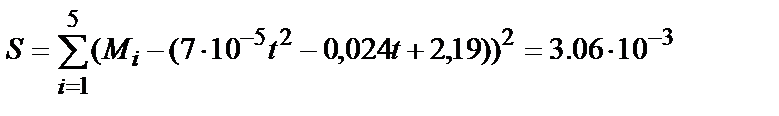
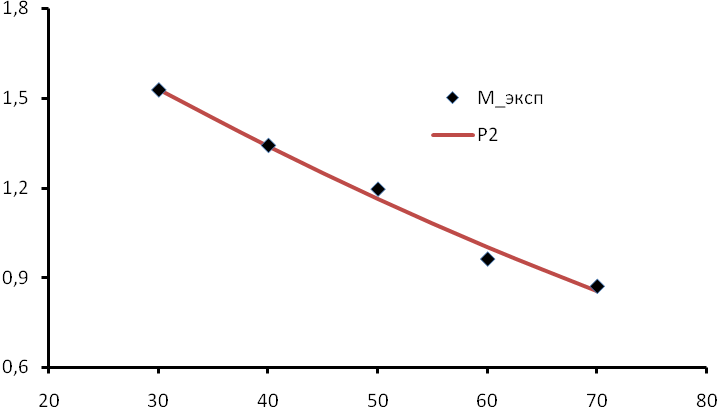
Таким образом, найденная зависимость, описываемая уравнением (5.15), имеет достаточно хорошую согласованность с эмпирически полученными значениями М., что видно по следующему рисунку:
Б) аппроксимация методом выравнивания (линеаризация).
Очень часто вид эмпирической зависимости подсказывает исследователю, какой именно аналитической функцией ее можно описать. Но, зачастую, количество параметров, от которых зависит выбранная аналитическая функция больше двух. Для их определения необходимо применять методы оптимизации, которые дадут значения параметров с некоторой погрешностью.
Однако, если выбранная аналитическая зависимость характеризуется лишь двумя параметрами, то можно использования метод выравнивания. Лишь после этого можно перейти к отысканию тех значений постоянных коэффициентов, которые дадут наилучшее приближение экспериментальных и расчетных величин.
Метод выравнивания заключается в преобразовании функции y=j(x) таким образом, чтобы превратить ее в линейную функцию. Достигается это путем замены переменных х и y новыми переменными:
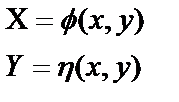 (5.16)
(5.16)
которые выбираются так, чтобы получилось уравнение прямой:
Y = A + BX (5.17)
Числовые значения коэффициентов А и В определяются как:
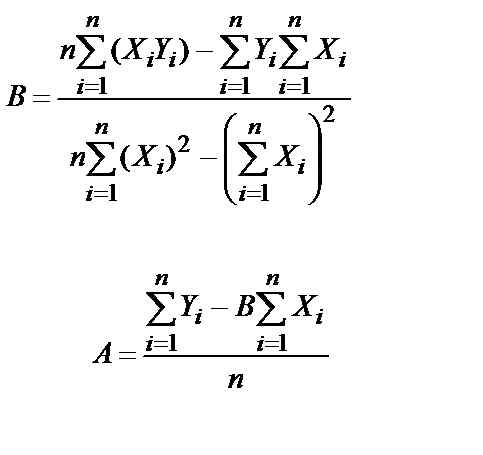 (5.18)
(5.18)
Пример 5.3. Изменение концентрации вещества M в реакции подчиняется экспоненциальному закону 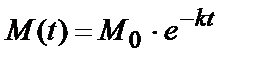 . Необходимо определить начальное значение вещества M 0 и значение константы скорости расхода вещества k .
. Необходимо определить начальное значение вещества M 0 и значение константы скорости расхода вещества k .
Решение:
Для того, чтобы превратить исходную экспоненциальную зависимость в линейную, необходимо ее прологарифмировать. Тогда получим:
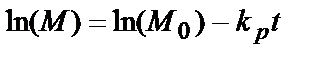 (5.19)
(5.19)
Вводя новые переменные: Y = ln ( M ), A = ln ( M 0 ), B = –- kP, X = t
cоставим дополнительную таблицу (помимо таблицы 1) для расчета коэффициентов линейной зависимости Y(X):
Таблица 2.
| X | Y | XY | X2 |
| 30 | 0.423 | 12.678 | 900 |
| 40 | 0.293 | 11.736 | 1600 |
| 50 | 0.178 | 8.905 | 2500 |
| 60 | -0.039 | -2.322 | 3600 |
| 70 | -0.138 | -9.667 | 4900 |
| 250 | 0.717 | 21.330 | 13500 |
В последней строке таблицы приведены суммы величин.
Подставляя требуемые значения в формулу (4.18), рассчитаем коэффициенты линейной зависимости:
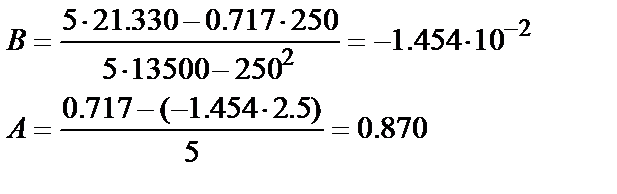
Отсюда, kP =1.45 × 10-2, М0 = е0.87 = 2.39.
Следовательно, экспоненциальное уравнение, описывающее изменение концентрации вещества M в реакции имеет вид:
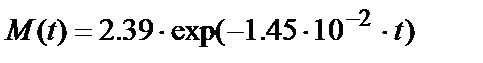 (5.20)
(5.20)
Таблица данных, содержащая экспериментальные значения М и расчетную зависимость приведена ниже:
| t, min | M_расч | М_расч |
| 30 | 1,526 | 1,546963 |
| 40 | 1,341 | 1,338157 |
| 50 | 1,195 | 1,157536 |
| 60 | 0,962 | 1,001294 |
| 70 | 0,871 | 0,866142 |
Таблица проиллюстрирована на следующем рисунке:
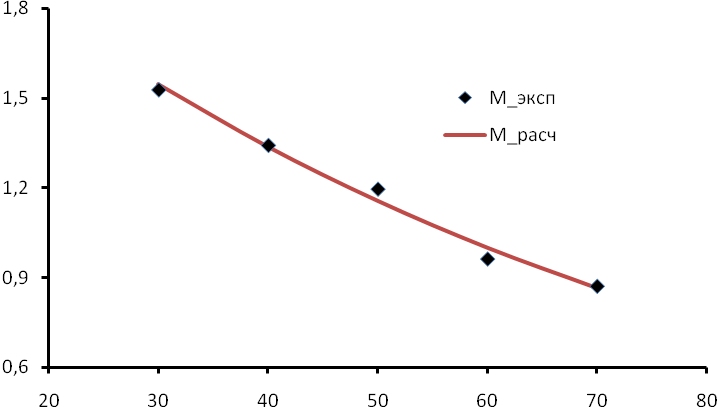
Рассчитаем суммарную квадратичную погрешность замены экспериментальных значений функцией вида (5.20):
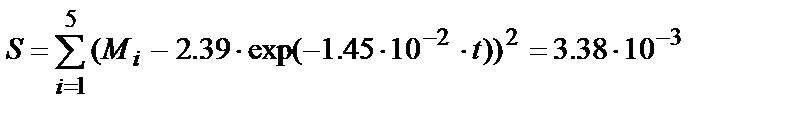
Таким образом, найденная зависимость, описываемая уравнением (5.20), имеет также достаточно хорошую согласованность с эмпирически полученными значениями М.
В) Сравнение методов
Проанализируем полученные в пунктах А) и Б) значения. Для этого достаточно сравнить эти значения между собой.
Сравнение можно провести путем поиска наименьшего среди суммарных отклонений функции.
В данном случае наилучшее приближение дает описание экспериментальной кривой полиномом второго порядка. Квадратичная погрешность замены экспериментальных значений функциональной зависимостью равна:
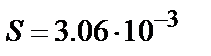
Это означает, что полином второго порядка лучше приближен к экспериментальным точкам, чем экспоненциальная зависимость. Хотя, экспоненциальная зависимость дает возможность определять недостающие кинетические параметры: начальную концентрацию и константу скорости реакции.
Поэтому, при решении задачи аппроксимации выбор аппроксимирующей функции следует делать, исходя из требований и условий задачи.
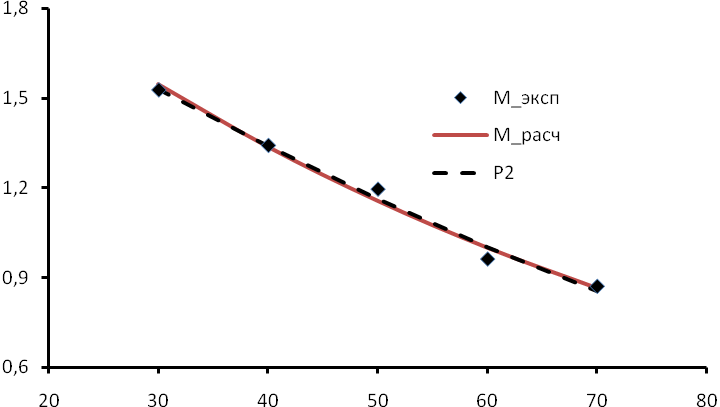
Как видно по рисунку, сравнение «на глаз» невозможно, поскольку графики расчетных зависимотей сливаются между собой, поэтому единственно допустимым способом выбора вида аппроксимирующей функции остается поиск наименьшей суммарной квадратичной погрешности.
Вообще говоря, некоторые пакеты прикладных программ имеют в своем арсенале готовые модули, позволяющие подбирать для экспериментальной зависимости аналитические функции различного вида.
Выбор той или иной аппроксимирующей функции пользователь делает сам, а на экран выдается коэффициент корреляции.
По аппроксимации функций
Пакет MathCad предоставляет пользователю достаточно большие возможности по аппроксимации различных функций, однако здесь мы приведем лишь некоторые из них – это поиск линейной и полиномиальной зависимостей.
Пример 5.4.
Пусть даны значения х и y:
| X | Y |
| 30 | 0.423 |
| 40 | 0.293 |
| 50 | 0.178 |
| 60 | -0.039 |
| 70 | -0.138 |
Решение. Используя функцию line, можно получить значения коэффициентов А и В:






Тогда можно построить два графика h(t) и M(t) в одной плоскости, здесь за M(t) считается M1Т:

Если считать, что найденные значения А и В можно перевести в kр и М0, то kP=1.45×10-2, М0 = е0.87 = 2.39.
Пример 5.5.
Даны значения
| t, min | M_расч |
| 30 | 1,526 |
| 40 | 1,341 |
| 50 | 1,195 |
| 60 | 0,962 |
| 70 | 0,871 |
Описать эту зависимость полиномом второго порядка
Решение.
Необходимо ввести три вектора

 ,
,
где vs – вектор весовых коэффициентов каждой точки матрицы М, поскольку все точки равнозначны, то их весовые коэффициенты можно задать единичными.
В столбец К вводят функции, являющиеся jk(x) из уравнения (5.9), для полинома второй степени их ровно три:


Переменная s и будет рассчитывать коэффициенты Р2(х).

Тогда l(t) будет реализовывать значения полинома второго порядка.

По рисунку видно, что расчетный полином второго порядка l(t) хорошо аппроксимирует экспериментальные данные. Сопоставляя два последних рисунка можно сделать вывод, что и экспоненциальная, и квадратичная зависимости удовлетворительно описывают экспериментальные данные. Следовательно, провести выбор более «лучшей» аппроксимирующей кривой можно лишь на основании дополнительно проведенных исследований.
Задания для лабораторной работы №5
Задание 1.
А) Экспериментальные зависимости теплоемкости некоторого вещества от температуры представлены в виде таблицы:
| Т, Со | Ср (Дж/(моль×К) |
| N | 1.0029 |
| N+5 | 1.0013 |
| N+10 | 1.0000 |
| N+15 | 0.9990 |
| N+20 | 0.9983 |
описать эту зависимость интерполяционным многочленом.
Б) Построить в табличном редакторе Excel (Gnuplot) графические зависимости для экспериментальных данных (точки) и расчетных данных (сплошная линия).
Задание 2.
А) Экспериментальные данные по скорости реакции W в зависимости от концентрации С представлены в таблице:
| С*104 М | W |
| (N+1) | 0.042 |
| (N+1)*2 | 0.112 |
| (N+1)*3 | 0.182 |
| (N+1)*4 | 0.246 |
| (N+1)*5 | 0.262 |
Описать эту зависимость многочленом 2 порядка.
Б) Построить в табличном редакторе Excel (Gnuplot) графические зависимости для экспериментальных данных (точки) и расчетных данных (сплошная линия).
Задание 3.
А) Скорость реакции n-ого порядка описывается следующим уравнением 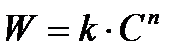 .
.
Экспериментальные данные представлены в таблице:
| C×104 моль/л | W |
| (N+1) | 0.042 |
| (N+1)*2 | 0.112 |
| (N+1)*3 | 0.182 |
| (N+1)*4 | 0.246 |
| (N+1)*5 | 0.262 |
Определить порядок реакции n и константы скорости k методом выравнивания, рассчитав коэффициенты линейной функции, описывающей эти данные.
Б) Построить в табличном редакторе Excel (Gnuplot) графические зависимости для экспериментальных данных (точки) и расчетных данных (сплошная линия).
Задание 4.
Применяя пакет MathCad, сделать следующее:
а) Для таблицы данных:
| Т, Со | Ср (Дж/(моль×К) |
| N | 1.0029 |
| N+5 | 1.0013 |
| N+10 | 1.0000 |
| N+15 | 0.9990 |
| N+20 | 0.9983 |
описать зависимость интерполяционным многочленом 4-го порядка.
б) Для таблицы данных
| С*104 М | W |
| (N+1) | 0.042 |
| (N+1)*2 | 0.112 |
| (N+1)*3 | 0.182 |
| (N+1)*4 | 0.246 |
| (N+1)*5 | 0.262 |
подобрать линейную зависимость.
Контрольные вопросы
1. Как ставится задача аппроксимации?
2. Какая функция называется сеточной?
3. Что такое интерполяция?
4. Какой многочлен называется интерполяционным?
5. Выпишите формулу интерполяционного многочлена Лагранжа?
6. В чем его преимущества и недостатки?
7. В чем заключается метод наименьших квадратов?
8. Какова максимальная и минимальная степени интерполяционного полинома?
9. Как вычислить суммарную квадратичную погрешность?
10. На чем основан выбор аппроксимирующей функции?
DC/dt
C (t)
0
-0,00082
| Расчетная формула в ячейке C3: =C2+1*B2 |
1
-0,00075
0,00918
2
-0,00069
0,008427
3
-0,00063
0,007736
Составим таблицу расчетов по методу Эйлера с шагом t=0,5:
| T |
DC/dt |
C (t) |
| 0 | -0,00082 | 0,01 |
| 0,5 | -0,00079 | 0,00959 |
| 1 | -0,00075 | 0,009197 |
| 1,5 | -0,00072 | 0,00882 |
| 2 | -0,00069 | 0,008458 |
| 2,5 | -0,00067 | 0,008111 |
| 3 | -0,00064 | 0,007779 |
в) Построим графики по полученным таблицам в одной координатной плоскости.
По рис.2 видно, что численные решения, полученные методом Эйлера с шагом 1 и 0,5, хорошо согласуются между собой. Это говорит о гладкости функции C(t).
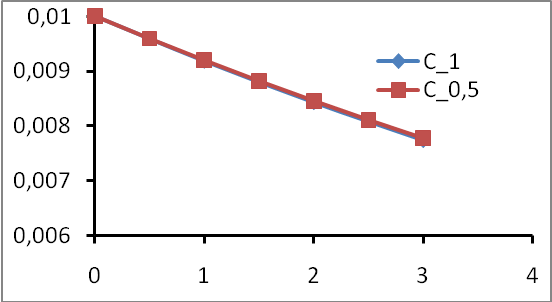
г) По полученным таблицам достаточно легко определить погрешность решения и погрешность аппроксимации при замене функции C(t) численными решениями.
Для нахождения Z сравним значения столбцов C в обоих случаях, а для нахождения y – значения столбцов dC/dt. Поскольку, максимальный шаг по t равен 1, то и сравниваемые значения будут располагаться в точках с шагом 1:
| t | Z=|C_1-C_0.5| | T | |С'_1-C'_0.5| | |
| 0 | 0 | 0 | 0 | |
| 1 | 1,681E-05 | 1 | 1,37842E-06 | |
| 2 | 3,08914E-05 | 2 | 2,5331E-06 | |
| 3 | 4,25764E-05 | 3 | 3,49127E-06 | |
| max= |
E-05 | max= |
E-06 |
Найденные значения максимумов и дадут значения погрешностей решения и аппроксимации функции.
Задание 1.
Выписать систему дифференциальных уравнений, каждое из которых представляет собой скорость изменения концентрации отдельного вещества в течение процесса.
Задание 2.
Найти решение системы методом Эйлера на отрезке по времени [0,2]:
А) с шагом 0,5;
Б) с шагом 0,25.
Задание 3.
Найти решение системы методом Рунге-Кутта 4-ого порядка на отрезке по времени [0,2] с шагом 0,5.
Определить величину погрешности и аппроксимации для функции A(t), принимая за аналитическое решение – решение, полученное методом Рунге-Кутта, а за численное решение – решение, полученное методом Эйлера.
Задание 4.
Построить в одной координатной плоскости два графика для функции А(t): решение системы ДУ методом Эйлера и методом Рунге-Кутта.
Задание 5 .
Построить в пакете MathCad таблицу, представляющую решение системы дифференциальных уравнений, описывающих химический процесс. Использовать методы rkfixed и Rkadapt.
Задание 6.
Создать графики функций А и С в одной координатной плоскости, в качестве основы принять таблицу, построенную методом rkfixed.
Задание 7.
Подготовить печатный экземпляр работы с выполненными заданиями.
Контрольные вопросы
1. Какая задача называется задачей Коши?
2. Соблюдение каких условий требуется для решения задачи Коши?
3. Опишите суть метода ломаных Эйлера.
4. Что такое точность метода?
5. Дайте определение разностной схемы метода.
6. Что такое порядок метода?
7. Что такое точность метода?
8. Дайте определение погрешности аппроксимации и погрешности решения.
9.. В чем недостаток и преимущество метода Эйлера?
10. Каков порядок метода Рунге-Кутты?
Формула прямоугольников.
Пусть отрезок [a,b] разбит на n равных частей длины h=(b-a)/n, и в качестве точек ξk выбраны средние точки соответствующих отрезков: ξ k = a + h ( k – 1/2) ( k =1,2,…, n ). В этом случае выражение для интегральной суммы примет вид:
In = ( f (ξ1) + f (ξ2) + … + f (ξ n ))( b - a )/ n (7.1)
Если функция f(x) интегрируема на отрезке [a,b], то
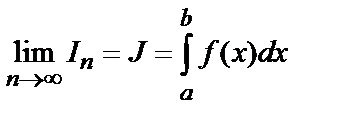 (7.2)
(7.2)
Согласно этой формуле выражение для интеграла J можно записать в виде J=In + αn, причем 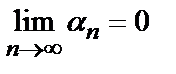 =0. Пренебрегая величиной an , получают приближенную формулу для вычисления интеграла J, которую и называют формулой прямоугольников:
=0. Пренебрегая величиной an , получают приближенную формулу для вычисления интеграла J, которую и называют формулой прямоугольников:
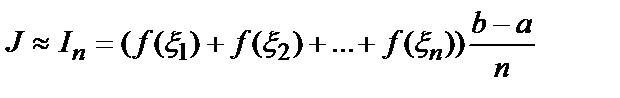 (7.3)
(7.3)
Таким образом, интеграл J – это площадь фигуры криволинейной трапеции, а интегральная сумма, которой приближенно аппроксимируется интеграл, – площадь фигуры, составленной из прямоугольников.
| y=f(x) |
| y |
| O |
| a |
| b |
| x |
.
Вид ступенчатой фигуры показан на рисунке.
Формула трапеций.
Предположим, что отрезок [a,b] разбит на n равных частей длины h=(b-a)/n точками xk=a+kh (k=0,1,2,…,n, x0=a, xn=b). При этом, на каждом из отрезков [xk-1, xk] определим линейную функцию такую, что в граничных точках она принимает те же значения, что и функция f(x). Обобщая эту линейную функцию на n отрезков, можно выписать линейную функцию gn(x):
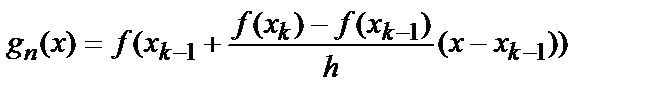 ) (7.4)
) (7.4)
x Î [ xk -1 , xk ], k =1,2,…, n
Ее график представляет собой ломаную линию, начальная, конечная и угловые точки которой принадлежат также графику функции f(x).
| y=f(x) |
| y |
| O |
| a |
| b |
| x |
С увеличением n число общих точек графика растет и ломаная y=gn(x) приближается к линии y=f(x).
Интеграл равен площади фигуры, ограниченной графиком функции gn(x), осью х и вертикальными линиями x=xk-1, x=xk. В этом случае фигура является трапецией и, соответственно, полученная формула показывает площадь этой трапеции.
Переходя ко всему отрезку [a,b]:
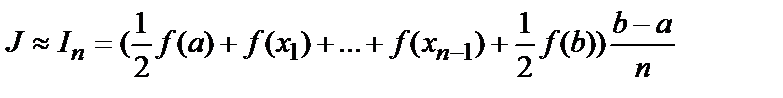 (7.5)
(7.5)
Формула трапеций имеет второй порядок точности.
Формула Симпсона.
Идея замены графика функции f(x) на отрезке [xk-1, xk] линейной функций была использована Симпсоном, который предложил в качестве функции gn(x) использовать полином второго порядка. Тогда интеграл J будет равен:
J » In=(f(a)+4f(x1)+2f(x2)+…+2f(xn-2)+4f(xn-1)+f(b))(b-a)/(3n)
Единственное условие для возможности применения формулы Симпсона для приближенного расчета интеграла – это четное число отрезков разбиения, то есть n-четно.
| y=f(x) |
| y |
| O |
| a |
| b |
| x |
На данном рисунке количество частей разбиении исходного отрезка равно четырем – четное число.
Поскольку аппроксимирующая функция более гладкая по сравнению с другими, то порядок формулы равен 4-м.
Пример 7.1.
Найти интеграл 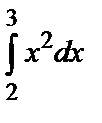 по формулам при n=10:
по формулам при n=10:
а) Ньютона-Лейбница; б) прямоугольников; в) трапеций; г) Симпсона.
Решение.
Приведем графическую интерпретацию поставленной задачи.
| y=x2 |
| y |
| O |
| 1 |
| 2 |
| x |
| 2 |
Требуется найти площадь фигуры, ограниченной слева прямой х=2, справа – прямой х=3, снизу – осью абсцисс, а сверху – графиком функции y=x2.
А) Используя формулу Ньютона-Лейбница, получается:
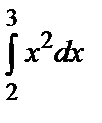 =33/3 – 23/3 = 19/3 = 6,3333
=33/3 – 23/3 = 19/3 = 6,3333
Б) Для наглядности решение поставленной задачи по формуле прямоугольников приведем в виде таблицы:
| X | K | Ξk | f(ξk) |
| 2 | 0 |
|
|
| 2,1 | 1 | 2,05 | 4,2025 |
| 2,2 | 2 | 2,15 | 4,6225 |
| 2,3 | 3 | 2,25 | 5,0625 |
| 2,4 | 4 | 2,35 | 5,5225 |
| 2,5 | 5 | 2,45 | 6,0025 |
| 2,6 | 6 | 2,55 | 6,5025 |
| 2,7 | 7 | 2,65 | 7,0225 |
| 2,8 | 8 | 2,75 | 7,5625 |
| 2,9 | 9 | 2,85 | 8,1225 |
| 3 | 10 | 2,95 | 8,7025 |
| S= |
63,325
h=(3-2)/10=
0,1
I=h*S=
6,3325
Ошибка расчета составит: Er=|6,3333-6,3325|=0,0005.
В) Аналогично представим расчет по формуле трапеций в виде таблицы:
| X | K | f(x) |
| 2 | 0 | 4 |
| 2,1 | 1 | 4,41 |
| 2,2 | 2 | 4,84 |
| 2,3 | 3 | 5,29 |
| 2,4 | 4 | 5,76 |
| 2,5 | 5 | 6,25 |
| 2,6 | 6 | 6,76 |
| 2,7 | 7 | 7,29 |
| 2,8 | 8 | 7,84 |
| 2,9 | 9 | 8,41 |
| 3 | 10 | 9 |
| h=0,1 | I= |
6,335 |
Ошибка расчета составит: Er=|6,3333-6,3350|=0,0020.
Г) Таблица для формулы Симпсона:
| X | K | f(x) |
| 2 | 0 | 4 |
| 2,1 | 1 | 4,41 |
| 2,2 | 2 | 4,84 |
| 2,3 | 3 | 5,29 |
| 2,4 | 4 | 5,76 |
| 2,5 | 5 | 6,25 |
| 2,6 | 6 | 6,76 |
| 2,7 | 7 | 7,29 |
| 2,8 | 8 | 7,84 |
| 2,9 | 9 | 8,41 |
| 3 | 10 | 9 |
| h=0,1 | I= |
6,33333 |
Ошибка расчета составит: Er=|6,3333-6,3333|=0,0000.
Как видно из приведенного примера, наилучшее приближение к значению интеграла, найденного по формуле Ньютона-Лейбница, имеет формула Симпсона.
Задание для лабораторной работы №7.
Известно, что некоторое вещество образуется в реакции со скоростью, описываемой функцией W=Net+5. Определить количество образованного вещества за время [N/10,(N+1)/10], используя для расчета при n=20:
а) формулу Ньютона-Лейбница;
б) формулу прямоугольников;
в) формулу трапеций;
г) формулу Симпсона;
д) провести сравнительный анализ ошибки вычисления
е) пакет MathCad, определяя численное значение интеграла посредством Solve и строя график функции;
ж) пакет MathCad, определяя численное значение интеграла посредством введения вычислительного блока.
Контрольные вопросы
1. Чем заменяется интеграл при использовании любой численной формулы?
2. Какая формула используется в методе прямоугольников?
3. Как будет выглядеть графически метод прямоугольников?
4. Какая формула используется в методе трапеций?
5. Как будет выглядеть графически метод трапеций?
6. Какая формула используется в методе Симпсона?
7. Как будет выглядеть графически метод Симпсона?
8. Каков порядок метода трапеций?
9. Какой порядок метода Симпсона?
10. Укажите, в чем различие между этими тремя формулами?
Тестовые вопросы
Вопрос 1.
Как наглядно представлена матрица размером 3х3:
1.Таблица, имеющая 2 строки и 3 столбца
2.Таблица, имеющая 3 строки и 3 столбца
3.Таблица, имеющая 3 строки и 2 столбца
4.Таблица, имеющая 2 строки и 2 столбца
Вопрос 2.
Обратная матрица существует лишь для …
1. Невырожденных матриц
2. Вырожденных матриц
3. Собственных матриц
4. Несобственных матриц
Вопрос 3.
Какой вид решения системы линейных алгебраических уравнений не существует?
1. Метод Гаусса
2. Метод Крамера
3. Метод Кантора
4. Метод линейных преобразований
Вопрос 4.
Приведение матрицы к ступенчатому виду – это суть …
1. Метод Гаусса
2. Метод Крамера
3. Метод Кантора
Вопрос 5.
Существование решение СЛАУ – это вопрос о …
1. Обычности СЛАУ
2. Совместности СЛАУ
3. Общности СЛАУ
4. Конечности СЛАУ
Вопрос 6.
Верно ли утверждение, что «Если ранг матрицы не совпадает с количеством ее строк, то она вырождена»
1. Нет
2. Не знаю
3. Да
Вопрос 7.
Собственные значения матрицы ищутся путем нахождения чисел…
1.которые при их вычитании из элементов главной диагонали приводят определитель матрицы к нулю.
2. которые при их сложении с элементами главной диагонали приводят определитель матрицы к нулю.
3. которые при их делении на элементы главной диагонали приводят определитель матрицы к нулю.
4. которые при их умножении на элементы главной диагонали приводят определитель матрицы к нулю.
Вопрос 8.
Для невырожденной матрицы количество собственных значений может быть … ее ранга
1.больше
2. меньше
3. больше или равно
4. меньше или равно
Вопрос 9.
Пара <собственное значение | вектор> для матрицы называется ее …
1. рангом
2. радугой
3. спектром
4. числами
Вопрос 10.
Если исходная величина измеряется в «куб.см.», то ее абсолютная погрешность измеряется в…
1. %
2. кв. см.
3. куб.см.
Вопрос 11.
Если исходная величина измеряется в «куб.см.», то ее относительная погрешность измеряется в…
1. %
2. кв. см.
3. куб.см.
Вопрос 12.
Определите нижнюю границу изменения числа х=12,3456 с точностью до Δх=0,002:
1. 12,3457
2. 12,35
3. 12,344
4. 12,348
Вопрос 13.
Определите верхнюю границу изменения числа х=12,3456 с точностью до Δх=0,002:
1. 12,3457
2. 12,35
3. 12,344
4. 12,348
Вопрос 14.
Известно, что концентрация вещества М была измерена в зависимости от времени t.
Как удобнее отображать график?
1. Концентрация М – на оси ординат, Время t – на оси абсцисс
2. Концентрация М – на оси абсцисс, Время t – на оси ординат
3. Концентрация М и Время t – на оси абсцисс
4. Концентрация М и Время t – на оси ординат
Вопрос 15.
Известно, что концентрация вещества М была измерена в миллимолях. На оси, соответствующей изменению вещества М стоят целые числа. Какая надпись для оси будет верной?
1.М*10-3 молей
2. М*103 молей
3. М*10-2 молей
4. М*102 молей
Вопрос 16.
Известно, что концентрация вещества М имеет вид: М=1,5*е-0,23t. Как называется закон изменения вещества М?
1.Эмпирический
2. Эквивалентный
3. Экспоненциальный
4. Энергетический
Вопрос 17.
Известно, что концентрация вещества М подчиняется закону: М=1,5*е-0,23t. Исходя из него, какова начальная концентрация вещества?
1. 0,23
2. -0,23
3. -1,5
4. 1,5
Вопрос 18.
Известно, что концентрация вещества М подчиняется функциональному закону: М=1,5*е-0,23t. Определите тип функции
1. возрастающая
2. убывающая
3. константа
4. скачкообразная
Вопрос 19.
Известно, что концентрация вещества М подчиняется функциональному закону: М=1,5*е-0,23t. Предполагая, что время бесконечно, к какой величине устремится значение концентрации вещества М?
1.бесконечно большому
2. бесконечно малому
3. положительной бесконечности
4. отрицательной бесконечности
Вопрос 20.
Известно, что концентрация вещества М имеет вид: М=1,5*е-0,23t. Предполагая, что ось абсцисс – это время t, а ось ординат – Ln(M), как будет изображен график изменения вещества М в зависимости от времени.
1.как парабола
2. как кубическая парабола
3. как экспонента
4. как линия
Вопрос 21.
Известно, что концентрация вещества М имеет вид: М=1,5*3-0,23t. Какое преобразование функции M(t) приведет ее к линейному виду?
1.еМ
2. Ме
3. Log3(M)
4. М3
Вопрос 22.
Как называется действие, приводящее исходную функцию к линейному виду?
1. линейность
2. линеаризация
3. подобие
4. однотипность
Вопрос 23.
Как называется линия для графика функции, которая лучше всего показывает тенденцию изменения функции?
1.линия сближения
2. линия приближения
3. трендовая линия
4. ориентированная линия
Вопрос 24.
Название метода наименьших квадратов происходит от задачи поиска
1. максимума суммы квадратов отклонений
2. минимума суммы квадратов отклонений
3. максимума разности квадратов отклонений
4. минимума разности квадратов отклонений
Вопрос 25.
Термин «эмпирическая кривая» соответствует построению графика по …
1.внешним данным
2. внутренним данным
3. исходным данным
4. экспериментальным данным
Вопрос 26.
Система дифференциальных уравнений, составленная для схемы процесса, показывает изменение…
1. кинетических констант
2. скоростей концентраций реагентов
3. кинетических кривых
4. скоростей роста температуры
Вопрос 27.
Верно ли утверждение «Чем выше порядок численного метода решения дифференциального уравнения, тем ближе расчетная кривая к экспериментальной кривой »
1. да
2. нет
3. не знаю
Вопрос 28.
Если первый метод аппроксимирует функцию с погрешностью 0,0001, а второй – с погрешностью 0,001, то…
1. Первый метод имеет более высокую точность
2. Второй метод имеет более высокую точность
3. Точности обоих методов совпадают
Вопрос 29.
Какое существует ограничение применимости метода Симпсона для численного расчета интеграла
1. число разбиений n – должно быть нечетным
2. число разбиений n – должно быть четным
3. ограничений нет
Вопрос 30.
Как иначе называются численные методы интегрирования
1. Линейные формулы
2. Квадратурные формулы
3. Кубатурные формулы
4. Тетраэдные формулы
Литература:
1. Голицына О.Л., Попов И.И. Основы алгоритмизации и программирования: учебное пособие. – 2-е издание. – М.: ФОРУМ: ИНФРА. – М.2006. – 432 с.
2. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики: учебное пособие для ВУЗов. – М.: Астрель, 2007. - 654 с.
3. Костомаров Д.П., Корухова Л.С., Манжелей С.Г. Программирование и численные методы. – М.: Изд-во Моск. ун-та, 2001.
– 224 с.
4. Соболь Б.В., Месхи Б.Ч., Пешхоев И.М. Практикум по вычислительной математике. – Ростов-на-Дону: Феникс, 2008. – 342 с.
5. Акишин Б.А., Эркенов Н.Х. Прикладные математические пакеты. Часть 1. MathCad: учебное пособие. ‑ М.:ИП РадиоСофт, 2009.
– 132 с.
6. Сабитова Г.С. Лабораторный практикум по информационным технологиям в математике: учебное пособие для студентов 3-го курса по спец. «050201 – математика и информатика». - Стерлитамак: Стерлитамак. гос. пед. акад., 2006. – 176 с.
7. Гурский Д.А., Турбина Е.С. Вычисления в MathCad 12. – СПб.: Питер, 2006. ‑544 с.
Учебное пособие
Гиззатова Эльвира Раисовна,
Кандидат химических наук
Гнатенко Юлия Ахнафовна,
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА.
МЕТОДЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ.
Учебное пособие
Ответственный редактор – кандидат физико-математических наук, доцент Альбина Ильгизовна Карамова (Стерлитамакский филиал ФГБОУ ВО БашГУ)
Стерлитамакский филиал
Федерального государственного бюджетного образовательного учреждения высшего образования
«Башкирский государственный университет»
Гиззатова Э.Р., Борисевич С.С., Гнатенко Ю.А.
ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА.
МЕТОДЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ:
Учебное пособие
для студентов, обучающихся по направлениям
04.03.01 Химия и 03.03.02 Физика.
Стерлитамак 2016
УДК 519.6
ББК 22.192я73
Г 46
Гиззатова Э.Р., Борисевич С.С., Гнатенко Ю.А. ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА. МЕТОДЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ ДАННЫХ: учебное пособие.
Учебное пособие содержит тематический материал по основным разделам вычислительной математики, методам математической обработки информации, численным методам. Представление ведется по темам, состоящим из теоретической и практической частей. В первой из них раскрываются понятия, термины раздела, приводятся формулировки теорем. Вторая часть темы – это примеры и типовые задачи с решениями, полученными в прикладных программных обеспечениях и математических пакетах, а также задания для лабораторных работ. Пособие предназначено для студентов, обучающихся по направлению «Химия» и «Физика», и может быть использовано в качестве дополнительного материала преподавателями..
Ответственный редактор – кандидат физико-математических наук, доцент А.И. Карамова (Стерлитамакский филиал ФГБОУ ВО «БашГУ»)
Рецензенты:
кандидат технических наук Т.М. Левина (филиал ФГБОУ ВО УГНТУ в г. Салавате); кафедра математического моделирования (Стерлитамакский филиал ФГБОУ ВО БашГУ); кафедра «Общенаучных дисциплин» (филиал ФГБОУ ВО УГНТУ в г. Салавате).
© Э.Р. Гиззатова, С.С. Борисевич, Ю.А. Гнатенко, 2016
ТЕМА 1. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И ПОГРЕШНОСТИ
Процесс решения задач из физики, техники, экономики или химии с помощью методов математического моделирования состоит из нескольких этапов, показанных на рисунке:
| 1. Исследование объекта и содержательная постановка задачи |
| 2. Построение математической модели |
| 3. Выбор численного метода и разработка вычислительного алгоритма |
| 4. Разработка программы на компьютере или выбор пакета прикладных программ |
| 5. Проведение вычислений и анализ результатов |
1. На первом этапе проводится исследование объекта и формулируется содержательная (физическая, техническая, экономическая, химическая и др.) постановка задачи. Для того, чтобы задачу можно было описать количественно, нужно провести качественный и количественный анализ свойств объекта и выделить основные параметры, оказывающие на них наиболее существенное влияние.
2. Следующим этапом является математическая постановка задачи, в процессе которой осуществляется построение математической модели объекта. Под математической моделью понимают систему математических соотношений (уравнений, неравенств, краевых, начальных условий), которым должна удовлетворять система основных параметров задачи или объекта. Одно из основных требований, предъявляемых к математической модели – соответствие исследуемому объекту, т.е. адекватность. Другое немаловажное требование – чтобы модель была не слишком сложной, доступной для математической обработки. Умение находить оптимальное сочетание адекватности и сложности зависит от квалификации и даже интуиции исследователя.
3. На следующем этапе необходимо найти методы (алгоритмы) решения математической задачи. В наиболее простых случаях удается построить аналитическое решение задачи. Такие решения являются наиболее привлекательными, поскольку позволяют не только количественно, но и, что не менее важно, качественно проанализировать исследуемые параметры. Но в подавляющем большинстве случаев это не представляется возможным, и для решения математической задачи применяются численные методы. На следующем рисунке приведена классификация методов решения вычислительных задач:
| Методы решения вычислительных задач |
| Аналитические |
| Численные |
| Приближенные |
| Точные |
| Алгоритмы |
| Итерационные |
| Прямые |
4. Четвертым этапом является разработка программы решения задачи на компьютере, ее тестирование и отладка. Возможно, что рассматриваемая математическая задача исследована, и для ее решения разработаны стандартные программы, которые могут существовать отдельно или входить в пакеты прикладных программ.
5. На заключительном этапе выполняют вычислительные эксперименты на компьютере и проводят анализ результатов. Если результаты не удовлетворяют исследователя, требуется совершенствование алгоритма или метода решения задачи, ее математической модели, а в некоторых случаях – корректировка содержательной постановки.
Дата: 2019-03-05, просмотров: 421.