Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Пусть требуется найти решение дифференциального уравнения:

u ’= f ( x , u )                                                   (6.1)

в виде функции u=φ(x), принимающей в точке х=х₀ заданное значение u=u₀:

u (х₀)= φ ( x ₀ )= u ₀                                                           (6.2)

Задача вида (6.1)-(6.2) называется задачей с начальными условиями или задачей Коши.

Теорема существования и единственности решения задачи Коши :

Пусть D – некоторый прямоугольник с центром в начальной точке (х₀, u ₀ ):

x₀ – a £ x £ x₀ + a, u₀ – b £ u £ u₀ + b                     (6.3)

и пусть функция f ( x , u ) и ее частная производная 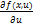 непрерывны в прямоугольнике D по совокупности аргументов x , u . Тогда можно указать отрезок

x ₀ – с £ x £ x ₀ + с           (6.4)

для с < a , на котором существует единственное решение задачи Коши (6.1)-(6.2) в виде u=φ(x).

 

Теорема существования и единственности служит обоснованием постановки задачи Коши. Она показывает, что множество всех решений дифференциального уравнения (6.1), которое принято называть общим решением, зависит от одного параметра:

u=φ(x,С).

За параметр С обычно принимают начальное значение u, но не всегда. Придавая С различные значения, будут получаться из общего решения различные частные решения.

 

1. Метод ломаных Эйлера .

Пусть необходимо решить задачу Коши (6.1)-(6.2) на некотором отрезке [a,b]. Отрезок делится на n равных частей точками:

a = x ₀ < x ₁ < x ₂ < … < x_{n -1} < x_n = b .

Точки деления x_k , k=0,1,…,n будут иметь координаты:

x_k = x₀ + kh, где h=(b-a)/n.                              (6.5)

они образуют на отрезке [a,b] равномерную c етку с шагом h.

Задаче Коши (6.1)-(6.2) сопоставляется вспомогательная задача:

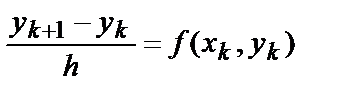 , k=0,1,…,n-1          (6.6)

y ₀ = u ₀                                                                               (6.7)

Условия разностной задачи (6.6)-(6.7) можно переписать в виде:

y ₀ = u ₀

y_{k +1} = y_k + h f ( x_k , y_k ) , k =0,1,…, n -1            (6.8)

Рекуррентная формула (5.8) позволяет по начальному значению y₀ вычислить y₁, затем по y₁ вычислить y₂ и т.д. Повторяя эту операцию n раз, последовательно определяются все y_k и строится решение задачи (6.6)-(6.7). Последовательность чисел y_k представляет собой функцию, определенную для конечного числа аргументов x_k. Такие функции называются сеточными.

Теперь решение задачи Коши (6.1)-(6.2) u(x) определим в точках x_k: u_k = u(x_k), k=0,1,…,n. Числа u_k также образуют сеточную функцию, порожденную функцией непрерывного аргумента u(x). Необходимо сравнить между собой две сеточные функции y_k и u_k.

Для этого составляются разности:

z_k = y_k - u_k , k =0,1,…, n                       (6.9)

при этом согласно (6.8)

z₀ = 0                                 (6.10)

Сеточную функцию z_k называют погрешностью решения, ее определяют по формуле:

Z = max | z_k |                       (6.11)

Рассматривая сеточную функцию

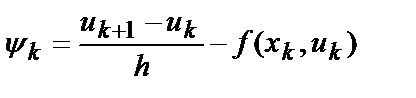           (6.12)

ее называют погрешностью аппроксимации дифференциального уравнения (6.1) разностным уравнением (6.6). За погрешность аппроксимации также берут величину:

 y = max|y_k|                                                         (6.13)

Разностное уравнение (6.6) аппроксимирует дифференциальное уравнение (6.1) с первым порядком точности относительно h . Это означает, что при h®0 величина y®0 стремится к нулю со скоростью, пропорциональной h.

Используя формулу (6.8) определяется набор точек (x_k, y_k), k=0,1,…,n. Соединяя эти точки отрезками, получается ломаная, называемая ломаной Эйлера. Она приближенно описывает решение u(x) задачи Коши : u(x) »y(x).   

Пример 6.1.

Определить численное решение дифференциального уравнения 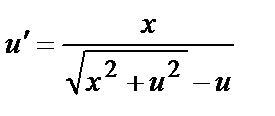 методом Эйлера на [0,1] с шагом h=0,5 и начальным условием: u(0)= - 0,5. Сравнить его с аналитическим частным решением. Найти погрешность замены аналитического решения численным решением.

Решение:

Его общее решение имеет вид: 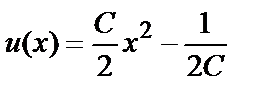. При подстановке в него u(0)= - 0,5 определяется С=1

Определим решение методом Эйлера с шагом 0,5:

y(0)=u(0)= - 0,5

y(0,5) = y(0)+0,5*f(0,-0,5)=-0,5+0,5*(0/( 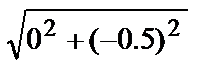 - (-0,5)) = - 0,5

y(1,0) = y(0,5)+0,5*f(0,5;y(0,5)) = - 0,5 + 0,5*(0,5/( 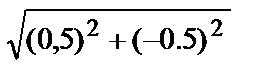 - (-0,5)) = -0,29289

 

Аналитическое решение дает значения: u(0)=-0,5; u(0,5)= -0,375; u(1,0)= 0

Расчетная таблица имеет вид:

X	y_Eiler	u_analit	z	Psi
0	-0,5	-0,5	0	0,25
0,5	-0,5	-0,375	0,125	0,249656
1	-0,29289	0	0,292893

Погрешность замены аналитического решения численным решением будет равна:

Z = max|z_k| = max{0,0.125, 0.29289}=0.29289.

Погрешность аппроксимации:

y = max|y_k| = max{0.25; 0.249656}-0.25

Соответствие решений, найденных аналитически и по методу Эйлера, показано на рис. 1.

 

 

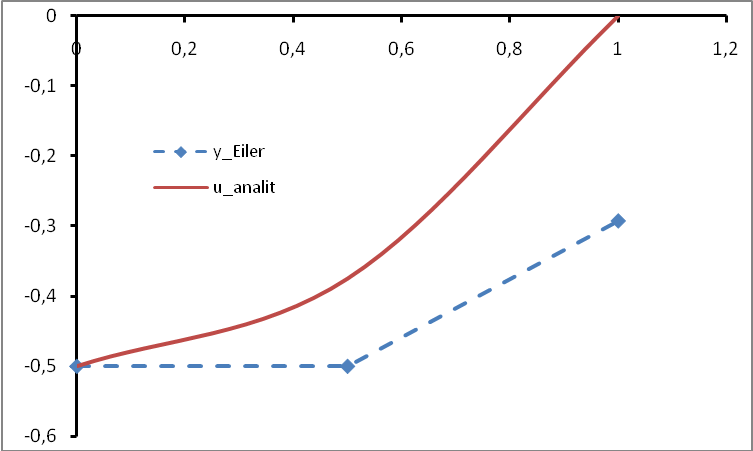
Как видно по рис.1, метод Эйлера не совпадает с аналитическим решением. Это связано с тем, что метод имеет малую точность.

Пример 6.2.

Известно, что вещество С расходуется в мономолекулярной реакции с константой скорости k=8,2*10^-2 с^-1. Начальное значение концентрации вещества С равно 10^-2.

а) составить дифференциальное уравнение по изменению концентрации вещества С в реакции. Выписать задачу Коши;

б) найти решение уравнения по методу Эйлера на временном интервале от 0 до 3 минут с шагом по времени: 1 мин и 0,5 мин;

в) построить график функции С(t) по данным, полученным методом Эйлера с шагом 1,0 и 0, 5 мин.;

г) найти максимум отклонения между численными решения уравнения методом Эйлера.

 

Решение.

а) Реакцию расходования вещества С можно описать так: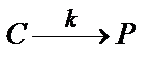   

Тогда дифференциальное уравнение по скорости расходования вещества будет иметь вид: 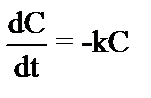 или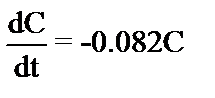

Для правильной постановки задачи Коши выпишем начальное условие: С₀=С(0) = 0,01.

 

Итак, задача Коши:

Найти решение дифференциального уравнения 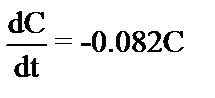при заданном начальном условии: С₀=С(0) = 0,01.

 

б) Составим таблицу расчетов по методу Эйлера с шагом t=1:

 

T

DC/dt

C (t)

0

-0,00082

Расчетная формула в ячейке C3: =C2+1*B2

0,01

1

-0,00075

0,00918

2

-0,00069

0,008427

3

-0,00063

0,007736

 

Составим таблицу расчетов по методу Эйлера с шагом t=0,5:

T	DC/dt	C (t)
0	-0,00082	0,01
0,5	-0,00079	0,00959
1	-0,00075	0,009197
1,5	-0,00072	0,00882
2	-0,00069	0,008458
2,5	-0,00067	0,008111
3	-0,00064	0,007779

 

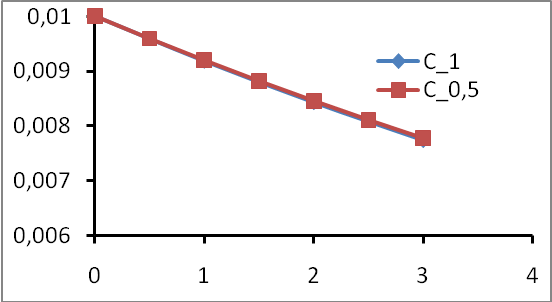
в) Построим графики по полученным таблицам в одной координатной плоскости.

По рис.2 видно, что численные решения, полученные методом Эйлера с шагом 1 и 0,5, хорошо согласуются между собой. Это говорит о гладкости функции C(t).

 

 

г) По полученным таблицам достаточно легко определить погрешность решения и погрешность аппроксимации при замене функции C(t) численными решениями.

 

Для нахождения Z сравним значения столбцов C в обоих случаях, а для нахождения y – значения столбцов dC/dt. Поскольку, максимальный шаг по t равен 1, то и сравниваемые значения будут располагаться в точках с шагом 1:

 

t	Z=|C_1-C_0.5|		T	|С'_1-C'_0.5|
0	0		0	0
1	1,681E-05		1	1,37842E-06
2	3,08914E-05		2	2,5331E-06
3	4,25764E-05		3	3,49127E-06
max=	E-05		max=	E-06

 

Найденные значения максимумов и дадут значения погрешностей решения и аппроксимации функции.