Пусть имеется некоторая область Х в пространстве переменных x 1 , x 2 ,,…, xn и известно, что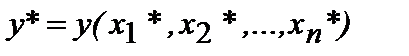 
– приближенное значение функции y (х) в области Х. Тогда предельной абсолютной погрешностью D ( y *) называют наилучшую при имеющейся информации оценку погрешности значения y *:
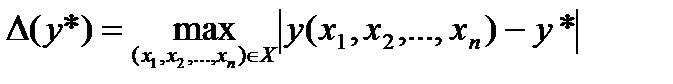(1.1)
соответственно, предельной относительной погрешностью называют величину:
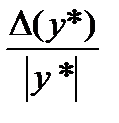(1.2)
В случае, когда область X – прямоугольник: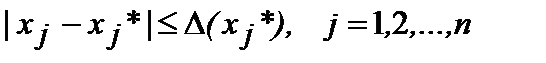 
, где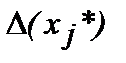 
- абсолютная погрешность переменной х j и y (х) – непрерывно дифференцируемая функция своих аргументов, то ее погрешность можно оценить как:
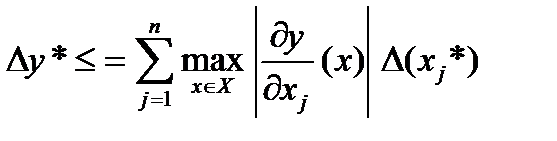(1.3)
При практической работе вместо погрешности (1.3) пользуются следующей формулой:
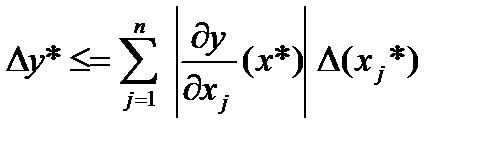(1.4)
называемой линейной оценкой погрешности.
Пример 1.8.
Вычислить погрешности функции y = ln ( sin ( x 2 )),заданной на промежутке [0.8;1.0], с шагом по аргументу D х*=0.05, х*=0.87 по формулам (1.1)–(1.4). Провести сравнительный анализ полученных погрешностей.
Решение.
Составим таблицу данных, введя в столбец А значения аргумента х, а в столбец В значения функции, согласно заданной формуле
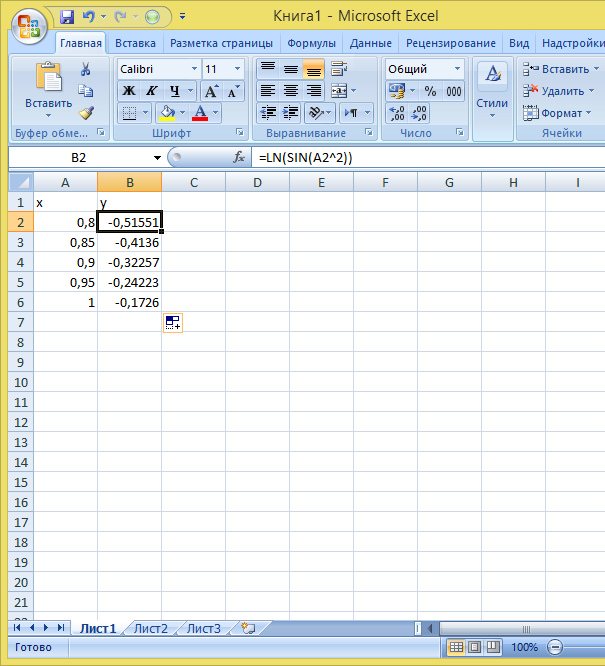
Составим столбец С как отклонения значений функции на промежутке от значения y*=y(x*)
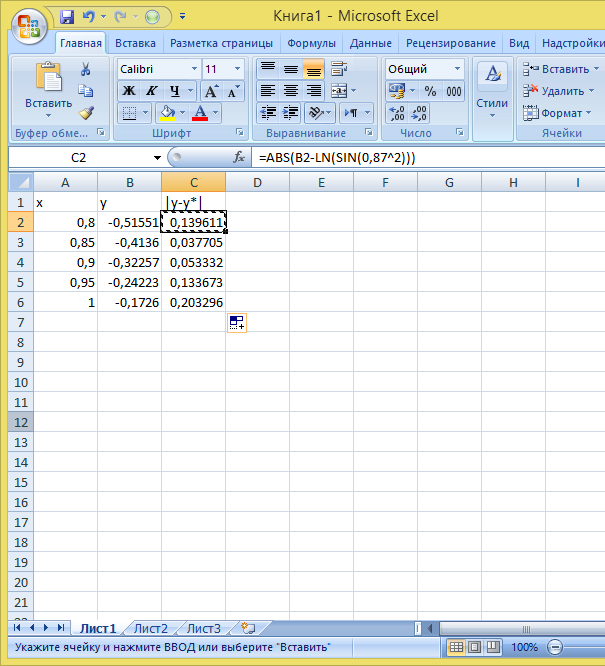
Определим максимум по столбцу С в ячейке С7: C7|=макс(С2:С6) – это предельная абсолютная погрешность функции y на промежутке [0,8:1,0]
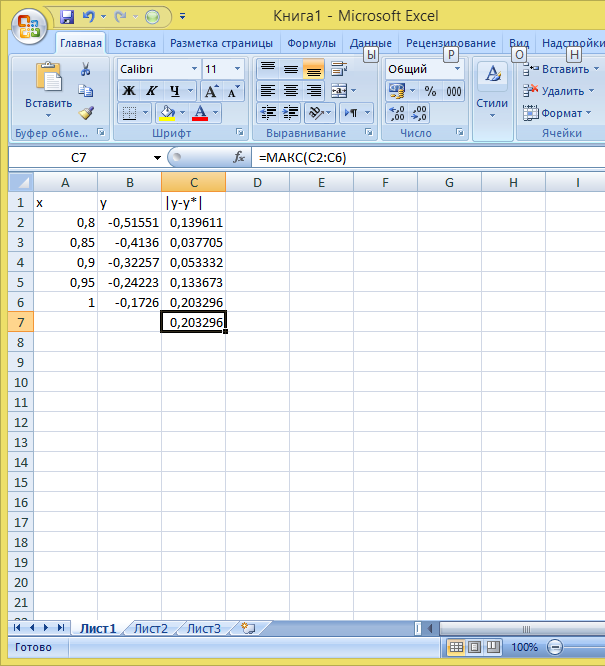
Тогда предельная относительная погрешность функции будет равна:
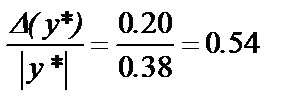
Рассчитаем другие оценки функции y по формулам (1.3) и (1.4):
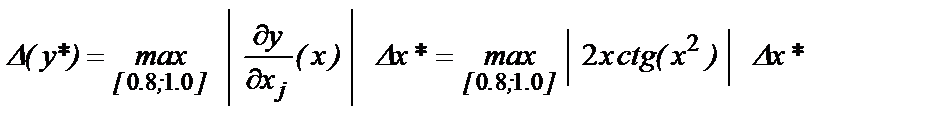
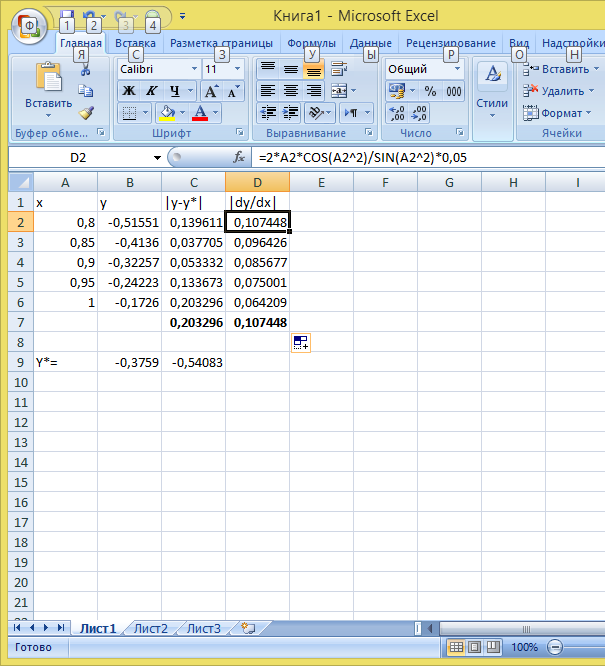
В ячейку D7 целесообразно скопировать формулу из ячейки С7, это и будет результат по формуле (3)
Далее выделим диапазон A2:D2 и скопируем его в ячейку А9, получим
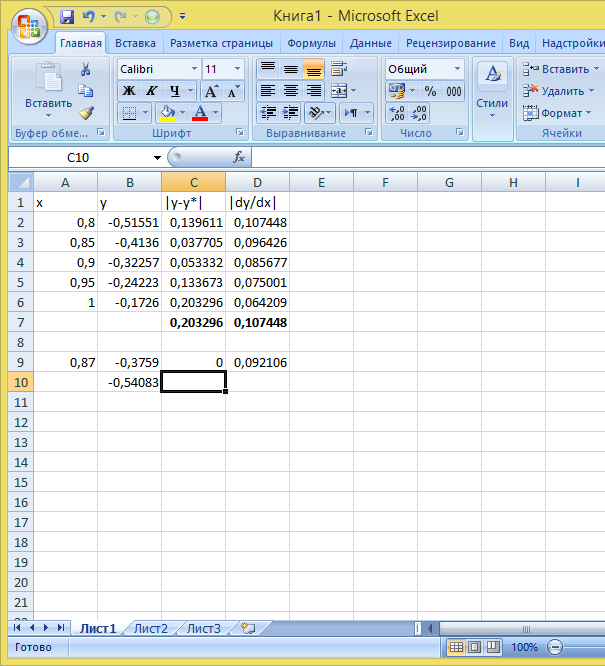
На рисунке видно, что в ячейке D9 найдена погрешность по формуле (1.4).
В ячейке B10 рассчитана относительная погрешность через формулу B10|=C7/B9
Соответственно, можно задать пределы изменения значения y ( x ) на указанном промежутке:
y ( x ) = - 0.3 8 ± 0. 20
y ( x ) = - 0.3 8 ± 0. 11
y ( x ) = - 0.3 8 ± 0. 09
Пример 1.9.
Вычислить погрешности функции z= ln ( sin ( x × y )) , заданной на прямоугольнике G =[0.8;1.0]×[0.3;0.5], D х=0.0 4 , х*=0.87, D y =0.05, y *=0.43 по формулам (1.1)–(1.4). Провести сравнительный анализ полученных погрешностей.
Решение.
Для определения погрешностей функции, зависящей от двух переменных, удобно пользоваться таблицами. Построение таблиц проведем в Excel.
Вначале рассчитаем значения функции в точках прямоугольника G:
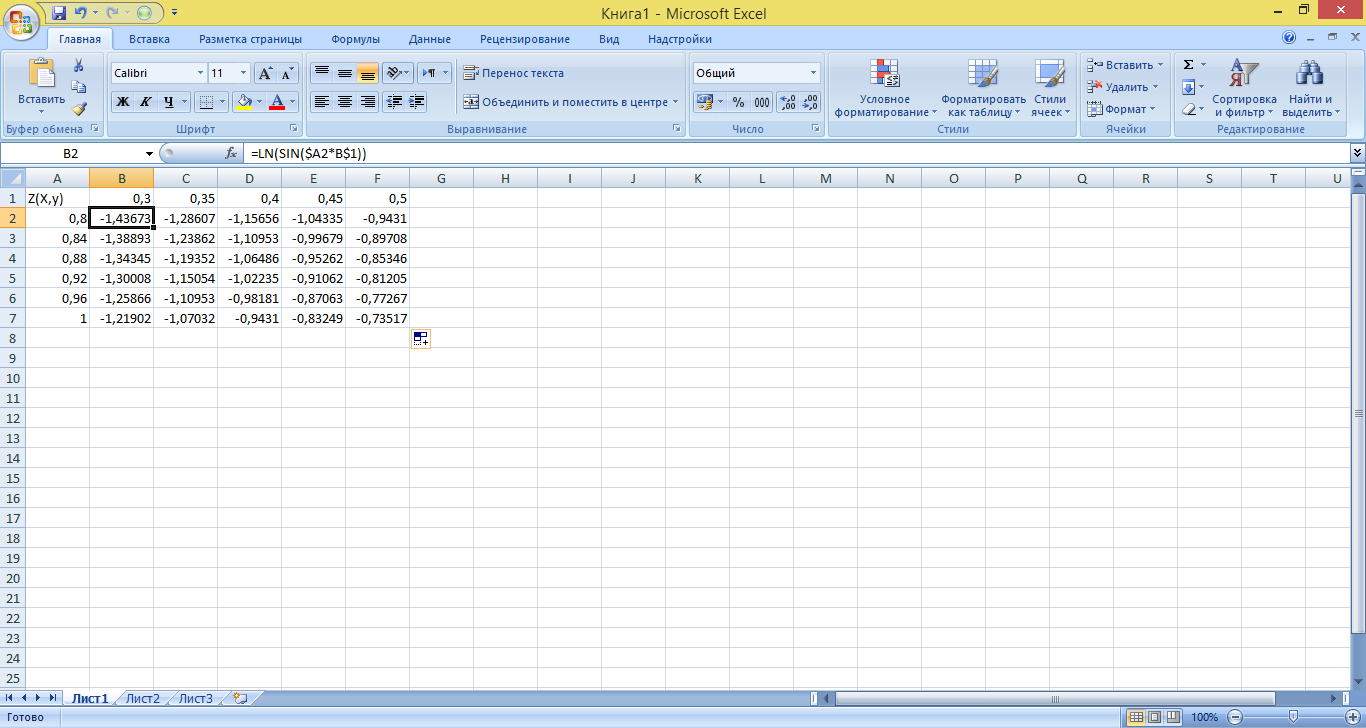
Построив таблицу отклонений значений функции:
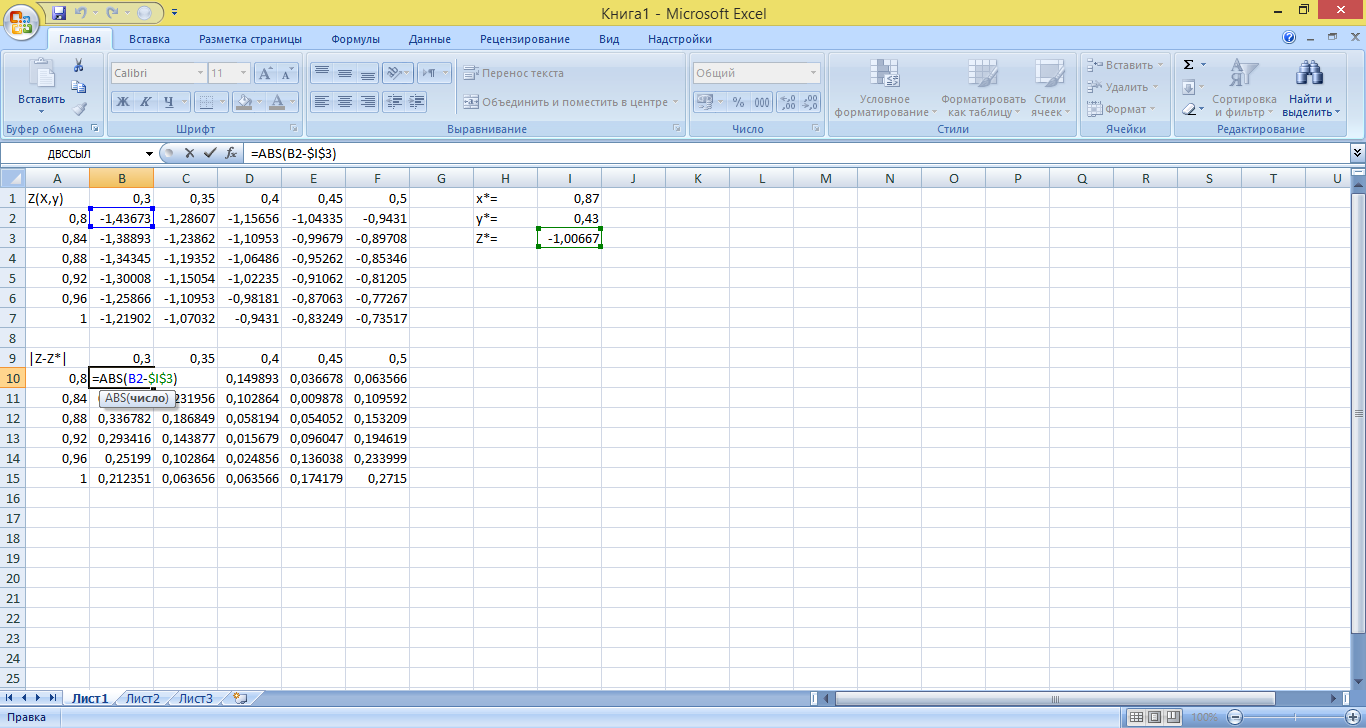
определим предельную абсолютную и относительную погрешности функции на прямоугольнике G:
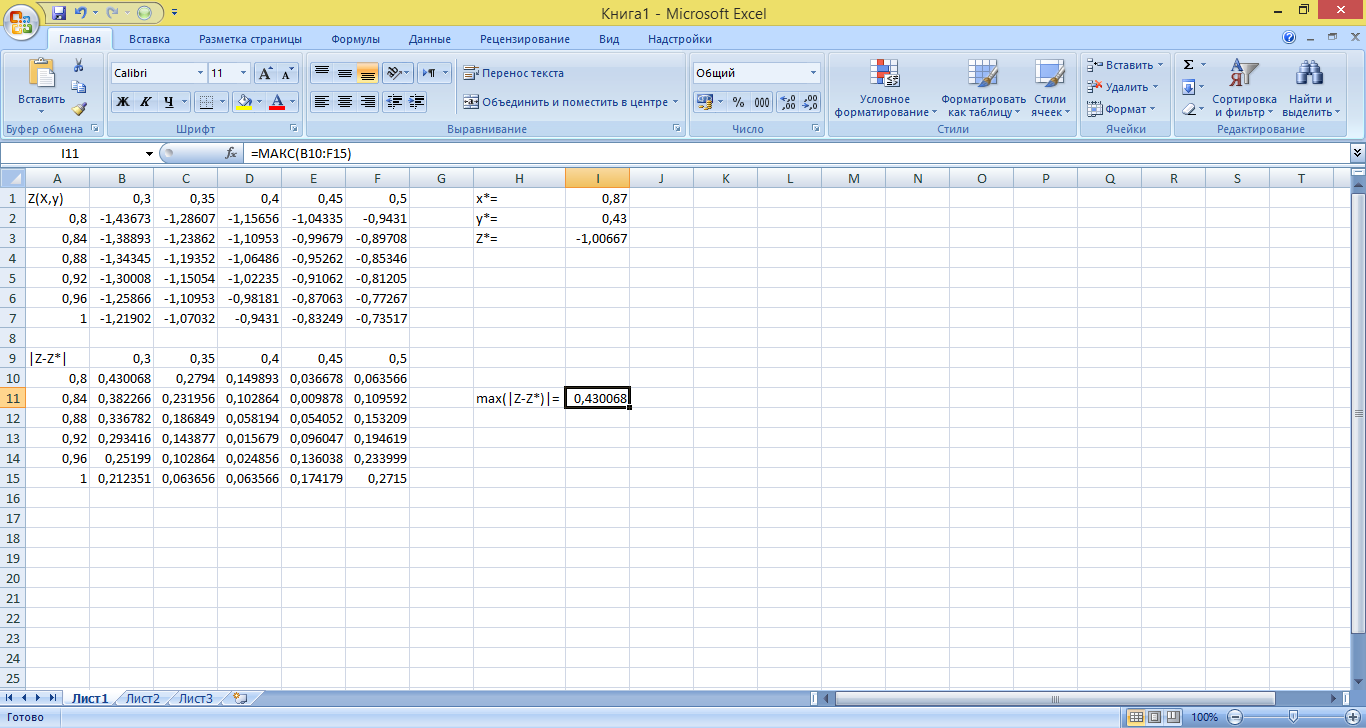
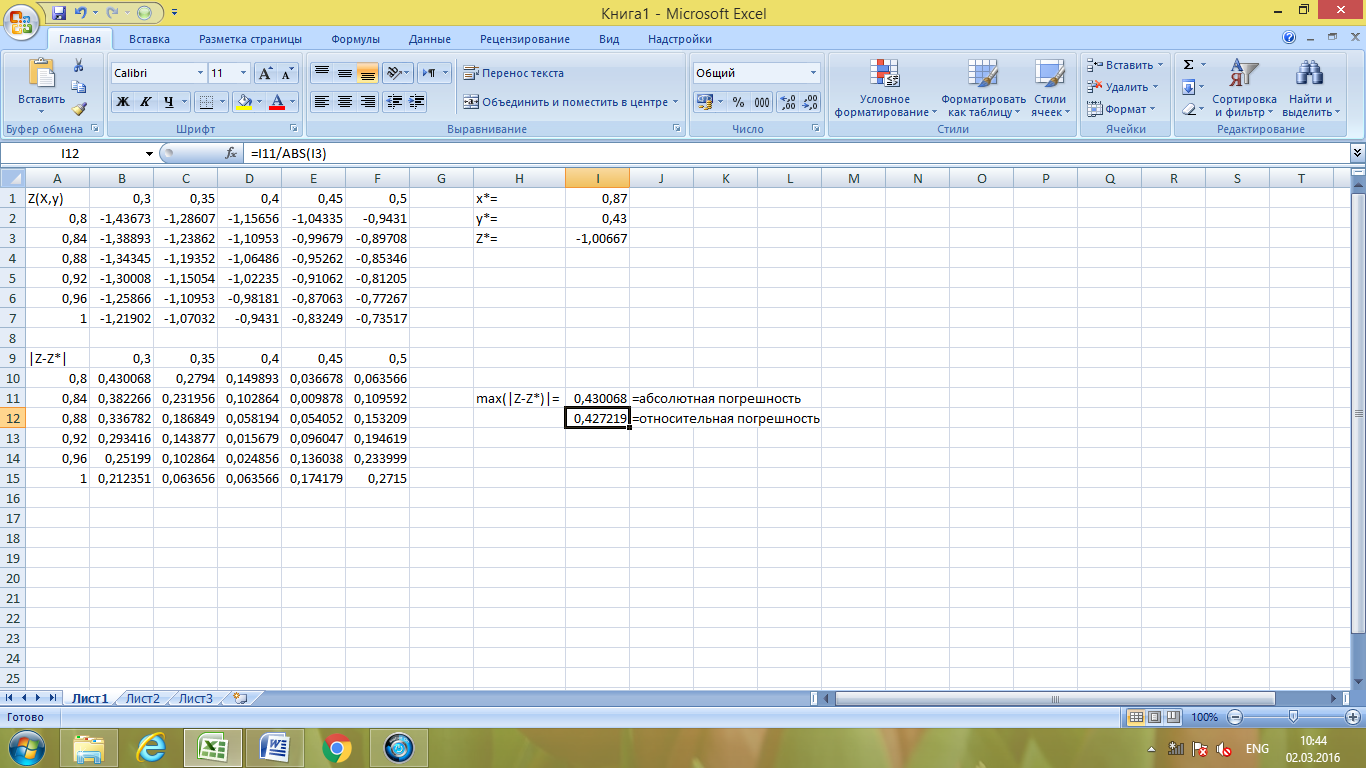
Рассчитаем другие оценки функции y, для этого построим еще две таблицы – одну по dz/dx, другую – dz/dy:
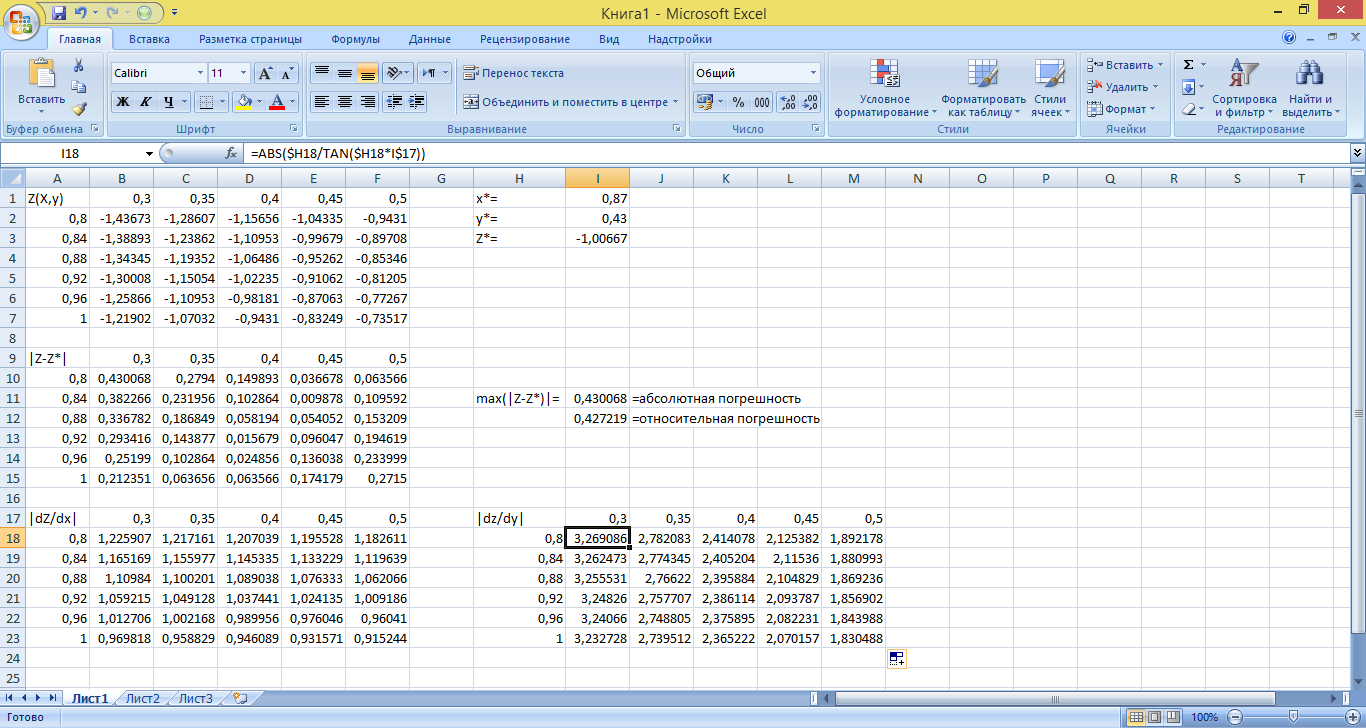
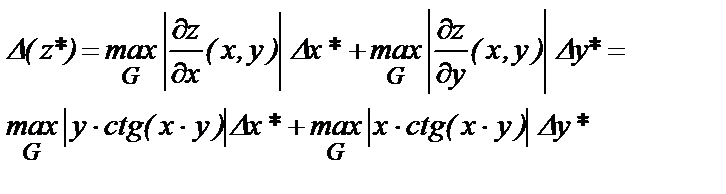
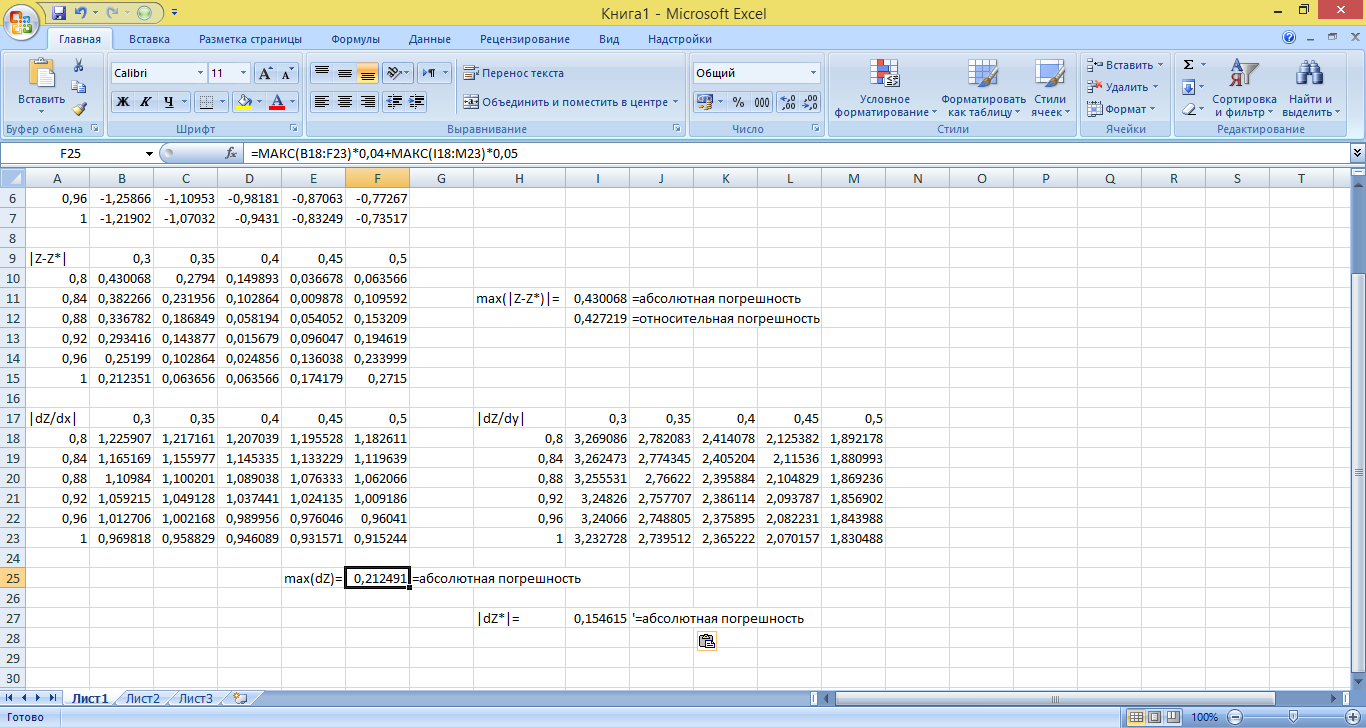
Из этой же таблицы можно определить, что по формуле (1.4) D z * есть:
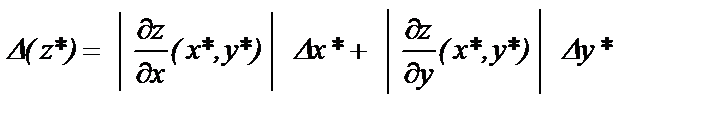
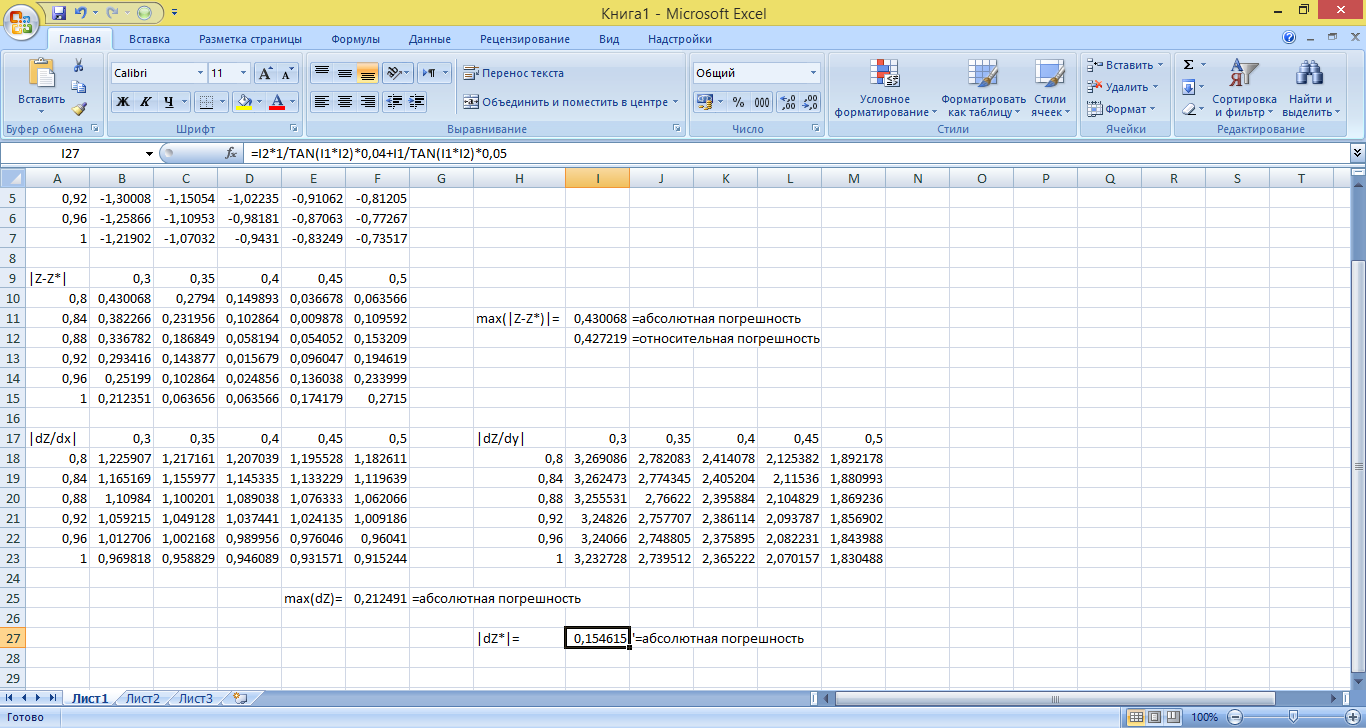
Из найденных значений, наибольшее значение оценки функции получено с использованием формулы (1.1), наименьшее по формуле линейной оценки погрешности (1.4).
Следовательно, для функции y = ln ( sin ( x × y )) на прямоугольнике G =[0.8;1.0]×[0.3;0.5], при D х=0.0 4 , х*=0.87, D y =0.05, y *=0.43 можно задать пределы изменения ее значений:
z ( x , y ) = -1 ± 0. 4
z ( x , y ) = -1 ± 0. 2
z ( x , y ) = -1 ± 0. 2
Задания для лабораторной работы №1:
Задание 1.
Вычислить погрешности следующих величин:
а) выписать абсолютную погрешность приближенного числа в виде формулы (*) и (**) Da = 0,02N31;
б) округлить число ар = 1,3N56, если абсолютная погрешность найдена двумя способами в п. а);
в) оценить (выписать через знак «±» ) величину а двумя способами, согласно решению, найденному в п б);
г)определить относительную погрешность числа ар, если абсолютная погрешность найдена по двум формулам (*) и (**) в п. а).
Задание 2.
Округлить числа:
а) ар = 23,4N4 до сотых;
б) ар = 0,0N50 до тысячных;
в) ар = 23N0N до разряда сотен.
г) ар = 23,4N4 при Da = 0,24;
д) ар = 2,N при Da = 0,03;
Задание 3.
Определить погрешность чисел:
а) ар = 3,4N в предположении, что оно записано верными цифрами в широком смысле;
б) ар = 3,4N в предположении, что оно записано верными цифрами в узком смысле.
Задание 4.
Рассчитать сумму и вычислить абсолютную погрешность; оценить сумму чисел:
Х1 = 0,N43 X2 = -3, 0N X3 = 2,N X4 = 1,03.
Задание 5.
Вычислить погрешности одномерной функции y= y ( x ) по формулам (1.1)–(1.4). Провести сравнительный анализ полученных погрешностей.
а)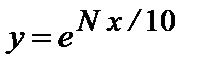 
, на промежутке [-2.0;-1.8], D x *=0.01,
х*=-1.9+ N /100.
б)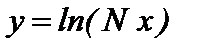 
, на промежутке [2;3], D x *=0.05, х*=2.52+ N/1000 .
в)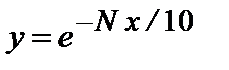 
, на промежутке [3;3.2], D x *=0. 0 1,
х*=3.1 5-N/1000 .
г)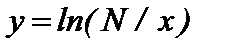 
, на промежутке [2;4], D x *= 0,2 , х*= 2,56+N/100 .
Задание 6 .
Вычислить погрешности двумерной функции z= z ( x , y ) по формулам (1.1)–(1.4). Провести сравнительный анализ полученных погрешностей.
а)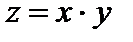 
, G =[- N ;- N +1]×[1.2;1.4], D x *=0. 0 5, х*=- N +0. 28 , D y *=0. 0 1, y *=1.3 7 .
б)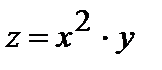 
, G =[2;2.4]×[ N /2; N /2 + 1], D x *=0. 0 2,
х*=2. 3 2 +N/1000 , D y *=0. 05 , y *=( N +1)/2 +N/1000 .
в)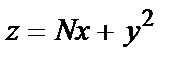 
, G =[1.0;1.6]×[0.8;1.0], D x *=0. 03 , х*=1 ,36-N/100 , D y *=0. 0 1, y *=0. 87 .
г)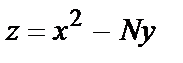 
, G =[1.2;1. 6 ]×[2.0;2.4], D x *=0. 02 , х*=1. 3+N/100 , D y *=0. 0 2, y *=2.2 45 .
Контрольные вопросы
1. Перечислите этапы решения прикладной задачи.
2. Какие причины погрешностей бывают?
3. Приведите формулу, связывающую абсолютную и относительную погрешности.
4. В чем отличие абсолютной погрешности от абсолютной предельной погрешности.
5. Какие цифры в записи числа называют верными и значащими?
6. Приведите правила округления чисел.
7. Как вычислить предельную абсолютную погрешность суммы чисел?
8. Как вычислить предельную относительную погрешность произведения?
9. Как рассчитать предельную абсолютную погрешность одномерной функции?
10. Как рассчитать предельную абсолютную погрешность двумерной функции?
Дата: 2019-03-05, просмотров: 338.
