Фокус-топ
Барлық сапалы әдістемелер ішінен соңғы кездері ең көп таралғаны фокус-топтар болып табылады. Бұл - зерттелетін объект жөнінде ақпарат алу мақсатындағы топтық пікір алысулар. Соңғысы оларды мақсаты белгілі бір көзқарастың жеңісі болып табылатын ғылыми немесе саяси пікір алысулардан өзгеше етеді.
Фокус-топтар құрамы (6-дан 12-ке дейінгі әрбір адам) зерттелетін жиынтық ішіндегі пікірлер, көңіл-күй, қажеттіліктер, талғамдар айырмашылығын барынша көрсету үшін іріктеп алынады (фокус-топты іріктеп алу рекруттеу деп аталады). Сонымен бірге, топтар ішінде жасы немесе білім деңгейі бойынша үлкен айырмашылықтарға жол берілмейді. Олай болмағанда, фокус-топтар әдісінде ақпарат алудың аса маңызды тәсілі болып табылатын топтық серпін жұмыс істемей қалуы мүмкін.
Фокус-топтар одан сайын алуан түрлі болуда және бүгіннің өзінде оларды бірнеше негіздер бойынша жіктеуге болады. Біз келесі жіктелімді ұсынамыз:
Құрамы бойынша
1-ші жіктелім (рекруттеудің күрделілігі бойынша):
| Қарапайым контингентпен (қатысушылар “бұқара” топтарын білдіреді) | Арнайы контингентпен (белгілі бір мамандық адамдары, белгілі бір қызмет пен сала қызметкерлері) | Қол жеткізу қиын немесе элита контингентпен |
2-ші жіктелім (қатысушылардың біркелкі немесе біркелкі емес деңгейі бойынша):
| Гомогенді (толығымен немесе көбінесе белгілі бір топ көрсетілген: жас өспірімдер, жастар, әйелдер, зейнеткерлер және т.б.) | Гетерогенді (әр түрлі әлеуметтік-демографиялық және әлеуметтік-кәсіби топтар көрсетілген) |
3-ші жіктелім (өзіндік немесе топтық /корпоративтік көзқарастары мен қызығушылықтарының көрсетілуі бойынша:
| Өзін-өзі білдіретін қатысушылар | Ұйымдарды білдіретін қатысушылар |
Рекруттеу әдісі бойынша:
| “Көшеден”, кездейсоқ рекруттелгендер | Белгілі бір өлшемдер бойынша (мысалы, кәсі-бі, кәсіпорынның көлемі немесе меншік түрі) рекруттелгендер | Арнайы нұсқаулар бойынша рекруттелгендер (белгілі бір ком-пания қызметкерлері, қандай да бір оқиғаға қатысушылар) |
Мақсатты нұсқаулар мен өткізілу техникасы бойынша:
| Қоршаған орта проблемасын талқылау | Оқиғаларды, фактілерді талқылау | Өзіндік көңіл-күйлерді, әсер-лерді, өзінің өмір стилін талқылау | Тауар үлгілері мен жарнамалық өнімдерді тестілеу |
Фокус-топтың жүргізушісі модератор деп аталады. Модератордың жұмысы жоғары біліктілікті қажет етеді, көбінесе фокус-топты кәсіби психологтар немесе әлеуметтанушылар жүргізеді. Модераторда терең сұхбатта гайд деп аталатын пікір алысудың жалпы жоспары болады. Бірақ, терең сұхбатқа қарағанда, фокус-топта гайд одан да төмен нақтыланған. Әдетте, ол компьютермен терілген мәтіннің 2 бетін алады. Фокус-топтың өзі 2-2,5 сағат жүргізіледі. Бұл модератордың суырып салма қабілетінің үлкен рөлін көрсетеді. Модератор фокус-топтың қымбат уақытын тек қана зерттеу мақсаттары үшін пайдалануды қамтамасыз етіп, қызықты пікірталас тудырып, әрбір қатысушыдан барынша көбірек пайдалы ақпаратты “сығып алып”, гайдтың барлық сұрақтары бойынша “пікірлер таратуды” белгілеуі тиіс. Әсіресе кез келген топта таныс емес адамдар арасындағы әңгімеде кездесетін “лидерді басу” міндетті түрде қиындыққа әкеледі. Модератор тең шамада, пікір алысу үшін барлық қатысушыларды әңгімеге тартуы тиіс, өйткені олардың әрқайсысы ақпараттың бірегей қайнар көзі болып табылады.
Фокус-топтар аудио немесе бейнепленкаға жазылады, жазбалар негізінде арнайы әдістемен түсіндіру (транскриптер), резюме мен есептер дайындалады.
Бақылау
Әлеуметтану бақылауы өзінің әр түрінде зерттеушіге сандық, сол сияқты сапалық, кейде екеуінің бір жиынтығында ақпарат береді. Ақпарат жинау процестер мен құбылыстарды визуалды және есту арқылы қабылдауға негізделген. Бақылаудың ерекше белгісі оны, әдетте, басқа әдістермен бір жиынтықта пайдалану болып табылады.
Бақылауды, әдетте, рәсімнің формализмге негізделу деңгейі, бақылаушының орны, ұйымдастыру жағдайлары, жүргізудің жүйелілігі бойынша жіктейді. Бірінші негіздеме бойынша бақылау стандартты және стандартты емес болып бөлінеді. Стандартты бақылауды арнайы жоспар бойынша зерттелетін объектінің алдын ала анықталған элементтерінің тіркелуін білдіреді. Стандартты емес әдістемеде мұндай жоспар жоқ, зерттеу мақсаттары үшін маңызды жайлар бақылау процесінің өзінде айқындалады.
Бақылаушының зерттеу объектісіне қатысты жағдайына орай бақылау енгізілмеген және енгізілген (қатысушы) болуы мүмкін. Енгізілмеген бақылау кезінде зерттеуші зерттелетін объектіден тыс тұрады. Ол оқиға барысына енгізілмейді және сұрақтар қоймайды. Енгізілген бақылауда зерттеуші бақыланушылармен тікелей байланыста болады, олардың іс-әрекетіне қатысады. Енгізілген бақылау өз кезегінде жасырын (жариялы емес, құпиялы) және ашық болып бөлінеді.
Ұйымдастыру жағдайы бойынша далалық және лабораториялық бақылау бөлініп шығады. Бірінші жағдайда мәліметтер жинау кәдімгі жағдайда, шынайы өмір жағдайында, екіншісінде - жасанды түрде құрылған және бақылаушының бақылауындағы жағдайда жүзеге асырылады.
Жүйелілігі бойынша бақылау жүйелі, эпизодтық және кездейсоқ болуы мүмкін.
Бақылау әдісінің қолдану аясы айтарлықтай кең - маркетингтен бастап ғылым әлеуметтануына дейін – кіші топтарды зерттеуден бұқаралық сана мен мінез-құлықты зерттеуге дейін болады.
Дәріс 3. Математиканың әлеуметтанудағы қолданудың негізгі бағыттары
Әлеуметтану мен математиканың арақатынасы мәселелері
Веяние нового времени, бэконовские идеи опытного знания, развитие Галилеем эмпирического естествознания оказали влияние на развитие социальных наук, способствуя проникновению в них количественных методов. В середине XVII в. появляется работа В. Петти «Политическая арифметика», в которой он пишет: «...вместо того чтобы употреблять слова только в сравнительной и превосходной степени и прибегать к умозрительным аргументам, я вступил на путь выражения своих мнений на языке чисел, весов и мер (я уже стремился давно пойти по этому пути, чтобы показать пример политической арифметики), употребляя только аргументы, идущие от чувственного опыта, и рассматривая только причины, имеющие видимое основание в природе. Те же, которые зависят от непостоянства умов, мнений, желаний и страстей отдельных людей, я оставляю другим. Замечания или положения, выражаемые посредством числа, весов и мер, на которых я основывал нижеследующие рассуждения, являются или верными .или не явно ложными».
Как известно, К. Маркс назвал В. Петти «изобретателем статистики». Однако как самостоятельная наука статистика сформировалась много позднее, а у В. Петти и в последующих работах этого направления статистика (или то, что мы называем сейчас статистикой) выступала как всеобщая социальная эмпирическая наука. Анализ становления статистики чрезвычайно важен, поскольку ее стиль мышления, метод (в частности, идея показателя) глубоко проникли в экономику, позднее — в социологию и психологию.
В начальном этапе развития статистики определились два самостоятельных и отчасти противоположных направления — политическая арифметика в Англии, идущая от Петти и Граунта, и так называемая университетская статистика в Германии, связанная с именами Конринга и Ахенвалля. Направление Петти — числовой анализ: основная идея — вместо слов числа и пропорции. В. Петти ищет показатели, характеризующие население Лондона, и приходит к определению числа жителей этого города тремя способами: 1) по числу домов, семейств и душ, живущих в каждом из них; 2) по числу смертных случаев в благоприятные для здоровья годы и по отношению числа живущих к числу умерших; 3) по числу умерших от чумы в годы эпидемий и по отношению этого числа к числу тех, кто избежал смерти
Линия Конринга — поиск классификационных систем, систематизации категорий, характеризующих общество. Он исходит из четырех аристотелевых причин. Общество как организм имеет цель, и это конечная причина, по Аристотелю и по Конрингу. Аристотелева материальная причина, по Конрингу, связана со знанием о людях и товарах. Причина формальная—это законы страны. Причина действующая определяет конкретные пути управления обществом. Каждая из причин-категорий в свою очередь детализируется. Например, действующая причина содержит в себе субъекты управления и средства управления. Первые—это правители сами по себе; вторых подразделяют на одушевленные и неодушевленные. Главный представитель последних — деньги.
Во всех областях социологического исследования математические методы играют огромную роль — это относится как к капиталистическим, так и к социалистическим странам. В Советском Союзе большую известность получили работы А. Г. Аганбегяна, Ф. М. Бородкина, Ю. Н. Гаврильца, Т. И. Заславской, В. Н. Шубкина и других ученых. В других странах социалистического лагеря известны работы И. Краземан (ГДР), Ж. Старкова (НРБ), С. Шосткевича (ПНР), И. Матея (СРР) я др.
Арсенал применяемых в социальных науках математических средств весьма обширен и многообразен — различные методы математической статистики, теория игр, теория информации, аппарат теории устойчивости, теория марковских цепей, линейное программирование, факторный анализ, корреляционный анализ, теория графов, матричная алгебра и многое другое.
Вся история конкретных социальных исследований в нашей стране была связана со все более широким и более специализированным использованием математики. В первых конкретных социальных исследованиях 50-х — начала 60-х годов были взяты на вооружение простейшие математические и статистические средства — метод средних чисел, метод аналитических группировок, индексный метод анализа, т.е. методы так называемой дескриптивной статистики. В это же время был остро поставлен вопрос о репрезентативности исследований.
По мере развития конкретных исследований применялись все более точные математические методы анализа данных и выборки. Оперирование с большими массивами социальной информации привело к проблеме использования вычислительной техники — счетно-перфорационных и электронно-вычислительных машин.
Социологи столкнулись с необходимостью измерения качественных социальных переменных и моделирования социальных процессов и явлений. Все это вызвало большой интерес к обсуждению методологических проблем применения математики в социологии.
Работы, посвященные исследованию методологических проблем применения математики в марксистско-ленинской социологии, охватывают огромный круг вопросов, который в свою очередь требует определенной классификации. Не претендуя на бесспорность, можно выделить следующие направления среди методологических проблем применения математических методов в социологии, придерживаясь в основном хронологического порядка их постановки: во-первых, роль статистических закономерностей в конкретных социологических исследованиях; во-вторых, возможности и перспективы применения математики в марксистско-ленинской социологии; в-третьих, работы по определению основных типов задач, которые могут быть решены в социологии математическими средствами.
На страницах многих советских специальных журналов в 50-е годы шла острая дискуссия о роли познания статистических нединамических закономерностей окружающего мира. Эта дискуссия первоначально была вызвана трудностями в материалистической интерпретации квантовой механики, а затем перешла в область применения статистических закономерностей к анализу социальных явлений.
В ходе этой дискуссии сложились две точки зрения. Согласно первом статистика — это исключительно социально-экономическая наука, использующая некоторые математические методы; вторая точка зрения утверждает, что статистика — универсальная наука, изучающая массовые случайные процессы безотносительно к их специфике.
В конце концов дискуссия по проблемам статистики пришла к формулировке двух весьма важных выводов: во-первых, объективности статистических закономерностей в сфере социальной жизни общества и необходимости использования общей и математической статистики при проведении конкретных социологических исследований; во-вторых, необходимости применения математических методов к анализу социальных закономерностей.
Массовые процессы в природе и обществе различны. Те стороны массовых социальных процессов, которые получают количественное выражение, и представляют собой предмет статистики. Однако при этом неправомерно отождествление индивидуальных и случайных различий при анализе социальных данных. Необходимо строго отделять индивидуальные статистические различия от случайных, выявлять содержательную специфику случайного и статистического в социальной действительности.
Неправомерно подходить к экономическим и социальным явлениям с мерками, заимствованными из области изучения явления природы. Статистическая совокупность, с которой имеет дело социолог, существенно отличается от совокупности, с которой имеет дело натуралист. Социолог манипулирует со сводными данными: суммами, средними и т.д. Для индивидуальных событий общественной жизни отсутствуют главные признаки событий стохастической среды — независимость и равновозможность. Можно применять вариационные показатели для социальных (неслучайных) распределений. Существует мнение, что оценка результатов не может быть дана на базе вероятностных, сто-
Дәріс 4. Өлшеу сапасы. Әлеуметтанулық индекстер және шкалалар
Жиынтық мәліметтер дереккөздері
Әлеуметтанулық өлшеу. Өлшеу деңгейлері. Өлшеу сенімділігі мен валидтілігі.
Шкала түсінігі. Шкалаларды құрылымдау
Проблема измерения в науке нового времени является одной из центральных и в методологическом, и практическом отношениях. Если применение математики во многих областях естествознания уже вышло за рамки самой проблемы измерения (хотя в последней есть много нерешенных вопросов), то среди математических проблем социальных наук и, в частности, социологии вопросы измерения пока еще остаются центральными. И в последнее время они привлекают все большее и большее внимание.
Практика измерения восходит в своих началах к истокам науки, однако логические основания измерения не изучались вплоть до конца XIX -начала ХХ в., когда Гельмгольц изложил основные идеи репрезентационной теории измерения, а Гельдер развил аксиоматику измерения экстенсивных величин.
Интуитивная ясность в понимании сущности измерения не покидает нас, как только возникает речь об измерении. Однако более тщательный анализ проблем измерения сталкивается со значительными трудностями.
Мы говорим, что диаметр подшипника мы измеряем, а диаметр Луны, Солнца мы определяем, вычисляем, находим. Когда ставим отметку па экзамене, то измеряем знания студента и одновременно оцениваем их. Одно ли это и то же? Не измеряют ведь дерево вообще, а измеряют его высоту, поперечник у основания, т.е. измеряют не предмет, а его свойства и опять же не все свойства, а только те, которые можно измерить. То свойство, что дерево хвойное или лиственное, не измеряется вообще.
С развитием психологии и социологии в основном начиная с 30-х годов ХХ в. появилась острая необходимость в сравнении, сопоставлении величин аддитивности которые не удовлетворяют условиям. Это привело к созданию новой теории измерений. Идея ее была выдвинута крупнейшим современным психологом С. Стивенсом на рубеже 30-40-х годов. По Стивенсу, измерение возможно прежде всего потому, «что существует изоморфизм между свойствами числовых рядов и эмпирическими операциями, которые мы можем производить с объектами».
Измерение понимается как процесс соотнесения эмпирической системы с некоторой числовой системой. Из-за отсутствия единиц измерения таких величин, как удовлетворенность жизнью, национальное чувство и т.п., возник вопрос о специфике числовой системы, которая соотносится с эмпирической системой. Стивенс первоначально выдвинул четыре типа таких числовых систем, которые обусловили четыре соответствующие шкалы (или уровни) измерения: шкала наименований (номинальная), порядка (ординальная), интервалов (интервальная) и отношений.
Каждая шкала характеризуется соответствующими числовыми свойствами. Если производится измерение по определенной шкале, то это означает, что осуществляется изоморфизм между числовой системой шкалы и исследуемыми величинами. Сам Стивенс дал разделение шкал на основе тех математических преобразований, которые допускаются каждой шкалой.
Шкала наименований допускает операцию равенства-неравенства, т.е. ее числовая система обладает весьма слабыми свойствами. Эта шкала (или измерение по ней) дает простую классификацию объектов, например нумерацию игроков в футбольной команде. С числами, приписанными игрокам, мы не можем оперировать, как с числами в арифметике, а именно два игрока первого номера нам нe дадут игрока второго номера и т.п. Эти числа только отличают игроков друг от друга. Шкала порядка допускает операции равенства - неравенства и больше-меньше. Она представляет собой ранжирование по признаку (например, ряд металлов в химии). Примером такой шкалы может быть «измерение» критериев отношения к труду:
"Какие из указанных ниже суждений выражают ваше мнение?
1. Хороша любая работа, если она хорошо оплачивается.
2. Заработок главное, но важен и смысл работы, ее общественная значимость.
3. Нельзя забывать о заработке, но главное - смысл, содержание работы.
4. Хороша та работа, где ты приносишь больше пользы".
Шкала интервалов допускает операции равенства-неравенства, больше-меньше и равенства-неравенства интервалов, позволяя тем самым ввести единицу измерения. Шкала отношений допускает операции равенства-неравенства, больше-меньше, равенство интервалов и равенство отношений и тем самым реализует все арифметические операции. По этим последним двум шкалам производятся все физические измерения.
Различие шкал можно проиллюстрировать на nростом примере. Предположим, мы выявляем удовлетворенность работой. Если мы можем подразделить людей только на удовлетворенных и неудовлетворенных работой, то тем самым имеем номинальную шкалу удовлетворенности работой. Если можно было бы установить, насколько и во сколько раз удовлетворенность одних больше удовлетворенности других, то получили бы интервальную шкалу, а также шкалу отношений удовлетворенности работой. Данные, представленные (измеренные) по номинальной и ординарной шкалам, принято именовать качественными, а измеренные по шкалам интервальной и отношений количественными, поскольку первые две не допускают арифметических операций, а вторые — допускают В каждой шкале применяются строго установленные статистические методы.
Таблица 1
Шкалы измерения *
| Шкала | Основные эм-прирические операции | Математическая групповая структура | Допустимая статистика | Типичные примеры |
| Наименований (номинальная) | Установление равенства | Группа перестановок | Число случаев, мода, корреляция качественных переменных | Нумерация игроков футбольной команды |
| Порядковая (ординальная) | Установление отношений (больше-меньше) | Изотоническая группа | Медиана, ранговая корреляция | Ранжирование лиц по признаку |
| Интервальная | Установление равенства интервалов | Группа линейных преобразований | Среднее арифметическое, корреляция количественных переменных | Температура по Цельсию или Фаренгейту, энергия, календарные даты; баллы тестирования |
| Отношений | Установление равенства отношений | Группа подобия | Все операции математической статистики | Длина, вес, сопротивление, шкала высоты звука, шкала громкости звука |
| * Схема с небольшими изменениями заимствована из книги: Стивенс С. Экспериментальная психология, т. 1, с. 52 | ||||
Кумбс, развивая идеи С. Стивенса, предложил эквивалентный в математическом отношении подход к различению шкал посредством различения характера арифметических операций. Соответственно, каждая шкала характеризуется своей системой аксиом, которые и определяют числовые свойства шкалы. Стивенс не ставил целью дать строгую логическую формулировку шкал посредством аксиом. Формулировка аксиом для порядковой шкалы и шкалы отношений была дана Э. Найгелем. Кумбс предлагал рассматривать шкалы как математические конструкции, для которых важны два момента: объек ты и расстояния между объектами. По его мнению, можно провести классификацию шкал Стивенса как для элементов, так и для расстояний между ними.
Дәріс 5-6. Айнымалылар түрлері және олардың статистикалық сипаттамалары
1. Номиналды айнымалылар
2. Реттік айнымалылар
3. Интервалды айнымалылар
Номинальные переменные представляют минимальную информацию об изучаемом явлении. Они дают лишь набор дискретных категорий, позволяющих разграничить разные объекты. Номинальное измерение – этопростое наименование объектов в соответствии с заранее заданной схемой классификации. Например, пол - мужской и женский; национальность - русские, украинцы, немцы, англичане и т.д. Это измерение не сообщает, насколько характеристика «национальность» свойственна разным людям.Номинальное измерение дает возможность объединить объекты в классы,
где цифры просто обозначают категории классификации безотносительно к порядку их расположения. Измерение средней тенденции происходит путем исчисления моды. Мода - это наиболее часто встречающееся значение признака. Если в распределении признака наблюдается одно значение моды, то распределение называется унимодальным, если несколько, – полимодальным. Когда две категории обладают равным количеством случаев (наибольших), то распределение будет бимодальное.
Для того чтобы определить, насколько типична мода для нашего распределения, вычисляем дисперсию.
Значение коэффициента вариации колеблется между нулем, когда все случаи принимают одно и то же значение, и единицей, когда каждый случай имеет свое значение. Чем меньше коэффициент вариации, тем типичнее мода. В случае полимодального распределения для расчета величины ν выбирается одно из модальных значений, вокруг которого производятся вычисления.
При использовании номинальных переменных следует основываться на взаимоисключающих и исчерпывающихся категориях. Это означает, что невозможно отнести один объект к более чем одной категории, но при этом каждый объект обязательно должен быть отнесен к какой-либо категории.
Порядковые переменные
Порядковые переменные дают возможность не только категоризировать, но и упорядочивать, или ранжировать значения. При порядковых измерениях можно присваивать каждому объекту число, которое обозначает как именно данный объект связан с другими в терминах количества того конкретного свойства, которым он характеризуется. При этом возникает возможность расположить объекты по порядку, в зависимости от количества свойства, которое их характеризует.
Например, понятие «социальный класс» имеет три порядковых уровня: низший, средний, высший. В порядковых измерениях должно быть не менее трех классов, при этом расстояние между классами не устанавливается, известно только, что они образуют некую последовательность. От классов легко перейти к числам, если условиться считать: низший класс получает ранг 1; средний - ранг 2; и так далее или наоборот. Чем больше классов в шкале, тем больше возможностей для математической обработки полученных данных.
Средняя тенденция порядковых переменных определяется медианой.
Медиана – это значение признака в упорядоченном ряду, до и после которого находится равное количество признаков. Вычисление медианы требует отсчитать с обоих концов распределения признака равное количество до тех пор, пока мы не дойдем до серединного, который и определяет значение медианы.
Если в ряду значений признаков четное число членов (2k), медиана равна среднему арифметическому из двух серединных значении признака. При нечетном числе членов (2k+1) медианным будет значение признака (k+1) объекта. Например, для 100 это 50 и 51. Если они принадлежат одному значению признака, то оно и будет медианой, если они принадлежат разным значениям, то медианой будет среднее среди них или оба.
Пример. В выборке из 10 человек респонденты проранжированы по стажу работы на данном предприятии:
Ранг 1 2 3 4 5 6 7 8 9 10
Стаж 15 13 10 9 7 6 5 4 3 1
Серединные ранги 5 и 6, поэтому медиана равна (7+6)/2=6,5лет. Таким образом, установили, что 50% рабочих имеют стаж меньше 6,5 лет, и 50% рабочих - больше 6,5 лет.
Измерение дисперсии для порядковых переменных состоит в вычислении квантильного ранга. Квантильный ранг – это мера положения внутри распределения, означающая, какая часть значений из всей совокупности, считая от меньшего значения вверх, находится ниже
рассмотренной точки.
Среди квантилей выделяют:
персентиль, деление совокупности на сто равных частей так, что первый персентиль - такое значение в этой совокупности (считая от меньшего значения вверх), ниже которого находится 1% всех случаев;
дециль - деление совокупности на десятые доли;
квинтиль - деление совокупности на пятые доли;
квартиль - деление совокупности на четверти.
Любой из указанных квантилей может быть использован для определения дисперсии порядковой величины вокруг медианы, хотя чаще используют децильные и квинтильные ранги.
Интервальные переменные
Интервальные переменные представляют наиболее полную количественную информацию об измеряемых данных. Исследователь получает возможность не только классифицировать и упорядочивать объекты, но и устанавливать, насколько большим или меньшим количеством измеряемого свойства по сравнению с другими объектами они характеризуются.
Интервальные измерения основаны на представлении о существовании некоторой стандартной единицы измеряемого свойства.
Значения, полученные по результатам интервальных измерений, могут быть подвержены любым арифметическим операциям.
Главной единицей для интервальных данных является среднее арифметическое значение, которое определяет среднюю тенденцию. Среднее арифметическое значение есть частное от деления суммы всех значений признака на их число.
Дәріс 7. Мәліметтерді жинау мен талдаудағы индекстер
Жанама индекстер
Логикалық квадрат. Логикалық үшбұрыш.
Жиынтықты бағалау шкаласы. Уақыт бюджетіндегі, мемлекеттік статистикадағы индекстер
Дәріс 8. Өлшеудің кейбір ерекше амалдары
Семинар/практикалық/ зертханалық сабақтары 7.
Луи Тернстоун шкаласы.
Эмори Богардус шкаласы.
Луи Гутманн шкалограммды талдауы
Дәріс 9. Психологиялық тесттер және социологиялық шкалалар
Впервые идею тестов выдвинул английский биолог Ф. Гальтон. Ему же принадлежит заслуга создания техники изучения индивидуальных различий на основе использования статистического метода. Гальтон искал способ математического описания тех закономерностей, которым подчиняются индивидуальные различия. В качестве метода он применил вариационную статистику.
В своих исканиях он опирался на работы А. Кетле – одного из создателей современной статистики. В своей работе «Социальная физика» (1835) Кетле показал, что формулы теории вероятности позволяют обнаружить факт подчинения поведения людей некоторым закономерностям. При анализе статистического материала он получил постоянные величины, дающие количественное описание таких актов человеческого поведения, как вступление в брак или самоубийство.
В интерпретации полученных данных Кетле исходил из идеи «среднего человека» – некоего идеала, отклонение которого изображается нормальным законом распределения. Если средняя является постоянной, то за ней должна стоять некая реальность, что позволяет предсказывать явления на основе статистических законов. Чтобы найти эти законы, безнадежно изучать каждого индивида в отдельности. Следует изучать поведение большой массы людей, используя метод вариационной статистики.
Давая статистический анализ биографических данных, Гальтон предлагал использовать законы Кетле для распределения человеческих способностей. Он считал, что существует средняя величина умственных способностей, так же как и средний рост.
Испытания, проводившиеся в антропологической лаборатории, организованной Гальтоном на Международной выставке в Лондоне в 1884 г., он назвал психологическими тестами. В широкий оборот этот термин вошел после выхода в свет в 1890 г. статьи его ученика – американского психолога Дж. М. Кеттелла – «Психологические тесты и измерения». В этой статье Кеттелл выдвинул требование статистического подхода – применения серии тестов к большому числу индивидов, полагая, что психология не сможет стать такой же точной наукой, как науки физические, если не будет базироваться на эксперименте и измерении.
Определенный сдвиг в этом направлении, по его мнению, может быть сделан путем применения серии психологических тестов к большому числу индивидов.
Разработанные Гальтоном приемы вариационной статистики вооружили психологию важным методическим средством. Среди них наиболее перспективным оказался метод исчисления коэффициента корреляции между переменными. Этот метод, усовершенствованный английским математиком К. Пирсоном и другими последователями Гальтона, внес в психологическую науку ценные математические методики, в результате использования которых возник в дальнейшем факторный анализ (работы Ч. Спирмена, Э. Л. Торндайка, Л. Терстона и др.). Постепенно совершенствовались методы статистической обработки результатов, контроля их надежности, обоснованности.
Начиная с 1905 г. французский психолог А. Бине в сотрудничестве с врачом Т. Симоном выполнили серию экспериментов по изучению умственных способностей людей различных возрастов. Проведенные на многих испытуемых (и тем самым подчиненные статистическим критериям), эти эксперименты превратились в тесты для определения уровня умственного развития. Индивидуальные различия испытывались уже не сами по себе, а в их отношении к возрастному ряду. Так возникла метрическая шкала интеллекта Бине – Симона, которая явилась первым стандартизированным тестом не только по унификации заданий и процедур их выполнения, но и по оценке полученных показателей. Это побудило ввести понятие умственного возраста – МА (Mental Age) в отличие от хронологического возраста – СА (Chronological Age). Их несовпадение считалось показателем либо умственной отсталости (МА ниже СА), либо одаренности (МА выше СА).
В 1912 г. немецкий психолог В. Штерн ввел понятие «коэффициент интеллекта» Intelligence Quotient – IQ как показатель темпа умственного развития, свойственного данному ребенку:
 Коэффициент указывает на опережение или отставание умственного возраста относительно хронологического. Л. Терман, профессор психологии Стэнфордского университета в США, вместе со своими сотрудниками дважды (в 1916 и 1937 rr.) осуществил переработку шкалы Бине – Симона. Так возникла известная шкала Стэнфорд – Бине.
Коэффициент указывает на опережение или отставание умственного возраста относительно хронологического. Л. Терман, профессор психологии Стэнфордского университета в США, вместе со своими сотрудниками дважды (в 1916 и 1937 rr.) осуществил переработку шкалы Бине – Симона. Так возникла известная шкала Стэнфорд – Бине.
В связи с тем, что интеллект, как полагали, есть нечто увеличивающееся вместе с возрастом ребенка, и так как согласно всем предварительным стандартным оценкам чем старше ребенок, тем лучше его характеристики почти в любом единичном умственном тесте, то вполне естественно возраст был воспринят в качестве психологической меры интеллекта.
Кроме индивидуальных тестов, подобных тестам Бине, применяющих возраст в качестве измеряющей шкалы, существуют также групповые тесты, которые применяются более широко и используют в качестве единиц измерения тестовые вопросы. Тестовый балл – это взвешенное и невзвешенное число вопросов, на которые правильно ответил индивид с некоторой поправкой на случайность правильного ответа, если это необходимо. Тесты обычно состоят из большого числа разнородных вопросов, меняющихся по трудности от очень легких до очень трудных.
В настоящее время теория тестов представляет собой хорошо разработанную дисциплину, включающую в себя целый ряд проблем. При составлении тестов, анализе и интерпретации результатов учитываются пять основных требований, по Галликсену[1]. 1) составление и отбор тестовых вопросов; 2) присвоение балла каждому индивиду; 3) определение точности (надежности или ошибки измерения) тестовых баллов; 4) определение предсказующего значения тестовых баллов (обоснованности или ошибки оценивании); 5) сравнение этих результатов с результатами, полученными при использовании других тестов или других групп испытуемых.
Нас в первую очередь будут интересовать вопросы, связанные с математической стороной техники тестирования.
Наиболее общим видом теста является тест, в котором каждый вопрос представляет определенную задачу. Балл – это число «правильных» ответов в ограниченное время. Вопросы могут быть неодинаковыми по трудности или же концентрироваться на одном уровне трудности. В последнем случае одни испытуемые имеют более высокую вероятность ответов, чем другие и, следовательно, более высокий уровень способности. Если вопросы имеют разные уровни трудности, то некоторые испытуемые могут ответить на более трудные вопросы и тем самым получить более высокий балл. Временной предел является еще одним источником разброса баллов, так как разные испытуемые работают с разной скоростью.
Самый обычный тип тестового балла – суммарный балл. Он основан на суммировании ответов определенной категории – правильных или неправильных.
Если мы предложим каждому из испытуемых тест из т вопросов, то результаты сможем представить в матрице вопросных баллов, в которой каждый столбец представляет соответствующий вопрос i, а каждая строка соответствующего испытуемого j.
| Вопросы | |||||||||||||
| a | b | c | i | N | 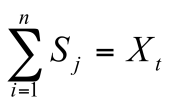
| ||||||||
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| 2 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4 |
| 3 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 |
| 4 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 5 |
| 5 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| . | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 6 |
| . | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 7 |
| J | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 9 |
| . | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 11 |
| N | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 12 |
| 10 | 9 | 9 | 7 | 6 | 6 | 5 | 4 | 3 | 3 | 2 | 1 | 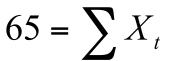
|
| 1,0 | 0,9 | 0,9 | 0,7 | 0,6 | 0,6 | 0,5 | 0,4 | 0,3 | 0,3 | 0,2 | 0,1 | 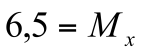
| |
Каждый испытуемый пытается ответить на каждый вопрос, и поэтому каждый вопросный балл 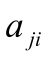 будет либо 0, либо 1. Сумма вопросных баллов в строке – это общий балл испытуемого, сумма вопросных баллов в столбце – это число испытуемых, правильно ответивших на вопрос этого столбца. Таким образом, матрица является источником информации как относительно вопросов, так и относительно испытуемых. Поделив каждую сумму вопросных баллов в столбцах на N, мы получим долю испытуемых
будет либо 0, либо 1. Сумма вопросных баллов в строке – это общий балл испытуемого, сумма вопросных баллов в столбце – это число испытуемых, правильно ответивших на вопрос этого столбца. Таким образом, матрица является источником информации как относительно вопросов, так и относительно испытуемых. Поделив каждую сумму вопросных баллов в столбцах на N, мы получим долю испытуемых 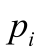 , правильно ответивших на соответствующий вопрос.
, правильно ответивших на соответствующий вопрос.
Доля тех, кто правильно ответил на определенный вопрос, является простым способом описания трудности этого вопроса. Фактически это есть средняя баллов, и чем она ниже, тем труднее вопрос.
Дәріс 10.
Статистика және әлеуметтанудағы мәліметтерді өңдеу
Слово «статистика» часто ассоциируется со словом «математика», и это пугает студентов, связывающих это понятие со сложными формулами, требующими высокого уровня абстрагирования.
Однако, как говорит Мак-Коннелл, статистика — это прежде всего способ мышления, и для ее применения нужно лишь иметь немного здравого смысла и знать основы математики. В нашей повседневной жизни мы, сами о том не догадываясь, постоянно занимаемся статистикой. Хотим ли мы спланировать бюджет, рассчитать потребление бензина автомашиной, оценить усилия, которые потребуются для усвоения какого-то курса, с учетом полученных до сих пор отметок, предусмотреть вероятность хорошей и плохой погоды по метеорологической сводке или вообще оценить, как повлияет то или иное событие на наше личное или совместное будущее, — нам постоянно приходится отбирать, классифицировать и упорядочивать информацию, связывать ее с другими данными так, чтобы можно было сделать выводы, позволяющие принять верное решение.
Все эти виды деятельности мало отличаются от тех операций, которые лежат в основе научного исследования и состоят в синтезе данных, полученных на различных группах объектов в том или ином эксперименте, в их сравнении с целью выяснить черты различия между ними, в их сопоставлении с целью выявить показатели, изменяющиеся в одном направлении, и, наконец, в предсказании определенных фактов на основании тех выводов, к которым приводят полученные результаты. Именно в этом заключается цель статистики в науках вообще, особенно в гуманитарных. В последних нет ничего абсолютно достоверного, и без статистики выводы в большинстве случаев были бы чисто интуитивными и не могли бы составлять солидную основу для интерпретации данных, полученных в других исследованиях.
Для того чтобы оценить огромные преимущества, которые может дать статистика, мы попробуем проследить за ходом расшифровки и обработки данных, полученных в эксперименте. Тем самым, исходя из конкретных результатов и тех вопросов, которые они ставят перед исследователем, мы сможем разобраться в различных методиках и несложных способах их применения. Однако, перед тем как приступить к этой работе, нам будет полезно рассмотреть в самых общих чертах три главных раздела статистики.
1. Описательная статистика, как следует из названия, позволяет описывать, подытоживать и воспроизводить в виде таблиц или графиков
данные того или иного распределения, вычислять среднее для данного распределения и его размах и дисперсию.
2. Задача индуктивной статистики — проверка того, можно ли распространить результаты, полученные на данной выборке, на всю популяцию, из которой взята эта выборка. Иными словами, правила этого раздела статистики позволяют выяснить, до какой степени можно путем индукции обобщить на большее число объектов ту или иную закономерность, обнаруженную при изучении их ограниченной группы в ходе какого-либо наблюдения или эксперимента. Таким образом, при помощи индуктивной статистики делают какие-то выводы и обобщения, исходя из данных, полученных при изучении выборки.
3. Наконец, измерение корреляции позволяет узнать, насколько связаны между собой две переменные, с тем чтобы можно было предсказывать возможные значения одной из них, если мы знаем другую.
Существуют две разновидности статистических методов или тестов, позволяющих делать обобщение или вычислять степень корреляции. Первая разновидность — это наиболее широко применяемые параметрические методы, в которых используются такие параметры, как среднее значение или дисперсия данных. Вторая разновидность — это непараметрические методы, оказывающие неоценимую услугу в том случае, когда исследователь имеет дело с очень малыми выборками или с качественными данными; эти методы очень просты с точки зрения как расчетов, так и применения. Когда мы познакомимся с различными способами описания данных и перейдем к их статистическому анализу, мы рассмотрим обе эти разновидности.
Как уже говорилось, для того чтобы попытаться разобраться в этих различных областях статистики, мы попробуем ответить на те вопросы, которые возникают в связи с результатами того или иного исследования. В качестве примера мы возьмем один эксперимент, а именно — изучение влияния потребления марихуаны на глазодвигательную координацию и на время реакции. Методика, используемая в этом гипотетическом эксперименте, а также результаты, которые мы могли бы в нем получить, представлены ниже.
При желании вы можете заменить какие-то конкретные детали этого эксперимента на другие — например, потребление марихуаны на потребление алкоголя или лишение сна, — или, что еще лучше, подставить вместо этих гипотетических данных те, которые вы действительно получили в вашем собственном исследовании. В любом случае вам придется принять «правила нашей игры» и выполнять те расчеты, которые здесь от вас потребуются; только при этом условии до вас «дойдет» существо предмета, если это уже не случилось с вами раньше.
Важное примечание. В разделах, посвященных описательной и индуктивной статистике, мы будем рассматривать только те данные эксперимента, которые имеют отношение к зависимой переменной «поражаемые мишени». Что касается такого показателя, как время реакции, то мы обратимся к нему только в разделе о вычислении корреляции. Однако само собой разумеется, что уже с самого начала значения этого показателя надо обрабатывать так же, как и переменную «поражаемые мишени». Мы предоставляем читателю заняться этим самостоятельно с помощью карандаша и бумаги.
Некоторые основные понятия. Популяция и выборка
Одна из задач статистики состоит в том, чтобы анализировать данные, полученные на части популяции, с целью сделать выводы относительно популяции в целом.
Популяцияв статистике не обязательно означает какую-либо группу людей или естественное сообщество; этот термин относится ко всем существам или предметам, образующим общую изучаемую совокупность, будь то атомы или студенты, посещающие то или иное кафе.
Выборка — этонебольшое количество элементов, отобранных с помощью научных методов так, чтобы она была репрезентативной, т.е. отражала популяцию в целом.
(В отечественной литературе более распространены термины соответственно «генеральная совокупность» и «выборочная совокупность». — Прим. перев.)
Данные и их разновидности
Данные в статистике — это основные элементы, подлежащие анализу. Данными могут быть какие-то количественные результаты, свойства, присущие определенным членам популяции, место в той или иной последовательности — в общем любая информация, которая может быть классифицирована или разбита на категории с целью обработки.
Не следует смешивать «данные» с теми «значениями», которые эти данные могут принимать. Для того чтобы всегда различать их, Шатийон (Chatillon, 1977) рекомендует запомнить следующую фразу: «Данные часто принимают одни и те же значения» (так, если мы возьмем, например, шесть данных — 8, 13, 10, 8, 10 и 5, то они принимают лишь четыре разных значения — 5, 8, 10 и 13).
Построение распределения — это разделение первичных данных, полученных на выборке, на классы или категории с целью получить обобщенную упорядоченную картину, позволяющую их анализировать.
Существуют три типа данных:
1. Количественные данные, получаемые при измерениях (например, данные о весе, размерах, температуре, времени, результатах тестирования и т. п.). Их можно распределить по шкале с равными интервалами.
2. Порядковые данные, соответствующие местам этих элементов в последовательности, полученной при их расположении в возрастающем порядке (1-й, ..., 7-й, ..., 100-й, ...; А, Б, В. ...).
3. Качественные данные, представляющие собой какие-то свойства элементов выборки или популяции. Их нельзя измерить, и единственной их количественной оценкой служит частота встречаемости (число лиц с голубыми или с зелеными глазами, курильщиков и не курильщиков, утомленных и отдохнувших, сильных и слабых и т.п.).
Из всех этих типов данных только количественные данные можно анализировать с помощью методов, в основе которых лежат параметры (такие, например, как средняя арифметическая). Но даже к количественным данным такие методы можно применить лишь в том случае, если число этих данных достаточно, чтобы проявилось нормальное распределение. Итак, для использования параметрических методов в принципе необходимы три условия: данные должны быть количественными, их число должно быть достаточным, а их распределение — нормальным. Во всех остальных случаях всегда рекомендуется использовать непараметрические методы.
Вопросы для самопроверки
1. Перечислите основные значения понятия «анализ данных».
2. Каковы уровни анализа эмпирических данных?
3. Что такое «социологические данные»? Каковы их виды?
4. Назовите основные стадии социологического исследования.
5. Что представляет собою предмет курса «Анализ данных в социологии»?
Оценка разброса
Как мы уже отмечали, характер распределения результатов после воздействия изучаемого фактора в опытной группе дает существенную информацию о том, как испытуемые выполняли задание. Сказанное относится и к обоим распределениям в контрольной группе:
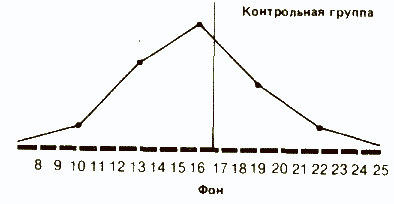
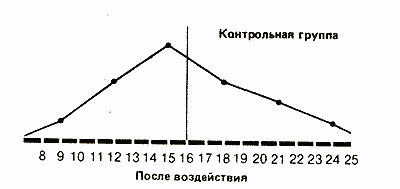
Сразу бросается в глаза, что если средняя в обоих случаях почти одинакова, то во втором распределении результаты больше разбросаны, чем в первом. В таких случаях говорят, что у второго распределения больше диапазон, или размах вариаций, т. е. разница между максимальным и минимальным значениями.
Так, если взять контрольную группу, то диапазон распределения для фона составит 22-10=12, а после воздействия 25-8=17. Это позволяет предположить, что повторное выполнение задачи на глазодвигательную координацию оказало на испытуемых из контрольной группы определенное влияние: у одних показатели улучшились, у других ухудшились. Здесь мог проявиться эффект плацебо, связанный с тем, что запах дыма травы вызвал у испытуемых уверенность в том. что они находятся под воздействием наркотика. Для проверки этого предположения следовало бы повторить эксперимент со второй контрольной группой, в которой испытуемым будут давать только обычную сигарету.
Однако для количественной оценки разброса результатов относительно средней в том или ином распределении существуют более точные методы, чем измерение диапазона.
Чаще всего для оценки разброса определяют отклонение каждого из полученных значений от средней (М-М), обозначаемое буквой d, а затем вычисляют среднюю арифметическую всех этих отклонений. Чем она больше, тем больше разброс данных и тем более разнородна выборка. Напротив, если эта средняя невелика» то данные больше сконцентрированы относительно их среднего значения и выборка более однородна.
Итак, первый показатель, используемый для оценки разброса, — это среднее отклонение. Его вычисляют следующим образом (пример, который мы здесь приведем, не имеет ничего общего с нашим гипотетическим экспериментом). Собрав все данные и расположив их в ряд
3 5 6 9 11 14,
находят среднюю арифметическую для выборки:
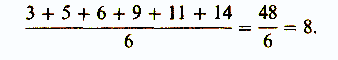
Затем вычисляют отклонения каждого значения от средней и суммируют их:
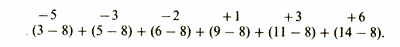
Однако при таком сложении отрицательные и положительные отклонения будут уничтожать друг друга, иногда даже полностью, так что результат (как в данном примере) может оказаться равным нулю. Из этого ясно, что нужно находить сумму абсолютных значений индивидуальных отклонений и уже эту сумму делить на их общее число. При этом получится следующий результат:
среднее отклонение равно
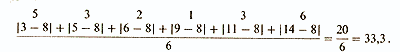
Общая формула:

где (сигма) означает сумму; |d| — абсолютное значение каждого индивидуального отклонения от средней; n — число данных.
Однако абсолютными значениями довольно трудно оперировать в алгебраических формулах, используемых в более сложном статистическом анализе. Поэтому статистики решили пойти по «обходному пути», позволяющему отказаться от значений с отрицательным знаком, а именно возводить все значения в квадрат, а затем делить сумму квадратов на число данных. В нашем примере это выглядит следующим образом:

В результате такого расчета получают так называемую вариансу. (Варианса представляет собой один из показателей разброса, используемых в некоторых статистических методиках (например, при вычислении критерия F; см. следующий раздел). Следует отметить, что в отечественной литературе вариансу часто называют дисперсией. — Прим. перев.) Формула для вычисления вариансы, таким образом, следующая:
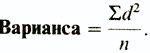
Наконец, чтобы получить показатель, сопоставимый по величине со средним отклонением, статистики решили извлекать из вариансы квадратный корень. При этом получается так называемое стандартное отклонение:

В нашем примере стандартное отклонение равно √14 = 3,74.
Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не n, а n-1:
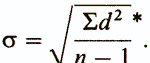
(*Стандартное отклонение для популяции обозначается маленькой греческой буквой сигма (σ), а для выборки — буквой s. Это касается и вариансы, т.е. квадрата стандартного отклонения: для популяции она обозначается σ2, а для выборки — s2.)
Вернемся теперь к нашему эксперименту и посмотрим, насколько полезен оказывается этот показатель для описания выборок.
На первом этапе, разумеется, необходимо вычислить стандартное отклонение для всех четырех распределений. Сделаем это сначала для фона опытной группы:
Вопросы для самопроверки
1. В чем сущность функционального объяснения?
2. Какие существуют типы функционализма?
3. Каковы «родовые» недостатки функционального объяснения?
4. Дайте общую характеристику теории социального действия Т. Парсонса.
5. В чем состоит сущность и какова роль «схемы AGIL» в социологии Т. Парсонса?
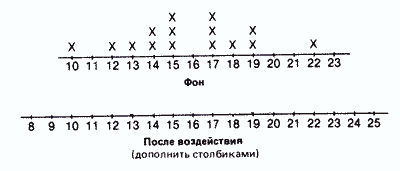
Контрольная группа
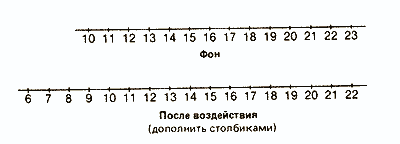
Опытная группа
Такое распределение данных по их значениям дает нам уже гораздо больше, чем представление в виде рядов. Однако подобную группировку используют в основном лишь для качественных данных, четко разделяющихся на обособленные категории.
Что касается количественных данных, то они всегда располагаются на непрерывной шкале и, как правило, весьма многочисленны. Поэтому такие данные предпочитают группировать по классам, чтобы яснее видна была основная тенденция распределения.
Такая группировка состоит в основном в том, что объединяют данные с одинаковыми или близкими значениями в классы и определяют частоту для каждого класса. Способ разбиения на классы зависит от того, что именно экспериментатор хочет выявить при разделении измерительной шкалы на равные интервалы. Например, в нашем случае можно сгруппировать данные по классам с интервалами в две или три единицы шкалы:
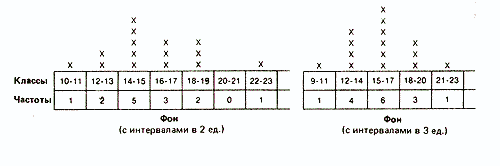
Выбор того или иного типа группировки зависит от различных соображений. Так, в нашем случае группировка с интервалами между классами в две единицы хорошо выявляет распределение результатов вокруг центрального «пика». В то же время группировка с интервалами в три единицы обладает тем преимуществом, что дает более обобщенную и упрощенную картину распределения, особенно если учесть, что число элементов в каждом классе невелико. При большом количестве данных число классов по возможности должно быть где-то в пределах от 10 до 20, с интервалами до 10 и более. Именно поэтому в дальнейшем мы будем оперировать классами в три единицы.
Опытная группа
Данные, разбитые на классы по непрерывной шкале, нельзя представить графически так, как это сделано выше. Поэтому предпочитают использовать так называемые гистограммы способ графического представления в виде примыкающих друг к другу прямоугольников:
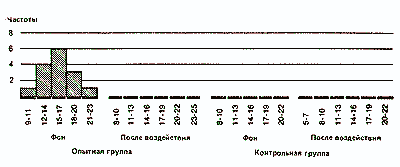
Наконец, для еще более наглядного представления общей конфигурации распределения можно строить полигоны распределения частот. Для этого отрезками прямых соединяют центры верхних сторон всех прямоугольников гистограммы, а затем с обеих сторон «замыкают» площадь под кривой, доводя концы полигонов до горизонтальной оси (частота = 0) в точках, соответствующих самым крайним значениям распределения. При этом получают следующую картину:

Если сравнить полигоны, например, для фоновых (исходных) значений контрольной группы и значений после воздействия для опытной группы, то можно будет увидеть, что в первом случае полигон почти симметричен (т.е. если сложить полигон вдвое по вертикали, проходящей через его середину, то обе половины належатся друг на друга), тогда как для экспериментальной группы он асимметричен и смещен влево (так что справа у него как бы вытянутый шлейф).
Полигон для фоновых данных контрольной группы сравнительно близок к идеальной кривой, которая могла бы получиться для бесконечно большой популяции. Такая кривая — кривая нормального распределения - имеет колоколообразную форму и строго симметрична. Если же количество данных ограничено (как в выборках, используемых для научных исследований), то в лучшем случае получают лишь некоторое приближение (аппроксимацию) к кривой нормального распределения.
Если вы построите полигон для фоновых значений опытной группы и значений после воздействия для контрольной группы, то вы наверняка заметите, что так же будет обстоять дело и в этих случаях.
Оценка разброса
Как мы уже отмечали, характер распределения результатов после воздействия изучаемого фактора в опытной группе дает существенную информацию о том, как испытуемые выполняли задание. Сказанное относится и к обоим распределениям в контрольной группе:
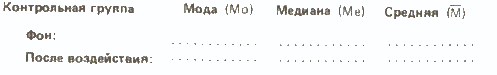


Сразу бросается в глаза, что если средняя в обоих случаях почти одинакова, то во втором распределении результаты больше разбросаны, чем в первом. В таких случаях говорят, что у второго распределения больше диапазон, или размах вариаций, т. е. разница между максимальным и минимальным значениями.
Так, если взять контрольную группу, то диапазон распределения для фона составит 22-10=12, а после воздействия 25-8=17. Это позволяет предположить, что повторное выполнение задачи на глазодвигательную координацию оказало на испытуемых из контрольной группы определенное влияние: у одних показатели улучшились, у других ухудшились. Здесь мог проявиться эффект плацебо, связанный с тем, что запах дыма травы вызвал у испытуемых уверенность в том. что они находятся под воздействием наркотика. Для проверки этого предположения следовало бы повторить эксперимент со второй контрольной группой, в которой испытуемым будут давать только обычную сигарету.
Однако для количественной оценки разброса результатов относительно средней в том или ином распределении существуют более точные методы, чем измерение диапазона.
Чаще всего для оценки разброса определяют отклонение каждого из полученных значений от средней (М-М), обозначаемое буквой d, а затем вычисляют среднюю арифметическую всех этих отклонений. Чем она больше, тем больше разброс данных и тем более разнородна выборка. Напротив, если эта средняя невелика» то данные больше сконцентрированы относительно их среднего значения и выборка более однородна.
Итак, первый показатель, используемый для оценки разброса, — это среднее отклонение. Его вычисляют следующим образом (пример, который мы здесь приведем, не имеет ничего общего с нашим гипотетическим экспериментом). Собрав все данные и расположив их в ряд
3 5 6 9 11 14,
находят среднюю арифметическую для выборки:
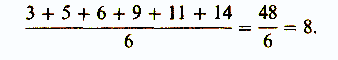
Затем вычисляют отклонения каждого значения от средней и суммируют их:
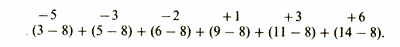
Однако при таком сложении отрицательные и положительные отклонения будут уничтожать друг друга, иногда даже полностью, так что результат (как в данном примере) может оказаться равным нулю. Из этого ясно, что нужно находить сумму абсолютных значений индивидуальных отклонений и уже эту сумму делить на их общее число. При этом получится следующий результат:
среднее отклонение равно
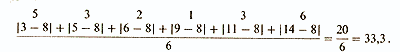
Общая формула:

где (сигма) означает сумму; |d| — абсолютное значение каждого индивидуального отклонения от средней; n — число данных.
Однако абсолютными значениями довольно трудно оперировать в алгебраических формулах, используемых в более сложном статистическом анализе. Поэтому статистики решили пойти по «обходному пути», позволяющему отказаться от значений с отрицательным знаком, а именно возводить все значения в квадрат, а затем делить сумму квадратов на число данных. В нашем примере это выглядит следующим образом:

В результате такого расчета получают так называемую вариансу. (Варианса представляет собой один из показателей разброса, используемых в некоторых статистических методиках (например, при вычислении критерия F; см. следующий раздел). Следует отметить, что в отечественной литературе вариансу часто называют дисперсией. — Прим. перев.) Формула для вычисления вариансы, таким образом, следующая:
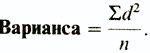
Наконец, чтобы получить показатель, сопоставимый по величине со средним отклонением, статистики решили извлекать из вариансы квадратный корень. При этом получается так называемое стандартное отклонение:

В нашем примере стандартное отклонение равно √14 = 3,74.
Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не n, а n-1:
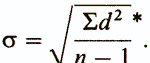
(*Стандартное отклонение для популяции обозначается маленькой греческой буквой сигма (σ), а для выборки — буквой s. Это касается и вариансы, т.е. квадрата стандартного отклонения: для популяции она обозначается σ2, а для выборки — s2.)
Вернемся теперь к нашему эксперименту и посмотрим, насколько полезен оказывается этот показатель для описания выборок.
На первом этапе, разумеется, необходимо вычислить стандартное отклонение для всех четырех распределений. Сделаем это сначала для фона опытной группы:
Метод Стьюдента (f-тест)
Это параметрический метод, используемый для проверки гипотез о достоверности разницы средних при анализе количественных данных о популяциях с нормальным распределением и с одинаковой вариансой. К сожалению, метод Стьюдента слишком часто используют для малых выборок, не убедившись предварительно в том, что данные в соответствующих популяциях подчиняются закону нормального распределения (например, результаты выполнения слишком легкого задания, с которым справились все испытуемые, или же, наоборот, слишком трудного задания не дают нормального распределения).
Метод Стьюдента различен для независимых и зависимых выборок. Независимые выборки получаются при исследовании двух различных групп испытуемых (в нашем эксперименте это контрольная и опытная группы). В случае независимых выборок для анализа разницы средних применяют формулу
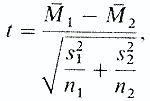
где М1 — средняя первой выборки; М2 — средняя второй выборки; s1 — стандартное отклонение для первой выборки; s2 — стандартное отклонениедля второй выборки; nl и n2 — число элементов в первой и второй выборках.
Теперь осталось лишь найти в таблице значений t (см. Приложение) величину, соответствующую n-2 степеням свободы, где n — общее число испытуемых в обеих выборках, и сравнить эту величину с результатом расчета по формуле.
Если наш результат больше, чем значение для уровня достоверности 0,05 (вероятность 5%), найденное в таблице, то можно отбросить нулевую гипотезу (Н0) и принять альтернативную гипотезу (Н1) т.е. считать разницу средних достоверной.
Если же, напротив, полученный при вычислении результат меньше, чем табличный (для n-2 степеней свободы), то нулевую гипотезу нельзя отбросить и, следовательно, разница средних недостоверна.
В нашем эксперименте с помощью метода Стьюдента для независимых выборок можно было бы, например, проверить, существует ли достоверная разница между фоновыми уровнями (значениями, полученными до воздействия независимой переменной) для двух групп. При этом мы получим:

Сверившись с таблицей значений t, мы можем прийти к следующим выводам: полученное нами значение t=0,53 меньше того, которое соответствует уровню достоверности 0,05 для 26 степеней свободы ()= 28); следовательно, уровень вероятности для такого t будет выше 0,05 и нулевую гипотезу нельзя отбросить; таким образом, разница между двумя выборками недостоверна, т. е. они вполне могут принадлежать к одной популяции.
Сокращенно этот вывод записывается следующим образом:
t=0,53; =28; р>0,05; недостоверно.
Как уже говорилось, поскольку объем выборок в данном случае невелик, а результаты опытной группы после воздействия не соответствуют нормальному распределению, лучше использовать непараметрический метод, например U-тест Манна-Уитни.
Однако наиболее полезным t-тест окажется для нас при проверке гипотезы о достоверности разницы средней между результатами опытной и контрольной групп после воздействия. Попробуйте сами найти для этих выборок значения и сделать соответствующие выводы.
Степени свободы
Для того чтобы свести к минимуму ошибки, в таблицах критических значений статистических критериев в общем количестве данных не учитывают те, которые можно вывести методом дедукции. Оставшиеся данные составляют так называемое число степеней свободы, т. е. то число данных из выборки, значения которых могут быть случайными.
Так, если сумма трех данных равна 8, то первые два из них могут принимать любые значения, но если они определены, то третье значение становится автоматически известным. Если, например, значение первого данного равно 3, а второго -1, то третье может быть равным только 4. Таким образом, в такой выборке имеются только две степени свободы. В общем случае для выборки в n данных существует п-1 степень свободы.
Если у нас имеются две независимые выборки, то число степеней свободы для первой из них составляет n1-1, а для второй — n2-1. А поскольку при определении достоверности разницы между ними опираются на анализ каждой выборки, число степеней свободы, по которому нужно будет находить критерий t в таблице, будет составлять (n1+n2)-2.
Если же речь идет о двух зависимых выборках, то в основе расчета лежит вычисление суммы разностей, полученных для каждой пары результатов (т.е., например, разностей между результатами до и после воздействия на одного и того же испытуемого). Поскольку одну (любую) из этих разностей можно вычислить, зная остальные разности и их сумму, число степеней свободы для определения критерия t будет равно n-1.
Непараметрические методы
Метод χ2 («хи-квадрат»)
Для использования непараметрического метода χ2 не требуется вычислять среднюю или стандартное отклонение. Его преимущество состоит в том, что для применения его необходимо знать лишь зависимость распределения частот результатов от двух переменных; это позволяет выяснить, связаны они друг с другом или, наоборот, независимы. Таким образом, этот статистический метод используется для обработки качественных данных. Кроме того, с его помощью можно проверить, существует ли достоверное различие между числом людей, справляющихся или нет с заданиями какого-то интеллектуального теста, и числом этих же людей, получающих при обучении высокие или низкие оценки; между числом больных, получивших новое лекарство, и числом тех, кому это лекарство помогло; и, наконец, существует ли достоверная связь между возрастом людей и их успехом или неудачей в выполнении тестов на память и т. п. Во всех подобных случаях этот тест позволяет определить число испытуемых, удовлетворяющих одному и тому же критерию для каждой из переменных.
При обработке данных нашего гипотетического эксперимента с помощью метода Стьюдента мы убедились в том, что употребление марихуаны испытуемыми из опытной группы снизило у них эффективность выполнения задания по сравнению с контрольной группой. Однако к такому же выводу можно было бы прийти с помощью другого метода — χ2. Для этого метода нет ограничений, свойственных методу Стьюдента: он может применяться и в тех случаях, когда распределение не является нормальным, а выборки невелики.
При использовании метода χ2 достаточно сравнить число испытуемых в той и другой группе, у которых снизилась результативность, и подсчитать, сколько среди них было получивших и не получивших наркотик; после этого проверяют, есть ли связь между этими двумя переменными.
Из результатов нашего опыта, приведенных в Таблице 1, видно, что из 30 испытуемых, составляющих опытную и контрольную группы, у 18 результативность снизилась, а 13 из них получили марихуану. Теперь надо внести значение этих так называемых эмпирических частот (Э) в специальную таблицу:
|
| Результаты | |||
| Ухудшение | Без изменений или улучшение | Итого | ||
| Условия | После употребления наркотика | 13 | 2 | 15 |
| Без наркотика | 5 | 10 | 15 | |
| Итого | 18 | 12 | 30 | |
Далее надо сравнить эти данные с теоретическими частотами (Т), которые были бы получены, если бы все различия были чисто случайными. Если учитывать только итоговые данные, согласно которым, с одной стороны, у 18 испытуемых результативность снизилась, а у 12 — повысилась, а с другой — 15 из всех испытуемых курили марихуану, а 15 — нет, то теоретические частоты будут следующими:
|
| Результаты | |||
| Ухудшение | Без изменений или улучшение | Итого | ||
| Условия | После употребления накортика | 18*15/30=9 | 12*15/30=6 | 15 |
| Без наркотика | 18*15/30=9 | 12*15/30=6 | 15 | |
| Итого | 18 | 12 | 30 | |
Теоретические частоты (Т)
Метод χ2 состоит в том, что оценивают, насколько сходны между собой распределения эмпирических и теоретических частот. Если разница между ними невелика, то можно полагать, что отклонения эмпирических частот от теоретических обусловлены случайностью. Если же, напротив, эти распределения будут достаточно разными, можно будет считать, что различия между ними значимы и существует связь между действием независимой переменной и распределением эмпирических частот.
Для вычисления χ2 определяют разницу между каждой эмпирической и соответствующей теоретической частотой по формуле
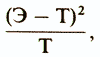
а затем результаты, полученные по всех таких сравнениях, складывают:
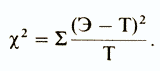
В нашем случае все это можно представить следующим образом:
| Э | Т | Э-Т | (Э-Т)2 | (Э-Т)2/Т | |
| Наркотик, улучшение | 13 | 9 | +4 | 16 | 1,77 |
| Наркотик, ухудшение | 2 | 6 | -4 | 16 | 2,66 |
| Без наркотика, ухудшение | 5 | 6 | -4 | 16 | 1,77 |
| Без наркотика, улучшение | 10 | 6 | +4 | 16 | 2,66 |
| χ=(Э-Т)2/Т= | 8,66 | ||||
Для расчета числа степеней свободы число строк в табл. 2 за вычетом единицы умножают на число столбцов за вычетом единицы. Таким образом, в нашем случае число степеней свободы равно (2- 1)*(2- 1)= 1.
Табличное значение χ2 (см. табл. в Приложении) для уровня значимости 0,05 и 1 степени свободы составляет 3,84. Поскольку вычисленное нами значение х2 намного больше, нулевую гипотезу можно считать опровергнутой. Значит, между употреблением наркотика и глазодвигательной координацией действительно существует связь. Следует, однако, отметить, что если число степеней свободы больше 1, то критерий х2 нельзя применять, когда в 20 или более процентах случаев теоретические частоты меньше 5 или когда хотя бы в одном случае теоретическая частота равна 0 (Siegel, 1956).
Опытная группа
| Фон: | 12 | 21 | 10 | 15 | 15 | 19 | 17 | 14 | 13 | 11 | 20 | 15 | 15 | 14 | 17 |
| После воздействия: | 8 | 20 | 6 | 8 | 17 | 10 | 10 | 9 | 7 | 8 | 14 | 13 | 16 | 11 | 12 |
| Знак: | - | - | - | - | + | - | - | - | - | - | - | - | + | - | - |
Итак, в 13 случаях результаты ухудшились, а в 2 — улучшились. Теперь нам остается вычислить Z для одного из этих двух значений X:

Из таблицы значений Z можно узнать, что Z для уровня значимости 0,05 составляет 1,64. Поскольку полученная нами величина Z оказалась выше табличной, нулевую гипотезу следует отвергнуть; значит, под действием независимой переменной глазодвигательная координация действительно ухудшилась.
Критерий знаков особенно часто используют при анализе данных, получаемых в исследованиях по парапсихологии. С помощью этого критерия легко можно сравнить, например, число так называемых телепатических или психокинетических реакций (X) с числом сходных реакций, которое могло быть обусловлено чистой случайностью (п/2).
Вопросы для самопроверки
1. В чем заключается сущность интерпретативной («понимающей») парадигмы?
2. Расскажите о типологии понимания. Покажите на примерах различные типы понимания.
3. Что такое очевидность? Какие типы очевидности выделяет М. Вебер?
4. Какая методологическая проблема, касающаяся предмета понимания, возникает в социологии М. Вебера, и каким образом он пытается ее решить?
Общая характеристика шкал.
Как было сказано выше, характеристики индикаторов (например, ответы на вопрос анкеты) составляют в совокупности шкалу измерения. Каждый вариант ответа представляет собою позицию шкалы измерения. Каждому уровню измерения соответствует тип шкалы измерения:
1. Номинальная шкала (шкала наименований, или назывная шкала) измеряет субъективные представления респондентов (мнения, установки, ценности, интересы и т. д.) или же признаки респондентов (паспортичка в анкете: пол, профессия, семейное положение и т. д.). Номинальная шкала не содержит сравнения (рангов) в отличие от следующего типа.
2. Порядковая (ранговая) шкала (сравнительная): объекты в этой шкале выстроены по рангу (степени). Например, вопрос «Довольны ли вы своей работой?» содержит следующие ответы (ранги): «Полностью доволен»; «Скорее доволен»; «В равной степени доволен и недоволен»; «Скорее недоволен»; «Полностью недоволен».
3. Интервальная шкала выражает те значения признака, которые можно выразить числом: возраст, стаж работы, учёба и др. Интервальная шкала может быть с а) равными и б) неравными интервалами.
К используемым шкалам измерения применяются следующие основные требования:
1. Валидность - свойство шкалы измерять именно то качество или свойство, которое социолог намерен изучать.
2. Полнота - способность шкалы учитывать все значения индикатора (например, к вопросу «Из каких источников Вы узнаёте о начале учебного года в вашем вузе?» должны быть приложены в качестве возможных вариантов ответа все источники получения информации).
3. Чувствительность - способность шкалы выявлять отношение респондентов к изучаемому явлению с той или иной степенью дифференциации. Здесь, однако, необходимо придерживаться правила «золотой середины»: малое количество вариантов ответа (например, три) не позволяет определить степень дифференциации, а большое количество (например, двенадцать) не дает провести четкую границу (т. е. отличие) между соседними вариантами ответов. Чаще всего применяют пятипозиционную (реже - семипозиционную) шкалу.
Вопросы для самопроверки
1. Расскажите об измерении (квантификации) эмпирических данных.
2. Что представляет собою основное понятие? Расскажите об интерпретации основного понятия.
3. В чем заключается сущность операционализации основного понятия?
4. Что собою представляют индикаторы и ранги?
5. Чем измеряется качество индикаторов, индексов и шкал измерения?
6. Какие существуют уровни измерения?
7. Расскажите о типах шкал измерения.
Вопросы для самопроверки
1. Назовите основные значения понятия «метод».
2. Дайте определение типологического анализа.
3. Что такое априорная типология?
4. Назовите основные понятия языка типологического анализа.
5. Назовите основные этапы ТА в нисходящей стратегии.
6. Каковы основные этапы ТА в восходящей стратегии?
Лекция 7.
Вопросы для самопроверки
1. Каковы основные значения понятия «интерпретация»?
2. Назовите уровни исходных данных при математическом анализе данных.
Лекция 8.
Пример одномерной частотной таблицы
| Значение признака | 1 | 2 | 3 | 4 | 5 |
| Частота встречаемости (%) | 20 | 15 | 25 | 10 | 30 |
Вместо процентов могут фигурировать доли: 20% заменится на 0,2, 15 - на 0,15 и т.д. (в случае такой замены мы получим числа, конечно, в большей степени похожие на вероятности, поскольку величина вероятности, как известно, изменяется от 0 до 1).
То же частотное распределение можно выразить по-другому, в виде диаграммы вида, отраженного на рис. 1 или в виде т.н. полигона распределения, рис.2.
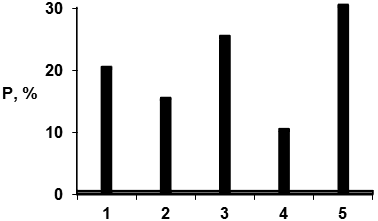
Рис.1. Диаграмма распределения, рассчитанная на основе таблицы 1.
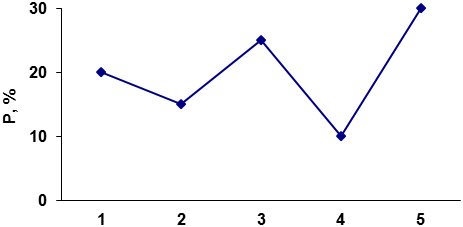
Рис. 2. Полигон распределения, рассчитанный на основе таблицы 1.
Подчеркнем, что здесь линии, связывающие отдельные точки, проведены лишь для наглядности, никакой содержательный смысл за ними не стоит (обращаем внимание читателя на то, что ниже ситуация изменится; здесь нельзя говорить об интерпретации линий из-за того, что признак – номинальный).
Казалось бы, что построение частотной таблицы или полигона распределения – дело простое, и говорить не о чем. Однако в социологии это не так. Рассмотрим проблемы, которые возникают при построении одномерных частотных таблиц. Будем учитывать тип шкалы, по которой получаются значения признака, рассмотрим номинальные, порядковые, интервальные шкалы. Однако прежде сделаем некоторое отступление для объяснения того, почему, обосновав во Введении целесообразность ограничиться номинальными данными, мы как будто отступаем от собственных принципов, переходя к шкалам более высокого типа. Дело в том, что продолжая считать номинальные данные основным объектов нашего изучения, мы не можем полностью отвлечься от других шкал. Причин тому несколько.
Во-первых, соответствующие положения фактически задействованы (иногда в неявном виде) почти во всех методах анализа, в том числе и рассчитанных на номинальные данные.
Во-вторых, хотя номинальные данные являются основным предметом изучения социолога, решение большинства задач эмпирической социологии требует “увязки” процесса такого изучения с анализом данных, полученных по шкалам высоких типов. Объясняется это тем, что именно по таким шкалам измеряются столь важные для социолога характеристики респондентов, как возраст респондента, его зарплата и т.д. Поэтому строить курс анализа данных вообще без упоминания методов изучения “числовой” информации представляется нецелесообразным.
В-третьих, хотя в литературе имеется немало работ с описанием методов статистического анализа “числовых” данных, однако при этом не всегда достаточно подробно анализируются многие их аспекты, важные для социолога-практика (например, редко затрагивается проблема разбиения диапазона изменения признака на интервалы или проблема пропущенных значений). Мы постараемся ликвидировать этот пробел хотя бы для наиболее часто используемых социологом методов – вычислении мер средней тенденции и разброса для вероятностных распределений.
Именно с “числовых” шкал мы и начнем более подробное обсуждение специфики построения распределений в социологических задачах. Приводимые ниже рассуждения справедливы для интервальныхшкал и шкал более высоких типов.
Рис. 2. Иллюстрация сущности наиболее употребительных квантилей.
Величина процента, указанная под интервалом означает долю объектов выборки, попавших в этот интервал.
Разного рода квантилями социолог пользуется очень часто. Нередко они упоминаются в средствах массовой информации (однако при этом сами термины "квантиль", "квартиль" и т.д. при этом не используются). Так, в газетах пишут о том, что, например, 10% наиболее богатых "россиян" имеют месячный доход свыше 100 тысяч рублей, а 10% наиболее бедных – ниже 300 рублей. Ясно, что 100 тысяч рублей – это девятый дециль D9, а 300 рублей – это первый дециль D1.
Медианой называется Мe = Q2 = D5 = Р50.
Нетрудно видеть, что так определенная выборочная медиана – это значение рассматриваемого признака, которое делит отвечающий этому признаку вариационный ряд (т.е. последовательность значений признака, расположенных в порядке их возрастания) пополам. Иначе говоря, медиана обладает тем свойством, что половина всех выборочных значений признака меньше нее, а половина – больше. "Правомочность" медианы в качестве представителя анализируемой группы респондентов представляется очевидной. Для того, чтобы это почувствовать, достаточно "взглянуть", скажем, на две группы, в одной из которых медиана признака "доход" равна 500 рублей, а в другой – 5000 рублей. Ясно, что вторая группа "в среднем" гораздо богаче первой.
Обычно, построив вариационный ряд, полагают, что при нечетном числе элементов в выборке медиана равна центральному члену ряда, а при четном – точке, отвечающей середине расстояния между двумя центральными членами.
Нетрудно видеть, что вычисление медианы имеет смысл только для порядкового признака (и, конечно, для интервального, поскольку любая интервальная шкала является порядковой). Это представляется очевидным: для “чисто” номинальной шкалы (т.е. для такой, при использовании которой мы не ставим своей целью отображение какого бы то ни было эмпирического отношения порядка в числовое) само выражение “объект обладает значением признака, меньшим, чем медиана” становится бессмысленным. Понятия “больше” или “меньше” в этой ситуации не существуют
Вопросы для самопроверки
1. Каковы основные значения одномерного частотного распределения?
2. Среднее арифметическое значение признака.
Лекция 9.
Вопросы для самопроверки
1. Какие меры разброса есть отвечающие модели?
2. Необходимость введения мер разбросапризнака.
Лекция 10.
Вопросы для самопроверки
1. Главные задачи анализа номинальных данных.
2. Роль номинальных данных в социологии.
Лекция 11.
Вопросы для самопроверки
1. Назовите классификацию задач анализа связей номинальных признаков.
2. Анализируйте понятие взаимодействия.
Лекция 12.
Анализ связей типа "признак – признак".
Для измерения связи между двумя номинальными признаками в литературе предлагается более сотни коэффициентов. Это является следствием того, что интересующее насявление - указанную связь (еще раз подчеркнем, что мы говоримо статистической связи, хотя в действительности нас, как правило, интересуют соответствующие причинно-следственные отношения) – оказывается возможным формализовать по-разному. И каждому способу формализации отвечает свое понимание сути искомойсвязи, своя априорная модель того, что мы хотим изучить.
Не будем описывать все известные из литературы коэффициенты рассматриваемого характера. Коснемся лишь трех подходов к измерению парной связи между номинальными признаками. Эти подходы являются наиболее употребительными на практике.
Коэффициенты связи, основанные на критерии"Хи-квадрат".
Приведем простой пример, иллюстрирующий рассматриваемыйподход к пониманию связи между двумя номинальными признаками.Предположим, что перед нами стоит задача оценки того, зависит ли профессия респондента от его пола. Пусть наша анкетасодержит соответствующие вопросы и в ней перечисляютсяпять вариантов профессий, закодированных цифрами от 1 до 5;для обозначения же мужчин и женщин используются коды 1 и 2 соответственно. Для краткости обозначим первый признак (т.е.признак, отвечающий вопросу о профессии респондента) через Y,а второй (отвечающий полу) - через X. Итак, наша задача состоит в том, чтобы определить, зависит ли Y от X.
Предположим, что исходная таблица сопряженности, вычисленнаядля каких-то 100 респондентов имеет вид:
Таблица 1. Пример таблицы сопряженности для двух независимых признаков
| Профессия | Пол | Итого | |
| 1 | 2 | ||
| 1 | 18 | 2 | 20 |
| 2 | 18 | 2 | 20 |
| 3 | 45 | 5 | 50 |
| 4 | 0 | 0 | 0 |
| 5 | 9 | 1 | 10 |
| Итого | 90 | 10 | 100 |
Вероятно, любой человек согласится, что в таком случае признаки можно считать независимыми, поскольку и мужчины, и женщины в равной степени выбирают ту или иную профессию: первая и вторая профессии пользуются одинаковой популярностью и у тех и у других; третью – выбирает половина мужчин, но и половина женщин; четвертую не любят ни те, ни другие и т.д. Итак, мы делаем вывод: независимость признаков означает пропорциональность столбцов (строк; с помощью несложиных арифметических выкладок можно показать, что пропорциональность столбцов эквивалентна пропорциональности строк) исходной частотной таблицы. Заметим, что в случае пропорциональности “внутренних” столбцов таблицы сопряженности, эти столбцы будут пропорциональны также и столбцу маргинальных сумм по строкам. То же – и для случая пропорциональности строк они будут пропорциональны и строке маригинальных сумм по столбцам.
Наука не дает точного ответа. Она предлагает нам лишь такой его вариант, который формулируется в вероятностных терминах. Этот ответ можно найти в математической статистике. Чтобы его воспринять, необходимо взглянуть на изучаемую связь, опираясь на своеобразное математико-статистическое видение мира. Опишем соответствующие рассуждения в следующем параграфе. Сразу скажем, что эти рассуждения типичны для математической статистики – речь идет об одной из основных решаемых ей задач – проверке статистической гипотезы.
Вопросы для самопроверки
1. Какие связи типа "признак – признак"?
2. Каковы коэффициенты связи, основанные на критерии"Хи-квадрат"?
3. Каковы коэффициенты связи, основанные на моделях прогноза?
Лекция 13.
Рис. 1. Схематическое изображение свойств коэффициентов Q и Ф.
Таким образом, мы видим, что Q обращается в 1, если хотя бы один элемент главной диагонали частотной таблицы равен 0. Для обращения же в 1 коэффициента F необходимо обращение в 0 обоих элементов главной диагонали. Нужны ли социологу оба коэффициента? Покажем, что каждый из них позволяет выделять свои закономерности. Или, как мы говорили выше – за каждым из них стоит своя модель изучаемого явления, свое понимание связи, выделение как бы одной стороны того, что происходит в реальности. Постараемся убедить читателя, что социолога должны интересовать обе эти стороны.
Вопросы для самопроверки
1. Каковы коэффициенты связи, основанные на понятии энтропии?
2. Каковы коэффициенты связи для четырехклеточных таблиц сопряженности?
Лекция 14.
Анализ связей типа "альтернатива – альтернатива". Смысл локальной связи. Возможные подходы к ее изучению.
При обсуждении прогнозных и информационных коэффициентов связи мы говорили о том, что знание какого-то одного значения Х может нам дать очень большую информацию об Y, а для другого значения Х аналогичная информация может быть мала. Это и означает, что для первого значения Х имеет место сильная локальная связь.
Сами термины “локальный” и “глобальный” применительно к пониманию связи между переменными, вероятно, впервые были использованы в [Чесноков, 1982].В п. 2.2.1 мы уже упоминали, что “локальному” подходу в этой работе отвечает понимание связи как некоторого отношения между двумя конкретными градациями а и b признаков Х и Y соответственно. В таком случае мы можем говорить о сильной связи, если из того, что для некоторого объекта первый признак принимает значение а, с большой вероятностью следует, что второй признак для того же объекта принимает значение b. И можно говорить о слабой связи, если аналогичная вероятность мала (еще раз напомним, что “глобальная” связь - это результат определенного “усреднения” подобных локальных связей).
Для изучения локальной связи можно использовать, например, коэффициенты Ф и Q. Для этого надо исходную частотную таблицу произвольной размерности привести к определенной четырехклеточной. Покажем на примере, как это делается. Рассмотрим частотную таблицу, выражающую зависимость между
Таблица 1.
Пример таблицы сопряженности
| Профессия | Читаемая газета | Итого | |||
| УГ | МК | Независимая | Правда | ||
| Врач | 5 | 2 | 13 | 8 | 28 |
| Токарь | 6 | 24 | 7 | 13 | 50 |
| Учитель | 9 | 0 | 1 | 0 | 10 |
| Космонавт | 2 | 1 | 4 | 5 | 12 |
| Итого | 22 | 27 | 25 | 26 | 100 |
профессией человека и читаемой им газетой (для простоты предполагаем, что каждый респондент может читать не более одной газеты). Предположим, что нас интересует локальная связь между свойством “быть учителем” и свойством “читать "Учительскую газету" (УГ)”. Упомянутая выше четырехклеточная таблица будет иметь вид:
Таблица 2.
Четырехклеточная таблица сопряженности, полученная из таблицы 1
| Профессия | Читаемая газета | Маргиналы по строкам | |
| УГ | Не УГ | ||
| Учитель | 9 | 1 | 10 |
| Не учитель | 13 | 77 | 90 |
| Маргиналы по столбцам | 22 | 78 | 100 |
Представляется очевидным, что если мы далее будем использовать коэффициенты связи, предназначенные для анализа четырехклеточных таблиц, то как раз и измерим силу нашей локальной связи.
Детерминационный анализ (ДА). Выход за пределы связей рассматриваемого типа.
В [Чесноков, 1982] для обозначения того объекта, который является носителем локальной связи, вводится понятие детерминации, обозначаемой  (отметим, однако, что мы несколько вольно трактуем указанное определение, поскольку автор названной работы принципиально отвергает связь детерминации с вероятностью, говоря только об относительных частотах; о них ниже пойдет речь, и мы их будем расценивать как выборочные оценки соответствующих условных вероятностей). Детерминация определяется как носитель локальной связи или как нечто, задаваемой двумя величинами: интенсивностью (точностью, истинностью)
(отметим, однако, что мы несколько вольно трактуем указанное определение, поскольку автор названной работы принципиально отвергает связь детерминации с вероятностью, говоря только об относительных частотах; о них ниже пойдет речь, и мы их будем расценивать как выборочные оценки соответствующих условных вероятностей). Детерминация определяется как носитель локальной связи или как нечто, задаваемой двумя величинами: интенсивностью (точностью, истинностью) 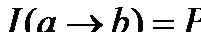 и емкостью (полнотой)
и емкостью (полнотой) 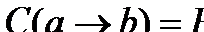 (справа стоят относительные частоты).
(справа стоят относительные частоты).
Рассмотрим приведенную выше таблицу и детерминацию (учитель® УГ). Интенсивность и емкость в этом случае будут выглядеть следующим образом:
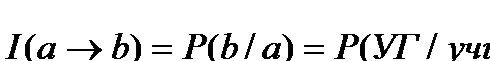
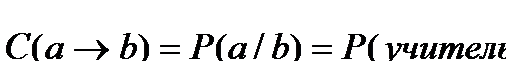
Итак, если мы хотим полностью охарактеризовать связь между свойством “быть учителем” и свойством “читать УГ”, то должны учесть два числа - долю читающих УГсреди учителей (90%) и долю учителей среди читающих УГ (41%). При всей своей простоте, это соображение далеко не всегда учитывается социологами. Частая ошибка применительно к нашему случаю означает, что исследователь узнает, что почти все учителя читают УГ и делает вывод, состоящий в том, что аудитория УГ в основном состоит из учителей. Конечно, логика здесь “хромает” - действительно, учителя составляют менее половины аудитории УГ.
Таким образом, для полного изучения "взаимодействия"двух альтернатив (т.е. изучения детерминации) необходимо принимать во внимание обе величины - и емкость, и интенсивностьдетерминации. Казалось бы, это достаточно очевидное положение.Тем не менее, социолог часто на практике про это забывает (илихочет "забыть"?!).Приведем пример того, как это обстоятельство приводит кнеправильной интерпретации исследователем имеющихся в его распоряжении данных.
После выборов в государственную Думу, прошедших в декабре1995 года, во многих средствах массовой информации обыгрывалсятот факт, что среди голосовавших за КПРФ была относительно мала доля людей с высшим образованием. Действительно, она быламеньше, чем аналогичная доля среди голосовавших, скажем заЯблоко или НДР. Естественно, из этого обстоятельства делалсявывод о том, что образованные люди не голосуют за компартию.
Но, вспоминая наши показатели, можно сказать, что, делаяэтот вывод, журналисты опирались только на сравнение величинемкостей детерминаций
(высшее образование) → (голосование за КПРФ),
(высшее образование) → (голосование за "Яблоко"),
(высшее образование) → (голосование за НДР),
т.е. на величины долей людей с высшим образованием средиголосовавших за разные партии. Однако обратимся к анализу интенсивностей тех же детерминаций. Оказывается, что за компартию в декабре проголосовало 1, 54 миллиона избирателей с высшим образованием, за "Яблоко" - 1, 43 миллиона, за НДР - 1, 3 миллиона ("Советская Россия", 21 марта 1996 года). Другимисловами, среди лиц с высшим образованием доля проголосовавшихза КПРФ (т.е. емкость первой детерминации), больше, чем доляпроголосовавших за "Яблоко" и НДР (т.е. емкости второй итретьей детерминации). Так за кого голосуют люди с высшим образованием? Предыдущий вывод вряд ли справедлив.
Вычисление интенсивности и емкости изучаемых детерминаций – основной элемент детерминационного анализа. При всей своей простоте этот подход заключает в себе глубокий смысл, поскольку требование обязательного вычисления названных показателей является своеобразной защитой от недосмотра социологов.
Кроме того, детерминационный анализ не сводится в анализу тех связей, которые мы назвали связями типа “альтернатива-альтернатива”. Он включает в себя целую систему алгоритмов, позволяющих повышать интенсивность и емкость рассматриваемых детерминаций, за счет учета значений множества признаков. Поясним подробнее, о чем здесь идет речь. Однако сначала отметим, что иногда в рамках детерминационного анализа используется терминология, несколько отличная от приведенной выше: интенсивность детерминации называется ее точностью, емкость – полнотой, сама детерминация – правилом "Если а, то b". "а" называется при этом объясняющим признаком, "b" – объясняемым. Замети, что Термин “признак” здесь используется в том смысле, который мы придавали словосочетанию “значение (альтернатива, градация) признака”. Надеемся, такое смешение терминов в данном параграфе не приведет к недоразумениям.
Предполагается, что в качестве объясняющего признака могут выступать конъюнкции и дизъюнкции любых значений рассматриваемых признаков-предикторов. При этом совокупность последних является “плавающей”. Все признаки-предикторы в таком случае называются объясняющими.
Процитируем некоторые положения из [Да-система…,1997. С. 160-161].
“Точность правила “Если а, то b” вычисляется по формуле:
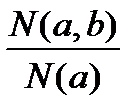 ,
,
где N (a,b) – количество объектов, обладающих одновременно объясняющим признаком а и объясняемым признаком b (количество подтверждений правила); N(a) – количество объектов, обладающих объясняющим признаком а безотносительно к любым другим признакам (количество применений правила). Точность измеряется от 0 до 1. Точность правила “Если а, то b” есть мера достаточности а для наличия b. Точность правила – это главный критерий его практической ценности. Наиболее ценятся правила, имеющие точность, близкую к 1.
Полнота правила – это мера его единственности. Она вычисляется по формуле:
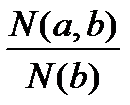 ,
,
Где N (b) – количество объектов, обладающих объясняемым признаком b безотносительно к любым другим признакам (объем объясняемого признака). Полнота изменяется от 0 до 1. Полнота правила “Если а, то b” есть мера необходимости а для наличия b. Полнота правила – это второй по значимости (после точности) критерий его практической ценности. Предельно точные правила ценятся тем выше, чем больше их полнота. Однако наличие высокой полноты не обязательно. Система точных правил, каждое из которых имеет небольшую полноту, может иметь чрезвычайную полезность для практики и науки, если ее суммарная полнота близка к 1”.
Пакет, реализующий детерминационный анализ [Да-система…,1997], позволяет эффективно подбирать конъюнкции объясняющих признаков для повышения точности правила, дизъюнкции – для повышения его полноты.
Например, предположим, что объясняемое положение – голосование за кандидата N. Допустим, что 40% мужчин проголосовали за N. Это значит, что точность правила “если мужчина, то голосует за N“ равна 0,4. Если мы рассмотрим мужчин с высшим образованием, точность детерминации может повыситься (а может, конечно, и не повыситься, и даже понизиться). Так, например, может оказаться, что за N проголосовали 80% мужчин с высшим образованием. Это будет означать, что, взяв конъюнкцию значения признака “пол”, означающее мужчину, и значения признака “образование”, отвечающее высшему образованию, мы повысили точность детерминации по сравнению с тем случаем, когда не учитывали образование респондента. Аналогичные рассуждения справедливы для полноты детерминации : ее тоже можно повышать с помощью удачного подбора объясняющих признаков.
Для сравнения ДА с другими алгоритмами, решающими сходные задачи, необходимо упомянуть еще два определения из [Да-система…,1997. С.161-162].
“Если какой-либо объясняющий признак убрать из правила, точность правила, вообще говоря, изменится. Величина этого изменения (с учетом знака) и есть, по определению, вклад объясняющего признака в точность. Рассмотрим правило “если а и b, то с". Вклад S (a) объясняющего признака в точность вычисляется по формуле
S(a) = (Точность правила "если а и b, то с“) – (точность правила “если b, то с").
Аналогично вычисляется вклад любого объясняющего признака в точность в любом заданном правиле." Совершенно аналогично определяется Вклад Q (a) объясняющего признака в полноту.
Заметим, что пакет программ, реализующий идеи детерминационного анализа на РС (ДА-система), пользуется большоя популярностью у социологов.
Более подробно мы не будем рассматривать ДА. Автор подхода, разработчики соответствующих программ для ЭВМ активно занимаются его пропагандой среди социологов. Однако в определенной мере мы вернемся к обсужденным положениям в п.п. 2.5.4 и 2.5.5, где попытаемся проанализировать ДА с точки зрения возможностей выявления обобщенных взаимодействий и сравнить его с методами поиска логических закономерностей.
Отметим только один факт, очень важный для нас в методологическом аспекте: автор детерминационного анализа развил его дальше, оригинальным образом обобщив положения аристотелевской силлогистики и построив стройную математическую теорию, отвечающую естественной логике социолога, “невооруженным глазом” анализирующего частотные таблицы [Чесноков, 1985]. Рождение этой теории является ярким примером того, как социологические потребности могут служить толчком для развития новых ветвей математики.
Анализ связей типа "группа альтернатив–группа альтернатив" и примыкающие к нему задачи
Итак, мы проанализировали суть связей типа "альтернатива× альтернатива", убедились в важности их изучения. Нетрудновидеть, что логика, сходная с использованной выше, приводит кмысли о необходимости изучения подобных связей для таких ситуаций, когда вместо отдельных альтернатив фигурируют их группы. Например, вместо задачи изучения связи между свойствами"быть учителем" и "читать Учительскую газету" мы можем поставить задачу проанализировать зависимость между свойствами"быть учителем, или врачом, или научным сотрудником, илииметь одну из т. н. творческих профессий" и "читать Литературную газету или журнал Новый Мир". Казалось бы, никаких проблемпри решении такой задачи не должно возникать. Нужно толькорассмотреть отвечающую нашим альтернативам подтаблицу исходной"большой" таблицы сопряженности и применить к ней уже знакомыенам способы измерения связей между двумя номинальными признаками.
Проблемы возникают в том случае, если мы не фиксируем заранее указанную подтаблицу, а ставим перед собой цель, например, найти такие подтаблицы исходной таблицы сопряженности,которые обладают свойствами, отличающими их от всей таблицы (либо от других подтаблиц). Например, такие, для которых тотили иной коэффициент связи больше (меньше), чем на всей таблице(на других подтаблицах). В качестве еще одной цели можетслужить изучение того, за счет каких подсвязей формируется наша "большая" связь. Можно считать целью изучение каких-то свойств, скажем, не учителей иврачей вместе (т.е. не такого множества респондентов, которое отвечает совокупности значений одного и того же признака -в данном случае - профессии), а, например, учителей старше 50лет, работающих в гимназиях (т.е. совокупности респондентов,отвечающей набору значений разных признаков - в данном случае- профессии, места работы и возраста). Возможны и другие повороты. Рассмотрим два класса методов, определяемых выбором цели.
Первый класс методов - группа альтернатив отвечает одному признаку.
Рассматриваемый класс определяется тем, что каждая из"групп альтернатив", означенных в названии нашего параграфа,состоит из значений одного признака (скажем, это разные наименования профессий, т.е. разные значения признака"профессия"). Исходная информация в таком случае представляетсобой таблицу сопряженности между двумя признаками, отвечающими нашим двум "группам альтернатив".
Здесь можно было бы, в свою очередь, говорить о возможности выделения двухподклассов задач.
Первый подкласс – математико-статистический. Речь идет о выяснении того, из каких компонент состоит величина "Хи-квадрат", вычисленная для рассматриваемой частотнойтаблицы, или, как мы будем говорить, о разложении этой величины на составные части, позволяющие определить, какой вклад внее осуществляют разные фрагменты таблицы сопряженности. Для решения соответствующих задач существуют строгие правила перенесения результатов с выборки на генеральную совокупность и т.д. Этот подкласс будет подробно рассмотрен нами в следующем параграфе.
Второй подкласс состоит из типичных задач анализа данных. Для них не разработан тот "антураж", котороготребуют строгие каноны математической статистики. Об этом подклассе скажем несколько слов здесь.
Будем полагать, чтонас не интересует разложение  , т.е. не интересует выяснениетого, из чего состоит эта величина, каков вклад в нее тех илииных фрагментов таблицы сопряженности. Зададимся более простойцелью: поиском в этой таблице таких ее подтаблиц, которые отличаются наиболее сильной связью (понимаемой в каком-нибудь изизвестных нам смыслов) между определяющими эти подтаблицы группами альтернатив. Ясно, что решение этой задачисводится к простому перебору всевозможных подтаблиц и вычислению отвечающих им показателей связи. Большой науки дляэтого не требуется. Мы не будем больше рассматривать эту задачу (и, стало быть второй подкласс методов), отметив, однако, ее важность для социолога.
, т.е. не интересует выяснениетого, из чего состоит эта величина, каков вклад в нее тех илииных фрагментов таблицы сопряженности. Зададимся более простойцелью: поиском в этой таблице таких ее подтаблиц, которые отличаются наиболее сильной связью (понимаемой в каком-нибудь изизвестных нам смыслов) между определяющими эти подтаблицы группами альтернатив. Ясно, что решение этой задачисводится к простому перебору всевозможных подтаблиц и вычислению отвечающих им показателей связи. Большой науки дляэтого не требуется. Мы не будем больше рассматривать эту задачу (и, стало быть второй подкласс методов), отметив, однако, ее важность для социолога.
Второй класс методов – группа альтернатив отвечает разным признакам.
Методы этого класса также относятся к типичным методаманализа данных, поскольку для них не разработан строгий математико-статистический подход. О них пойдет речь в п. 2.5.3. Мы увидим, что приведенное в заглавии п.2.5 название типа изучаемых связей естественным образом может быть обобщено: во многих реальных ситуациях вместозадач типа "(группа альтернатив)-(группа альтернатив)" имеетсмысл рассмотреть задачи типа "(группа альтернатив)-("поведение" респондентов)", где "поведение" может быть описано не только путем задания отвечающих рассматриваемым респондентам групп альтернатив, но и другими способами.
Вопросы для самопроверки
1. Какие возможные подходы знаете к изучению локальной связи?
2. Выход за пределы связей детерминационного анализа
3. Какие примыкающие задачи знаете к типу связи "группа альтернатив–группа альтернатив"?
Лекция 15.
Анализ связей типа "признак – группа признаков": номинальный регрессионный анализ (НРА).
Общая постановка задачи.
Мы подчеркивали,что в большинстве реальных задач исследователь не должен следовать ставшему традиционным ограничению круга используемыхматематических методов только известными коэффициентами парнойсвязи. При этом описывалось две совокупности факторов, обусловливающих необходимость перехода к другим методам.
Во-первых, имеет смысл "рассыпать" все рассматриваемыепризнаки на отдельные альтернативы и затем, "склеивая" их разными способами, искать такие сочетания значений исходных признаков, которые определяют те или иные связи, то или иное "поведение" респондентов (анализ фрагментов таблиц сопряженности,алгоритмы последовательных разбиений типа и т.д. ).
Во-вторых, имеет смысл объединять отдельные признаки другс другом, искать такие их сочетания, которые в каком-то смысле детерминируютдругие признаки и их сочетания (как мы увидим ниже, в регрессионном анализе речь пойдет о детерминации среднего уровня этих “других” признаков). К соответствующим рассмотрениям мы и перейдем в настоящем параграфе. Проанализируем тугруппу методов (или задач, мы говорили о том, что задачи длянас в определенном смысле отождествляются с методами), котораяпри классификации задач была символически обозначена нами какметоды типа "признак-(группа признаков)". Сюда относится регрессионный анализ, к рассмотрению которого мы и переходим.
| Рассыпание признаков на отдельные альтернативы |
| Объединение признаков друг с другом |
| Признак-признак |
Рис. 1. Схематичное выражение причин, обусловливающих необходимость перехода от традиционных коэффициентов парной связи к другим методам анализа связей
Сначала для простоты изложения рассмотрим случай, когда унас имеется только два признака – X и Y - и нас интересует зависимость между ними. Другими словами, сначала предположим,что наша "группа признаков" состоит из одного признака – X(потом перейдем к случаю, когда вместо одного X фигурируютнесколько признаков). Мы знаем, что о связи между признакамиговорит соответствующий коэффициент корреляции: чем ближе значение модуля этого коэффициента к 1, тем более сильна этасвязь, т.е. тем с большей уверенностью мы можем полагать, чтос ростом значений одного признака растут (если коэффициенткорреляции положителен) или убывают (если коэффициент корреляции отрицателен) значения другого (напомним, что коэффициент корреляции измеряет линейную связь междупеременными; отметим, однако, что приводимые рассуждения справедливы и длядругих коэффициентов связи, например, для корреляционного отношения, дающего возможность оценить криволинейную связь). Нопри этом мы совершенно не можем сказать о том, в какой степенивозрастет значение Y, если значение X увеличится, скажем, на1. А ситуации здесь могут быть весьма разными.
Приведем пример, рассмотрев зависимостьмежду производственным стажем человека и его зарплатой. Предположим, что мы имеем дело с двумя крайними ситуациями, отраженными на рисунках 21а и 21б. В обоих случаях соответствующие коэффициенты корреляции близки к 1 (обе совокупности
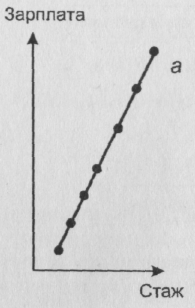
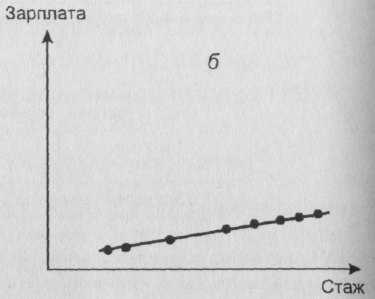
Рис. 2. Примеры сильных линейных связей, определяющих разный прогноз
точек-объектовлежат на прямых линиях, отвечающих нашей зависимости). На первом из них прямая идет резко вверх. Поэтому даже при небольшом увеличении X признак Y резко возрастет. В случае женаличия связи, изображенной на втором рисунке, прямая близка к горизонтали. Поэтому даже при значительномросте X значение Y почти не изменится. Другими словами, на основании наших двух картинок мы получим прогнозы совершенноразличного характера. И совершенно ясно, что этого никак нельзя узнать лишь на основе вычисления соответствующих коэффициентов корреляции.
Итак, для того, чтобы делать прогноз о том, как изменитсязначение Y при том или ином изменении значения X, нам желательнознать, как говорят, форму связи между этими переменными, т.е.желательно найти функцию вида Y = f (X). Подчеркнем, что отношение между X и Y несимметрично: речь идет именно о зависимости второй переменной от первой, именно о возможности прогнозазначения Y от X, а не наоборот.
В данном случае для обозначения X и Y используются те же термины, о которых шла речь в начале п. 2.5.3.1. Однако для той ситуации, когда речь идет о нахождении формы зависимости Y от X, употребляется еще несколько пар терминов: независимые переменные называют входными, экзогенными, внешними, а зависимая – выходной, эндогенной, внутренней. Представляется важным правильное понимание причин использования такой терминологии.
Поиск функции f предполагает разработку определенной модели связи между переменными, опирающуюся на априорные знания исследователя (так, ниже мы будем говорить в основном о линейной модели, о линейном регрессионном анализе). Найденная с помощью регрессионной техники зависимость – это тоже некоторая модель реальности - модель, в соответствии с которой и находятся значения Y на основе информациио значениях признака X.
Независимые признаки (X) потому и можно назвать независимыми, что они не зависят от этой модели. Эти признаки как бы поступают на ее “вход”, являются внешними по отношению к ней, берутся “со стороны”. Они определяют конкретный вид искомой зависимости, но не определяются ею. Прогнозируемые же значения зависимой переменной (Y) полностью определяются моделью (то, насколько они близки к реальности, зависит от качества модели), служат ее “выходом”, являются ее порождением. Они внутренне по отношению к ней.
Вопросы для самопроверки
1. Две совокупности факторов, обусловливающих необходимость перехода к другим методам.
2. Назовите сильные линейные связи, определяющих разный прогноз
[1] Gulliksen Н . Theory of Mental Tests. N. Y., 1950, р. 2.
Фокус-топ
Барлық сапалы әдістемелер ішінен соңғы кездері ең көп таралғаны фокус-топтар болып табылады. Бұл - зерттелетін объект жөнінде ақпарат алу мақсатындағы топтық пікір алысулар. Соңғысы оларды мақсаты белгілі бір көзқарастың жеңісі болып табылатын ғылыми немесе саяси пікір алысулардан өзгеше етеді.
Фокус-топтар құрамы (6-дан 12-ке дейінгі әрбір адам) зерттелетін жиынтық ішіндегі пікірлер, көңіл-күй, қажеттіліктер, талғамдар айырмашылығын барынша көрсету үшін іріктеп алынады (фокус-топты іріктеп алу рекруттеу деп аталады). Сонымен бірге, топтар ішінде жасы немесе білім деңгейі бойынша үлкен айырмашылықтарға жол берілмейді. Олай болмағанда, фокус-топтар әдісінде ақпарат алудың аса маңызды тәсілі болып табылатын топтық серпін жұмыс істемей қалуы мүмкін.
Фокус-топтар одан сайын алуан түрлі болуда және бүгіннің өзінде оларды бірнеше негіздер бойынша жіктеуге болады. Біз келесі жіктелімді ұсынамыз:
Құрамы бойынша
1-ші жіктелім (рекруттеудің күрделілігі бойынша):
| Қарапайым контингентпен (қатысушылар “бұқара” топтарын білдіреді) | Арнайы контингентпен (белгілі бір мамандық адамдары, белгілі бір қызмет пен сала қызметкерлері) | Қол жеткізу қиын немесе элита контингентпен |
2-ші жіктелім (қатысушылардың біркелкі немесе біркелкі емес деңгейі бойынша):
| Гомогенді (толығымен немесе көбінесе белгілі бір топ көрсетілген: жас өспірімдер, жастар, әйелдер, зейнеткерлер және т.б.) | Гетерогенді (әр түрлі әлеуметтік-демографиялық және әлеуметтік-кәсіби топтар көрсетілген) |
3-ші жіктелім (өзіндік немесе топтық /корпоративтік көзқарастары мен қызығушылықтарының көрсетілуі бойынша:
| Өзін-өзі білдіретін қатысушылар | Ұйымдарды білдіретін қатысушылар |
Рекруттеу әдісі бойынша:
| “Көшеден”, кездейсоқ рекруттелгендер | Белгілі бір өлшемдер бойынша (мысалы, кәсі-бі, кәсіпорынның көлемі немесе меншік түрі) рекруттелгендер | Арнайы нұсқаулар бойынша рекруттелгендер (белгілі бір ком-пания қызметкерлері, қандай да бір оқиғаға қатысушылар) |
Мақсатты нұсқаулар мен өткізілу техникасы бойынша:
| Қоршаған орта проблемасын талқылау | Оқиғаларды, фактілерді талқылау | Өзіндік көңіл-күйлерді, әсер-лерді, өзінің өмір стилін талқылау | Тауар үлгілері мен жарнамалық өнімдерді тестілеу |
Фокус-топтың жүргізушісі модератор деп аталады. Модератордың жұмысы жоғары біліктілікті қажет етеді, көбінесе фокус-топты кәсіби психологтар немесе әлеуметтанушылар жүргізеді. Модераторда терең сұхбатта гайд деп аталатын пікір алысудың жалпы жоспары болады. Бірақ, терең сұхбатқа қарағанда, фокус-топта гайд одан да төмен нақтыланған. Әдетте, ол компьютермен терілген мәтіннің 2 бетін алады. Фокус-топтың өзі 2-2,5 сағат жүргізіледі. Бұл модератордың суырып салма қабілетінің үлкен рөлін көрсетеді. Модератор фокус-топтың қымбат уақытын тек қана зерттеу мақсаттары үшін пайдалануды қамтамасыз етіп, қызықты пікірталас тудырып, әрбір қатысушыдан барынша көбірек пайдалы ақпаратты “сығып алып”, гайдтың барлық сұрақтары бойынша “пікірлер таратуды” белгілеуі тиіс. Әсіресе кез келген топта таныс емес адамдар арасындағы әңгімеде кездесетін “лидерді басу” міндетті түрде қиындыққа әкеледі. Модератор тең шамада, пікір алысу үшін барлық қатысушыларды әңгімеге тартуы тиіс, өйткені олардың әрқайсысы ақпараттың бірегей қайнар көзі болып табылады.
Фокус-топтар аудио немесе бейнепленкаға жазылады, жазбалар негізінде арнайы әдістемен түсіндіру (транскриптер), резюме мен есептер дайындалады.
Бақылау
Әлеуметтану бақылауы өзінің әр түрінде зерттеушіге сандық, сол сияқты сапалық, кейде екеуінің бір жиынтығында ақпарат береді. Ақпарат жинау процестер мен құбылыстарды визуалды және есту арқылы қабылдауға негізделген. Бақылаудың ерекше белгісі оны, әдетте, басқа әдістермен бір жиынтықта пайдалану болып табылады.
Бақылауды, әдетте, рәсімнің формализмге негізделу деңгейі, бақылаушының орны, ұйымдастыру жағдайлары, жүргізудің жүйелілігі бойынша жіктейді. Бірінші негіздеме бойынша бақылау стандартты және стандартты емес болып бөлінеді. Стандартты бақылауды арнайы жоспар бойынша зерттелетін объектінің алдын ала анықталған элементтерінің тіркелуін білдіреді. Стандартты емес әдістемеде мұндай жоспар жоқ, зерттеу мақсаттары үшін маңызды жайлар бақылау процесінің өзінде айқындалады.
Бақылаушының зерттеу объектісіне қатысты жағдайына орай бақылау енгізілмеген және енгізілген (қатысушы) болуы мүмкін. Енгізілмеген бақылау кезінде зерттеуші зерттелетін объектіден тыс тұрады. Ол оқиға барысына енгізілмейді және сұрақтар қоймайды. Енгізілген бақылауда зерттеуші бақыланушылармен тікелей байланыста болады, олардың іс-әрекетіне қатысады. Енгізілген бақылау өз кезегінде жасырын (жариялы емес, құпиялы) және ашық болып бөлінеді.
Ұйымдастыру жағдайы бойынша далалық және лабораториялық бақылау бөлініп шығады. Бірінші жағдайда мәліметтер жинау кәдімгі жағдайда, шынайы өмір жағдайында, екіншісінде - жасанды түрде құрылған және бақылаушының бақылауындағы жағдайда жүзеге асырылады.
Жүйелілігі бойынша бақылау жүйелі, эпизодтық және кездейсоқ болуы мүмкін.
Бақылау әдісінің қолдану аясы айтарлықтай кең - маркетингтен бастап ғылым әлеуметтануына дейін – кіші топтарды зерттеуден бұқаралық сана мен мінез-құлықты зерттеуге дейін болады.
Дәріс 3. Математиканың әлеуметтанудағы қолданудың негізгі бағыттары
Әлеуметтану мен математиканың арақатынасы мәселелері
Веяние нового времени, бэконовские идеи опытного знания, развитие Галилеем эмпирического естествознания оказали влияние на развитие социальных наук, способствуя проникновению в них количественных методов. В середине XVII в. появляется работа В. Петти «Политическая арифметика», в которой он пишет: «...вместо того чтобы употреблять слова только в сравнительной и превосходной степени и прибегать к умозрительным аргументам, я вступил на путь выражения своих мнений на языке чисел, весов и мер (я уже стремился давно пойти по этому пути, чтобы показать пример политической арифметики), употребляя только аргументы, идущие от чувственного опыта, и рассматривая только причины, имеющие видимое основание в природе. Те же, которые зависят от непостоянства умов, мнений, желаний и страстей отдельных людей, я оставляю другим. Замечания или положения, выражаемые посредством числа, весов и мер, на которых я основывал нижеследующие рассуждения, являются или верными .или не явно ложными».
Как известно, К. Маркс назвал В. Петти «изобретателем статистики». Однако как самостоятельная наука статистика сформировалась много позднее, а у В. Петти и в последующих работах этого направления статистика (или то, что мы называем сейчас статистикой) выступала как всеобщая социальная эмпирическая наука. Анализ становления статистики чрезвычайно важен, поскольку ее стиль мышления, метод (в частности, идея показателя) глубоко проникли в экономику, позднее — в социологию и психологию.
В начальном этапе развития статистики определились два самостоятельных и отчасти противоположных направления — политическая арифметика в Англии, идущая от Петти и Граунта, и так называемая университетская статистика в Германии, связанная с именами Конринга и Ахенвалля. Направление Петти — числовой анализ: основная идея — вместо слов числа и пропорции. В. Петти ищет показатели, характеризующие население Лондона, и приходит к определению числа жителей этого города тремя способами: 1) по числу домов, семейств и душ, живущих в каждом из них; 2) по числу смертных случаев в благоприятные для здоровья годы и по отношению числа живущих к числу умерших; 3) по числу умерших от чумы в годы эпидемий и по отношению этого числа к числу тех, кто избежал смерти
Линия Конринга — поиск классификационных систем, систематизации категорий, характеризующих общество. Он исходит из четырех аристотелевых причин. Общество как организм имеет цель, и это конечная причина, по Аристотелю и по Конрингу. Аристотелева материальная причина, по Конрингу, связана со знанием о людях и товарах. Причина формальная—это законы страны. Причина действующая определяет конкретные пути управления обществом. Каждая из причин-категорий в свою очередь детализируется. Например, действующая причина содержит в себе субъекты управления и средства управления. Первые—это правители сами по себе; вторых подразделяют на одушевленные и неодушевленные. Главный представитель последних — деньги.
Во всех областях социологического исследования математические методы играют огромную роль — это относится как к капиталистическим, так и к социалистическим странам. В Советском Союзе большую известность получили работы А. Г. Аганбегяна, Ф. М. Бородкина, Ю. Н. Гаврильца, Т. И. Заславской, В. Н. Шубкина и других ученых. В других странах социалистического лагеря известны работы И. Краземан (ГДР), Ж. Старкова (НРБ), С. Шосткевича (ПНР), И. Матея (СРР) я др.
Арсенал применяемых в социальных науках математических средств весьма обширен и многообразен — различные методы математической статистики, теория игр, теория информации, аппарат теории устойчивости, теория марковских цепей, линейное программирование, факторный анализ, корреляционный анализ, теория графов, матричная алгебра и многое другое.
Вся история конкретных социальных исследований в нашей стране была связана со все более широким и более специализированным использованием математики. В первых конкретных социальных исследованиях 50-х — начала 60-х годов были взяты на вооружение простейшие математические и статистические средства — метод средних чисел, метод аналитических группировок, индексный метод анализа, т.е. методы так называемой дескриптивной статистики. В это же время был остро поставлен вопрос о репрезентативности исследований.
По мере развития конкретных исследований применялись все более точные математические методы анализа данных и выборки. Оперирование с большими массивами социальной информации привело к проблеме использования вычислительной техники — счетно-перфорационных и электронно-вычислительных машин.
Социологи столкнулись с необходимостью измерения качественных социальных переменных и моделирования социальных процессов и явлений. Все это вызвало большой интерес к обсуждению методологических проблем применения математики в социологии.
Работы, посвященные исследованию методологических проблем применения математики в марксистско-ленинской социологии, охватывают огромный круг вопросов, который в свою очередь требует определенной классификации. Не претендуя на бесспорность, можно выделить следующие направления среди методологических проблем применения математических методов в социологии, придерживаясь в основном хронологического порядка их постановки: во-первых, роль статистических закономерностей в конкретных социологических исследованиях; во-вторых, возможности и перспективы применения математики в марксистско-ленинской социологии; в-третьих, работы по определению основных типов задач, которые могут быть решены в социологии математическими средствами.
На страницах многих советских специальных журналов в 50-е годы шла острая дискуссия о роли познания статистических нединамических закономерностей окружающего мира. Эта дискуссия первоначально была вызвана трудностями в материалистической интерпретации квантовой механики, а затем перешла в область применения статистических закономерностей к анализу социальных явлений.
В ходе этой дискуссии сложились две точки зрения. Согласно первом статистика — это исключительно социально-экономическая наука, использующая некоторые математические методы; вторая точка зрения утверждает, что статистика — универсальная наука, изучающая массовые случайные процессы безотносительно к их специфике.
В конце концов дискуссия по проблемам статистики пришла к формулировке двух весьма важных выводов: во-первых, объективности статистических закономерностей в сфере социальной жизни общества и необходимости использования общей и математической статистики при проведении конкретных социологических исследований; во-вторых, необходимости применения математических методов к анализу социальных закономерностей.
Массовые процессы в природе и обществе различны. Те стороны массовых социальных процессов, которые получают количественное выражение, и представляют собой предмет статистики. Однако при этом неправомерно отождествление индивидуальных и случайных различий при анализе социальных данных. Необходимо строго отделять индивидуальные статистические различия от случайных, выявлять содержательную специфику случайного и статистического в социальной действительности.
Неправомерно подходить к экономическим и социальным явлениям с мерками, заимствованными из области изучения явления природы. Статистическая совокупность, с которой имеет дело социолог, существенно отличается от совокупности, с которой имеет дело натуралист. Социолог манипулирует со сводными данными: суммами, средними и т.д. Для индивидуальных событий общественной жизни отсутствуют главные признаки событий стохастической среды — независимость и равновозможность. Можно применять вариационные показатели для социальных (неслучайных) распределений. Существует мнение, что оценка результатов не может быть дана на базе вероятностных, сто-
Дәріс 4. Өлшеу сапасы. Әлеуметтанулық индекстер және шкалалар
Жиынтық мәліметтер дереккөздері
Әлеуметтанулық өлшеу. Өлшеу деңгейлері. Өлшеу сенімділігі мен валидтілігі.
Шкала түсінігі. Шкалаларды құрылымдау
Проблема измерения в науке нового времени является одной из центральных и в методологическом, и практическом отношениях. Если применение математики во многих областях естествознания уже вышло за рамки самой проблемы измерения (хотя в последней есть много нерешенных вопросов), то среди математических проблем социальных наук и, в частности, социологии вопросы измерения пока еще остаются центральными. И в последнее время они привлекают все большее и большее внимание.
Практика измерения восходит в своих началах к истокам науки, однако логические основания измерения не изучались вплоть до конца XIX -начала ХХ в., когда Гельмгольц изложил основные идеи репрезентационной теории измерения, а Гельдер развил аксиоматику измерения экстенсивных величин.
Интуитивная ясность в понимании сущности измерения не покидает нас, как только возникает речь об измерении. Однако более тщательный анализ проблем измерения сталкивается со значительными трудностями.
Мы говорим, что диаметр подшипника мы измеряем, а диаметр Луны, Солнца мы определяем, вычисляем, находим. Когда ставим отметку па экзамене, то измеряем знания студента и одновременно оцениваем их. Одно ли это и то же? Не измеряют ведь дерево вообще, а измеряют его высоту, поперечник у основания, т.е. измеряют не предмет, а его свойства и опять же не все свойства, а только те, которые можно измерить. То свойство, что дерево хвойное или лиственное, не измеряется вообще.
С развитием психологии и социологии в основном начиная с 30-х годов ХХ в. появилась острая необходимость в сравнении, сопоставлении величин аддитивности которые не удовлетворяют условиям. Это привело к созданию новой теории измерений. Идея ее была выдвинута крупнейшим современным психологом С. Стивенсом на рубеже 30-40-х годов. По Стивенсу, измерение возможно прежде всего потому, «что существует изоморфизм между свойствами числовых рядов и эмпирическими операциями, которые мы можем производить с объектами».
Измерение понимается как процесс соотнесения эмпирической системы с некоторой числовой системой. Из-за отсутствия единиц измерения таких величин, как удовлетворенность жизнью, национальное чувство и т.п., возник вопрос о специфике числовой системы, которая соотносится с эмпирической системой. Стивенс первоначально выдвинул четыре типа таких числовых систем, которые обусловили четыре соответствующие шкалы (или уровни) измерения: шкала наименований (номинальная), порядка (ординальная), интервалов (интервальная) и отношений.
Каждая шкала характеризуется соответствующими числовыми свойствами. Если производится измерение по определенной шкале, то это означает, что осуществляется изоморфизм между числовой системой шкалы и исследуемыми величинами. Сам Стивенс дал разделение шкал на основе тех математических преобразований, которые допускаются каждой шкалой.
Шкала наименований допускает операцию равенства-неравенства, т.е. ее числовая система обладает весьма слабыми свойствами. Эта шкала (или измерение по ней) дает простую классификацию объектов, например нумерацию игроков в футбольной команде. С числами, приписанными игрокам, мы не можем оперировать, как с числами в арифметике, а именно два игрока первого номера нам нe дадут игрока второго номера и т.п. Эти числа только отличают игроков друг от друга. Шкала порядка допускает операции равенства - неравенства и больше-меньше. Она представляет собой ранжирование по признаку (например, ряд металлов в химии). Примером такой шкалы может быть «измерение» критериев отношения к труду:
"Какие из указанных ниже суждений выражают ваше мнение?
1. Хороша любая работа, если она хорошо оплачивается.
2. Заработок главное, но важен и смысл работы, ее общественная значимость.
3. Нельзя забывать о заработке, но главное - смысл, содержание работы.
4. Хороша та работа, где ты приносишь больше пользы".
Шкала интервалов допускает операции равенства-неравенства, больше-меньше и равенства-неравенства интервалов, позволяя тем самым ввести единицу измерения. Шкала отношений допускает операции равенства-неравенства, больше-меньше, равенство интервалов и равенство отношений и тем самым реализует все арифметические операции. По этим последним двум шкалам производятся все физические измерения.
Различие шкал можно проиллюстрировать на nростом примере. Предположим, мы выявляем удовлетворенность работой. Если мы можем подразделить людей только на удовлетворенных и неудовлетворенных работой, то тем самым имеем номинальную шкалу удовлетворенности работой. Если можно было бы установить, насколько и во сколько раз удовлетворенность одних больше удовлетворенности других, то получили бы интервальную шкалу, а также шкалу отношений удовлетворенности работой. Данные, представленные (измеренные) по номинальной и ординарной шкалам, принято именовать качественными, а измеренные по шкалам интервальной и отношений количественными, поскольку первые две не допускают арифметических операций, а вторые — допускают В каждой шкале применяются строго установленные статистические методы.
Таблица 1
Шкалы измерения *
| Шкала | Основные эм-прирические операции | Математическая групповая структура | Допустимая статистика | Типичные примеры |
| Наименований (номинальная) | Установление равенства | Группа перестановок | Число случаев, мода, корреляция качественных переменных | Нумерация игроков футбольной команды |
| Порядковая (ординальная) | Установление отношений (больше-меньше) | Изотоническая группа | Медиана, ранговая корреляция | Ранжирование лиц по признаку |
| Интервальная | Установление равенства интервалов | Группа линейных преобразований | Среднее арифметическое, корреляция количественных переменных | Температура по Цельсию или Фаренгейту, энергия, календарные даты; баллы тестирования |
| Отношений | Установление равенства отношений | Группа подобия | Все операции математической статистики | Длина, вес, сопротивление, шкала высоты звука, шкала громкости звука |
| * Схема с небольшими изменениями заимствована из книги: Стивенс С. Экспериментальная психология, т. 1, с. 52 | ||||
Кумбс, развивая идеи С. Стивенса, предложил эквивалентный в математическом отношении подход к различению шкал посредством различения характера арифметических операций. Соответственно, каждая шкала характеризуется своей системой аксиом, которые и определяют числовые свойства шкалы. Стивенс не ставил целью дать строгую логическую формулировку шкал посредством аксиом. Формулировка аксиом для порядковой шкалы и шкалы отношений была дана Э. Найгелем. Кумбс предлагал рассматривать шкалы как математические конструкции, для которых важны два момента: объек ты и расстояния между объектами. По его мнению, можно провести классификацию шкал Стивенса как для элементов, так и для расстояний между ними.
Дәріс 5-6. Айнымалылар түрлері және олардың статистикалық сипаттамалары
1. Номиналды айнымалылар
2. Реттік айнымалылар
3. Интервалды айнымалылар
Номинальные переменные представляют минимальную информацию об изучаемом явлении. Они дают лишь набор дискретных категорий, позволяющих разграничить разные объекты. Номинальное измерение – этопростое наименование объектов в соответствии с заранее заданной схемой классификации. Например, пол - мужской и женский; национальность - русские, украинцы, немцы, англичане и т.д. Это измерение не сообщает, насколько характеристика «национальность» свойственна разным людям.Номинальное измерение дает возможность объединить объекты в классы,
где цифры просто обозначают категории классификации безотносительно к порядку их расположения. Измерение средней тенденции происходит путем исчисления моды. Мода - это наиболее часто встречающееся значение признака. Если в распределении признака наблюдается одно значение моды, то распределение называется унимодальным, если несколько, – полимодальным. Когда две категории обладают равным количеством случаев (наибольших), то распределение будет бимодальное.
Для того чтобы определить, насколько типична мода для нашего распределения, вычисляем дисперсию.
Значение коэффициента вариации колеблется между нулем, когда все случаи принимают одно и то же значение, и единицей, когда каждый случай имеет свое значение. Чем меньше коэффициент вариации, тем типичнее мода. В случае полимодального распределения для расчета величины ν выбирается одно из модальных значений, вокруг которого производятся вычисления.
При использовании номинальных переменных следует основываться на взаимоисключающих и исчерпывающихся категориях. Это означает, что невозможно отнести один объект к более чем одной категории, но при этом каждый объект обязательно должен быть отнесен к какой-либо категории.
Порядковые переменные
Порядковые переменные дают возможность не только категоризировать, но и упорядочивать, или ранжировать значения. При порядковых измерениях можно присваивать каждому объекту число, которое обозначает как именно данный объект связан с другими в терминах количества того конкретного свойства, которым он характеризуется. При этом возникает возможность расположить объекты по порядку, в зависимости от количества свойства, которое их характеризует.
Например, понятие «социальный класс» имеет три порядковых уровня: низший, средний, высший. В порядковых измерениях должно быть не менее трех классов, при этом расстояние между классами не устанавливается, известно только, что они образуют некую последовательность. От классов легко перейти к числам, если условиться считать: низший класс получает ранг 1; средний - ранг 2; и так далее или наоборот. Чем больше классов в шкале, тем больше возможностей для математической обработки полученных данных.
Средняя тенденция порядковых переменных определяется медианой.
Медиана – это значение признака в упорядоченном ряду, до и после которого находится равное количество признаков. Вычисление медианы требует отсчитать с обоих концов распределения признака равное количество до тех пор, пока мы не дойдем до серединного, который и определяет значение медианы.
Если в ряду значений признаков четное число членов (2k), медиана равна среднему арифметическому из двух серединных значении признака. При нечетном числе членов (2k+1) медианным будет значение признака (k+1) объекта. Например, для 100 это 50 и 51. Если они принадлежат одному значению признака, то оно и будет медианой, если они принадлежат разным значениям, то медианой будет среднее среди них или оба.
Пример. В выборке из 10 человек респонденты проранжированы по стажу работы на данном предприятии:
Ранг 1 2 3 4 5 6 7 8 9 10
Стаж 15 13 10 9 7 6 5 4 3 1
Серединные ранги 5 и 6, поэтому медиана равна (7+6)/2=6,5лет. Таким образом, установили, что 50% рабочих имеют стаж меньше 6,5 лет, и 50% рабочих - больше 6,5 лет.
Измерение дисперсии для порядковых переменных состоит в вычислении квантильного ранга. Квантильный ранг – это мера положения внутри распределения, означающая, какая часть значений из всей совокупности, считая от меньшего значения вверх, находится ниже
рассмотренной точки.
Среди квантилей выделяют:
персентиль, деление совокупности на сто равных частей так, что первый персентиль - такое значение в этой совокупности (считая от меньшего значения вверх), ниже которого находится 1% всех случаев;
дециль - деление совокупности на десятые доли;
квинтиль - деление совокупности на пятые доли;
квартиль - деление совокупности на четверти.
Любой из указанных квантилей может быть использован для определения дисперсии порядковой величины вокруг медианы, хотя чаще используют децильные и квинтильные ранги.
Интервальные переменные
Интервальные переменные представляют наиболее полную количественную информацию об измеряемых данных. Исследователь получает возможность не только классифицировать и упорядочивать объекты, но и устанавливать, насколько большим или меньшим количеством измеряемого свойства по сравнению с другими объектами они характеризуются.
Интервальные измерения основаны на представлении о существовании некоторой стандартной единицы измеряемого свойства.
Значения, полученные по результатам интервальных измерений, могут быть подвержены любым арифметическим операциям.
Главной единицей для интервальных данных является среднее арифметическое значение, которое определяет среднюю тенденцию. Среднее арифметическое значение есть частное от деления суммы всех значений признака на их число.
Дәріс 7. Мәліметтерді жинау мен талдаудағы индекстер
Жанама индекстер
Логикалық квадрат. Логикалық үшбұрыш.
Жиынтықты бағалау шкаласы. Уақыт бюджетіндегі, мемлекеттік статистикадағы индекстер
Дәріс 8. Өлшеудің кейбір ерекше амалдары
Семинар/практикалық/ зертханалық сабақтары 7.
Луи Тернстоун шкаласы.
Эмори Богардус шкаласы.
Луи Гутманн шкалограммды талдауы
Дәріс 9. Психологиялық тесттер және социологиялық шкалалар
Впервые идею тестов выдвинул английский биолог Ф. Гальтон. Ему же принадлежит заслуга создания техники изучения индивидуальных различий на основе использования статистического метода. Гальтон искал способ математического описания тех закономерностей, которым подчиняются индивидуальные различия. В качестве метода он применил вариационную статистику.
В своих исканиях он опирался на работы А. Кетле – одного из создателей современной статистики. В своей работе «Социальная физика» (1835) Кетле показал, что формулы теории вероятности позволяют обнаружить факт подчинения поведения людей некоторым закономерностям. При анализе статистического материала он получил постоянные величины, дающие количественное описание таких актов человеческого поведения, как вступление в брак или самоубийство.
В интерпретации полученных данных Кетле исходил из идеи «среднего человека» – некоего идеала, отклонение которого изображается нормальным законом распределения. Если средняя является постоянной, то за ней должна стоять некая реальность, что позволяет предсказывать явления на основе статистических законов. Чтобы найти эти законы, безнадежно изучать каждого индивида в отдельности. Следует изучать поведение большой массы людей, используя метод вариационной статистики.
Давая статистический анализ биографических данных, Гальтон предлагал использовать законы Кетле для распределения человеческих способностей. Он считал, что существует средняя величина умственных способностей, так же как и средний рост.
Испытания, проводившиеся в антропологической лаборатории, организованной Гальтоном на Международной выставке в Лондоне в 1884 г., он назвал психологическими тестами. В широкий оборот этот термин вошел после выхода в свет в 1890 г. статьи его ученика – американского психолога Дж. М. Кеттелла – «Психологические тесты и измерения». В этой статье Кеттелл выдвинул требование статистического подхода – применения серии тестов к большому числу индивидов, полагая, что психология не сможет стать такой же точной наукой, как науки физические, если не будет базироваться на эксперименте и измерении.
Определенный сдвиг в этом направлении, по его мнению, может быть сделан путем применения серии психологических тестов к большому числу индивидов.
Разработанные Гальтоном приемы вариационной статистики вооружили психологию важным методическим средством. Среди них наиболее перспективным оказался метод исчисления коэффициента корреляции между переменными. Этот метод, усовершенствованный английским математиком К. Пирсоном и другими последователями Гальтона, внес в психологическую науку ценные математические методики, в результате использования которых возник в дальнейшем факторный анализ (работы Ч. Спирмена, Э. Л. Торндайка, Л. Терстона и др.). Постепенно совершенствовались методы статистической обработки результатов, контроля их надежности, обоснованности.
Начиная с 1905 г. французский психолог А. Бине в сотрудничестве с врачом Т. Симоном выполнили серию экспериментов по изучению умственных способностей людей различных возрастов. Проведенные на многих испытуемых (и тем самым подчиненные статистическим критериям), эти эксперименты превратились в тесты для определения уровня умственного развития. Индивидуальные различия испытывались уже не сами по себе, а в их отношении к возрастному ряду. Так возникла метрическая шкала интеллекта Бине – Симона, которая явилась первым стандартизированным тестом не только по унификации заданий и процедур их выполнения, но и по оценке полученных показателей. Это побудило ввести понятие умственного возраста – МА (Mental Age) в отличие от хронологического возраста – СА (Chronological Age). Их несовпадение считалось показателем либо умственной отсталости (МА ниже СА), либо одаренности (МА выше СА).
В 1912 г. немецкий психолог В. Штерн ввел понятие «коэффициент интеллекта» Intelligence Quotient – IQ как показатель темпа умственного развития, свойственного данному ребенку:
 Коэффициент указывает на опережение или отставание умственного возраста относительно хронологического. Л. Терман, профессор психологии Стэнфордского университета в США, вместе со своими сотрудниками дважды (в 1916 и 1937 rr.) осуществил переработку шкалы Бине – Симона. Так возникла известная шкала Стэнфорд – Бине.
Коэффициент указывает на опережение или отставание умственного возраста относительно хронологического. Л. Терман, профессор психологии Стэнфордского университета в США, вместе со своими сотрудниками дважды (в 1916 и 1937 rr.) осуществил переработку шкалы Бине – Симона. Так возникла известная шкала Стэнфорд – Бине.
В связи с тем, что интеллект, как полагали, есть нечто увеличивающееся вместе с возрастом ребенка, и так как согласно всем предварительным стандартным оценкам чем старше ребенок, тем лучше его характеристики почти в любом единичном умственном тесте, то вполне естественно возраст был воспринят в качестве психологической меры интеллекта.
Кроме индивидуальных тестов, подобных тестам Бине, применяющих возраст в качестве измеряющей шкалы, существуют также групповые тесты, которые применяются более широко и используют в качестве единиц измерения тестовые вопросы. Тестовый балл – это взвешенное и невзвешенное число вопросов, на которые правильно ответил индивид с некоторой поправкой на случайность правильного ответа, если это необходимо. Тесты обычно состоят из большого числа разнородных вопросов, меняющихся по трудности от очень легких до очень трудных.
В настоящее время теория тестов представляет собой хорошо разработанную дисциплину, включающую в себя целый ряд проблем. При составлении тестов, анализе и интерпретации результатов учитываются пять основных требований, по Галликсену[1]. 1) составление и отбор тестовых вопросов; 2) присвоение балла каждому индивиду; 3) определение точности (надежности или ошибки измерения) тестовых баллов; 4) определение предсказующего значения тестовых баллов (обоснованности или ошибки оценивании); 5) сравнение этих результатов с результатами, полученными при использовании других тестов или других групп испытуемых.
Нас в первую очередь будут интересовать вопросы, связанные с математической стороной техники тестирования.
Наиболее общим видом теста является тест, в котором каждый вопрос представляет определенную задачу. Балл – это число «правильных» ответов в ограниченное время. Вопросы могут быть неодинаковыми по трудности или же концентрироваться на одном уровне трудности. В последнем случае одни испытуемые имеют более высокую вероятность ответов, чем другие и, следовательно, более высокий уровень способности. Если вопросы имеют разные уровни трудности, то некоторые испытуемые могут ответить на более трудные вопросы и тем самым получить более высокий балл. Временной предел является еще одним источником разброса баллов, так как разные испытуемые работают с разной скоростью.
Самый обычный тип тестового балла – суммарный балл. Он основан на суммировании ответов определенной категории – правильных или неправильных.
Если мы предложим каждому из испытуемых тест из т вопросов, то результаты сможем представить в матрице вопросных баллов, в которой каждый столбец представляет соответствующий вопрос i, а каждая строка соответствующего испытуемого j.
| Вопросы | |||||||||||||
| a | b | c | i | N | 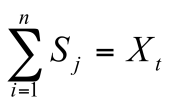
| ||||||||
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| 2 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 4 |
| 3 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 |
| 4 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 5 |
| 5 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| . | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 6 |
| . | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 7 |
| J | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 9 |
| . | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 11 |
| N | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 12 |
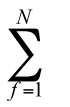
| 10 | 9 | 9 | 7 | 6 | 6 | 5 | 4 | 3 | 3 | 2 | 1 | 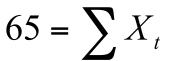
|
| 1,0 | 0,9 | 0,9 | 0,7 | 0,6 | 0,6 | 0,5 | 0,4 | 0,3 | 0,3 | 0,2 | 0,1 | 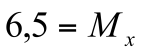
| |
Каждый испытуемый пытается ответить на каждый вопрос, и поэтому каждый вопросный балл 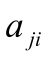 будет либо 0, либо 1. Сумма вопросных баллов в строке – это общий балл испытуемого, сумма вопросных баллов в столбце – это число испытуемых, правильно ответивших на вопрос этого столбца. Таким образом, матрица является источником информации как относительно вопросов, так и относительно испытуемых. Поделив каждую сумму вопросных баллов в столбцах на N, мы получим долю испытуемых
будет либо 0, либо 1. Сумма вопросных баллов в строке – это общий балл испытуемого, сумма вопросных баллов в столбце – это число испытуемых, правильно ответивших на вопрос этого столбца. Таким образом, матрица является источником информации как относительно вопросов, так и относительно испытуемых. Поделив каждую сумму вопросных баллов в столбцах на N, мы получим долю испытуемых 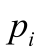 , правильно ответивших на соответствующий вопрос.
, правильно ответивших на соответствующий вопрос.
Доля тех, кто правильно ответил на определенный вопрос, является простым способом описания трудности этого вопроса. Фактически это есть средняя баллов, и чем она ниже, тем труднее вопрос.
Дәріс 10.
Статистика және әлеуметтанудағы мәліметтерді өңдеу
Слово «статистика» часто ассоциируется со словом «математика», и это пугает студентов, связывающих это понятие со сложными формулами, требующими высокого уровня абстрагирования.
Однако, как говорит Мак-Коннелл, статистика — это прежде всего способ мышления, и для ее применения нужно лишь иметь немного здравого смысла и знать основы математики. В нашей повседневной жизни мы, сами о том не догадываясь, постоянно занимаемся статистикой. Хотим ли мы спланировать бюджет, рассчитать потребление бензина автомашиной, оценить усилия, которые потребуются для усвоения какого-то курса, с учетом полученных до сих пор отметок, предусмотреть вероятность хорошей и плохой погоды по метеорологической сводке или вообще оценить, как повлияет то или иное событие на наше личное или совместное будущее, — нам постоянно приходится отбирать, классифицировать и упорядочивать информацию, связывать ее с другими данными так, чтобы можно было сделать выводы, позволяющие принять верное решение.
Все эти виды деятельности мало отличаются от тех операций, которые лежат в основе научного исследования и состоят в синтезе данных, полученных на различных группах объектов в том или ином эксперименте, в их сравнении с целью выяснить черты различия между ними, в их сопоставлении с целью выявить показатели, изменяющиеся в одном направлении, и, наконец, в предсказании определенных фактов на основании тех выводов, к которым приводят полученные результаты. Именно в этом заключается цель статистики в науках вообще, особенно в гуманитарных. В последних нет ничего абсолютно достоверного, и без статистики выводы в большинстве случаев были бы чисто интуитивными и не могли бы составлять солидную основу для интерпретации данных, полученных в других исследованиях.
Для того чтобы оценить огромные преимущества, которые может дать статистика, мы попробуем проследить за ходом расшифровки и обработки данных, полученных в эксперименте. Тем самым, исходя из конкретных результатов и тех вопросов, которые они ставят перед исследователем, мы сможем разобраться в различных методиках и несложных способах их применения. Однако, перед тем как приступить к этой работе, нам будет полезно рассмотреть в самых общих чертах три главных раздела статистики.
1. Описательная статистика, как следует из названия, позволяет описывать, подытоживать и воспроизводить в виде таблиц или графиков
данные того или иного распределения, вычислять среднее для данного распределения и его размах и дисперсию.
2. Задача индуктивной статистики — проверка того, можно ли распространить результаты, полученные на данной выборке, на всю популяцию, из которой взята эта выборка. Иными словами, правила этого раздела статистики позволяют выяснить, до какой степени можно путем индукции обобщить на большее число объектов ту или иную закономерность, обнаруженную при изучении их ограниченной группы в ходе какого-либо наблюдения или эксперимента. Таким образом, при помощи индуктивной статистики делают какие-то выводы и обобщения, исходя из данных, полученных при изучении выборки.
3. Наконец, измерение корреляции позволяет узнать, насколько связаны между собой две переменные, с тем чтобы можно было предсказывать возможные значения одной из них, если мы знаем другую.
Существуют две разновидности статистических методов или тестов, позволяющих делать обобщение или вычислять степень корреляции. Первая разновидность — это наиболее широко применяемые параметрические методы, в которых используются такие параметры, как среднее значение или дисперсия данных. Вторая разновидность — это непараметрические методы, оказывающие неоценимую услугу в том случае, когда исследователь имеет дело с очень малыми выборками или с качественными данными; эти методы очень просты с точки зрения как расчетов, так и применения. Когда мы познакомимся с различными способами описания данных и перейдем к их статистическому анализу, мы рассмотрим обе эти разновидности.
Как уже говорилось, для того чтобы попытаться разобраться в этих различных областях статистики, мы попробуем ответить на те вопросы, которые возникают в связи с результатами того или иного исследования. В качестве примера мы возьмем один эксперимент, а именно — изучение влияния потребления марихуаны на глазодвигательную координацию и на время реакции. Методика, используемая в этом гипотетическом эксперименте, а также результаты, которые мы могли бы в нем получить, представлены ниже.
При желании вы можете заменить какие-то конкретные детали этого эксперимента на другие — например, потребление марихуаны на потребление алкоголя или лишение сна, — или, что еще лучше, подставить вместо этих гипотетических данных те, которые вы действительно получили в вашем собственном исследовании. В любом случае вам придется принять «правила нашей игры» и выполнять те расчеты, которые здесь от вас потребуются; только при этом условии до вас «дойдет» существо предмета, если это уже не случилось с вами раньше.
Важное примечание. В разделах, посвященных описательной и индуктивной статистике, мы будем рассматривать только те данные эксперимента, которые имеют отношение к зависимой переменной «поражаемые мишени». Что касается такого показателя, как время реакции, то мы обратимся к нему только в разделе о вычислении корреляции. Однако само собой разумеется, что уже с самого начала значения этого показателя надо обрабатывать так же, как и переменную «поражаемые мишени». Мы предоставляем читателю заняться этим самостоятельно с помощью карандаша и бумаги.
Некоторые основные понятия. Популяция и выборка
Одна из задач статистики состоит в том, чтобы анализировать данные, полученные на части популяции, с целью сделать выводы относительно популяции в целом.
Популяцияв статистике не обязательно означает какую-либо группу людей или естественное сообщество; этот термин относится ко всем существам или предметам, образующим общую изучаемую совокупность, будь то атомы или студенты, посещающие то или иное кафе.
Выборка — этонебольшое количество элементов, отобранных с помощью научных методов так, чтобы она была репрезентативной, т.е. отражала популяцию в целом.
(В отечественной литературе более распространены термины соответственно «генеральная совокупность» и «выборочная совокупность». — Прим. перев.)
Данные и их разновидности
Данные в статистике — это основные элементы, подлежащие анализу. Данными могут быть какие-то количественные результаты, свойства, присущие определенным членам популяции, место в той или иной последовательности — в общем любая информация, которая может быть классифицирована или разбита на категории с целью обработки.
Не следует смешивать «данные» с теми «значениями», которые эти данные могут принимать. Для того чтобы всегда различать их, Шатийон (Chatillon, 1977) рекомендует запомнить следующую фразу: «Данные часто принимают одни и те же значения» (так, если мы возьмем, например, шесть данных — 8, 13, 10, 8, 10 и 5, то они принимают лишь четыре разных значения — 5, 8, 10 и 13).
Построение распределения — это разделение первичных данных, полученных на выборке, на классы или категории с целью получить обобщенную упорядоченную картину, позволяющую их анализировать.
Существуют три типа данных:
1. Количественные данные, получаемые при измерениях (например, данные о весе, размерах, температуре, времени, результатах тестирования и т. п.). Их можно распределить по шкале с равными интервалами.
2. Порядковые данные, соответствующие местам этих элементов в последовательности, полученной при их расположении в возрастающем порядке (1-й, ..., 7-й, ..., 100-й, ...; А, Б, В. ...).
3. Качественные данные, представляющие собой какие-то свойства элементов выборки или популяции. Их нельзя измерить, и единственной их количественной оценкой служит частота встречаемости (число лиц с голубыми или с зелеными глазами, курильщиков и не курильщиков, утомленных и отдохнувших, сильных и слабых и т.п.).
Из всех этих типов данных только количественные данные можно анализировать с помощью методов, в основе которых лежат параметры (такие, например, как средняя арифметическая). Но даже к количественным данным такие методы можно применить лишь в том случае, если число этих данных достаточно, чтобы проявилось нормальное распределение. Итак, для использования параметрических методов в принципе необходимы три условия: данные должны быть количественными, их число должно быть достаточным, а их распределение — нормальным. Во всех остальных случаях всегда рекомендуется использовать непараметрические методы.
Вопросы для самопроверки
1. Перечислите основные значения понятия «анализ данных».
2. Каковы уровни анализа эмпирических данных?
3. Что такое «социологические данные»? Каковы их виды?
4. Назовите основные стадии социологического исследования.
5. Что представляет собою предмет курса «Анализ данных в социологии»?
Лекция 11. Суреттеу статистикасы
Описательная статистика позволяет обобщать первичные результаты, полученные при наблюдении или в эксперименте. Процедуры здесь сводятся к группировке данных по их значениям, построению распределения их частот, выявлению центральных тенденций распределения (например, средней арифметической) и, наконец, к оценке разброса данных по отношению к найденной центральной тенденции.
Дата: 2019-03-05, просмотров: 615.