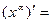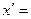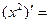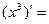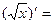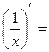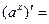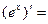Ен .01. МАТЕМАТИКА
Специальность
27.02.07 Управление качеством продукции, процессов и услуг (по отраслям)
Квалификация выпускника
техник - технолог
Чебоксары, 2018
Фонд оценочных средств (далее – ФОС) по учебной дисциплине (далее – УД) ЕН.01. Математика программы подготовки специалистов среднего звена (ППССЗ) по специальности 27.02.07 Управление качеством продукции, процессов и услуг базового уровня разработан на основе Федерального государственного образовательного стандарта (далее – ФГОС) по специальности 27.02.07 Управление качеством продукции, процессов и услуг в соответствии с рабочей программой учебной дисциплины ЕН.01. Математика
Разработчик:
Леонтьева Т.Ю., преподаватель МЦК-ЧЭМК Минобразования Чувашии
СОГЛАСОВАНО
Председатель ЦК специальности (М) Л.Г. Андреева
Содержание
1. Область применения ФОС по учебной дисциплине ЕН.01. Математика
2. Программа текущего контроля успеваемости студентов
3. ФОС для проведения текущего контроля
4. Программа промежуточной аттестации студентов
5. ФОС для промежуточной аттестации
1. Область применения ФОС по учебной дисциплине ЕН.01. Математика
ФОС предназначен для проверки результатов освоения учебной дисциплины основной профессиональной образовательной программы (далее ОПОП) по специальности 15.02.15 Технология металлообрабатывающего производства.
ФОС позволяет оценивать следующие результаты освоения УД:
1. Элементы профессиональных компетенций (ПК) и общих компетенций (ОК):
Таблица 1
| Профессиональные и общие компетенции |
| ПК 1.3. Разрабатывать технологическую документацию по обработке заготовок на основе конструкторской документации в рамках своей компетенции в соответствии с нормативными требованиями, в том числе с использованием систем автоматизированного проектирования |
| ПК 1.4. Осуществлять выполнение расчётов параметров механической обработки и аддитивного производства в соответствии с принятым технологическим процессом согласно нормативным требованиям, в том числе с использованием систем автоматизированного проектирования |
| ПК 1.5. Осуществлять подбор конструктивного исполнения инструмента, материалов режущей части инструмента, технологических приспособлений и оборудования в соответствии с выбранным технологическим решением, в том числе с использованием систем автоматизированного проектирования |
| ПК 1.6. Оформлять маршрутные и операционные технологические карты для изготовления деталей на механических участках машиностроительных производств, в том числе с использованием систем автоматизированного проектирования |
| ПК 1.7. Осуществлять разработку и применение управляющих программ для металлорежущего или аддитивного оборудования в целях реализации принятой технологии изготовления деталей на механических участках машиностроительных производств, в том числе с использованием систем автоматизированного проектирования |
| ПК 1.10. Разрабатывать планировки участков механических цехов машиностроительных производств в соответствии с производственными задачами, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.3. Разрабатывать технологическую документацию по сборке узлов или изделий на основе конструкторской документации в рамках своей компетенции в соответствии с нормативными требованиями, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.4. Осуществлять выполнение расчётов параметров процесса сборки узлов или изделий в соответствии с принятым технологическим процессом согласно нормативным требованиям, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.5. Осуществлять подбор конструктивного исполнения сборочного инструмента, материалов исполнительных элементов инструмента, приспособлений и оборудования в соответствии с выбранным технологическим решением, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.6. Оформлять маршрутные и операционные технологические карты для сборки узлов или изделий на сборочных участках машиностроительных производств, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.7. Осуществлять разработку управляющих программ для автоматизированного сборочного оборудования в целях реализации принятой технологии сборки узлов или изделий на сборочных участках машиностроительных производств, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.10. Разрабатывать планировки участков сборочных цехов машиностроительных производств в соответствии с производственными задачами, в том числе с использованием систем автоматизированного проектирования |
| ПК 3.1. Осуществлять диагностику неисправностей и отказов систем металлорежущего и аддитивного производственного оборудования в рамках своей компетенции для выбора методов и способов их устранения |
| ПК 3.4. Организовывать ресурсное обеспечение работ по наладке металлорежущего и аддитивного оборудования в соответствии с производственными задачами, в том числе с использованием SCADA систем |
| ПК 3.5. Контролировать качество работ по наладке, подналадке и техническому обслуживанию металлорежущего и аддитивного оборудования и соблюдение норм охраны труда и бережливого производства, в том числе с использованием SCADA систем |
| ПК 4.1. Осуществлять диагностику неисправностей и отказов систем сборочного производственного оборудования в рамках своей компетенции для выбора методов и способов их устранения |
| ПК 4.4. Организовывать ресурсное обеспечение работ по наладке сборочного оборудования в соответствии с производственными задачами, в том числе с использованием SCADA систем |
| ПК 4.5. Контролировать качество работ по наладке, подналадке и техническому обслуживанию сборочного оборудования и соблюдение норм охраны труда и бережливого производства, в том числе с использованием SCADA систем |
| ПК 5.2. Организовывать определение потребностей в материальных ресурсах, формирование и оформление их заказа с целью материально-технического обеспечения деятельности структурного подразделения |
| ОК 01. Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам |
| ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности |
| ОК 09. Использовать информационные технологии в профессиональной деятельности |
| ОК 10. Пользоваться профессиональной документацией на государственном и иностранном языках |
2. Знания и умения:
Таблица 2
| Знания: |
| основные математические методы решения прикладных задач |
| основы дифференциального и интегрального исчислений |
| основные методы и понятия математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики |
| роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности |
| Умения: |
| анализировать сложные функции и строить их графики |
| выполнять действия над комплексными числами |
| вычислять значения геометрических величин |
| производить действия над матрицами и определителями |
| решать задачи на вычисление вероятности с использованием элементов комбинаторики |
| решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений |
| решать системы линейных уравнений различными методами |
Перечень рекомендуемых учебных изданий,
ОЦЕНОЧНОЕ СРЕДСТВО № 1
ЗАДАНИЕ ДЛЯ СОЧИНЕНИЯ
ОЦЕНОЧНОЕ СРЕДСТВО № 2
Тема 1.1. Теория пределов
Справочный материал
В процессе проведения сборочных работ различных видов техники, обработки деталей применяются контрольно-измерительные приборы (КИП). В паспортах КИП при описании датчиков указываются диапазоны измерений. Например, от 50 до 350 мА. Поскольку результаты измерений однозначно определяются входными данными измерений, то эти результаты могут быть рассмотрены как некоторые функции, которые будут ограниченными, то есть имеющими верхний и нижний пределы. Например, если шкала датчика КИП маркирована от 30 до 150 м3/ч, то нижний предел измерения равен 30 м3/ч, а верхний 150 м3/ч.
Вариант 1
1. Вычислить предел функции:
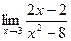 .
.
2. Вычислить предел функции:
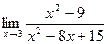 .
.
3. Вычислить предел функции:
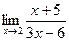 .
.
4. Вычислить предел функции:
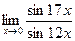 .
.
5. Вычислить предел функции:
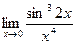 .
.
6. Вычислить предел функции:
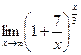 .
.
Вариант 2
1. Вычислить предел функции:
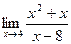 .
.
2. Вычислить предел функции:
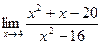 .
.
3. Вычислить предел функции:
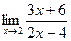 .
.
4. Вычислить предел функции:
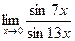 .
.
5. Вычислить предел функции:
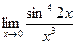 .
.
6. Вычислить предел функции:
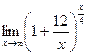 .
.
Вариант 3
1. Вычислить предел функции:
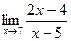 .
.
2. Вычислить предел функции:
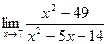 .
.
3. Вычислить предел функции:
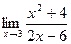 .
.
4. Вычислить предел функции:
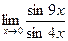 .
.
5. Вычислить предел функции:
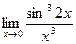 .
.
6. Вычислить предел функции:
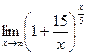 .
.
Вариант 4
1. Вычислить предел функции:
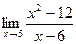 .
.
2. Вычислить предел функции:
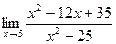 .
.
3. Вычислить предел функции:
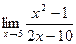 .
.
4. Вычислить предел функции:
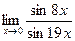 .
.
5. Вычислить предел функции:
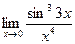 .
.
6. Вычислить предел функции:
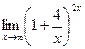 .
.
Вариант 5
1. Вычислить предел функции:
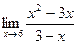 .
.
2. Вычислить предел функции:
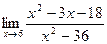 .
.
3. Вычислить предел функции:
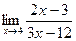 .
.
4. Вычислить предел функции:
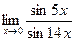 .
.
5. Вычислить предел функции:
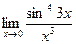 .
.
6. Вычислить предел функции:
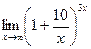 .
.
Вариант 6
1. Вычислить предел функции:
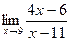 .
.
2. Вычислить предел функции:
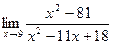 .
.
3. Вычислить предел функции:
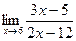 .
.
4. Вычислить предел функции:
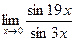 .
.
5. Вычислить предел функции:
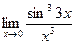 .
.
6. Вычислить предел функции:
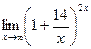 .
.
Пакет преподавателя
Вариант 1
1. 4.
2. 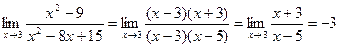 .
.
3. 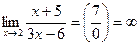 .
.
4. 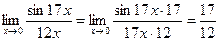 .
.
5. 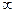 .
.
6. 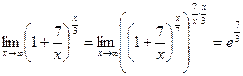 .
.
Вариант 2
1. –5.
2. 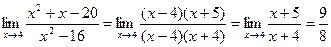 .
.
3. 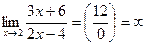 .
.
2. 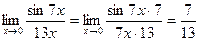 .
.
3. 0.
4. 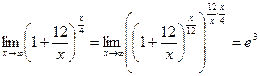 .
.
Вариант 3
1. 5.
2. 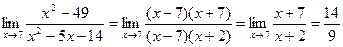 .
.
3. 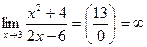 .
.
2. 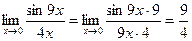 .
.
3. 8.
4. 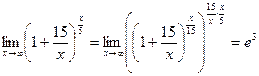 .
.
Вариант 4
1. –13.
2. 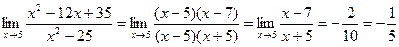 .
.
3. 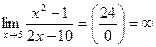 .
.
2. 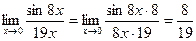 .
.
3. 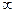 .
.
4. 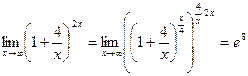 .
.
Вариант 5
1. –6.
2. 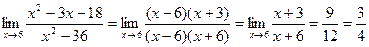 .
.
3. 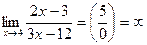 .
.
4. 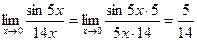 .
.
5. 0.
6. 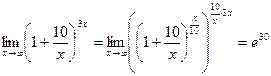 .
.
Вариант 6
1. –15.
2. 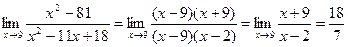 .
.
3. 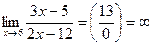 .
.
1. 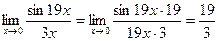 .
.
2. 27.
3. 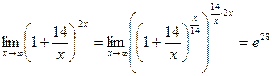 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 3
Тема 1.1. Теория пределов
Справочный материал
В процессе проведения сборочных работ различных видов техники, обработки деталей применяются контрольно-измерительные приборы (КИП). Основной качественной характеристикой любого датчика КИП является погрешность измерения контролируемого параметра. Погрешность измерения прибора это величина расхождения между тем, что показал (измерил) датчик КИП и тем, что есть на самом деле. С точки зрения математики абсолютная погрешность может быть рассмотрена как приращение аргумента: разница между измеренным значением величины и ее действительным значением.
Приращение – это изменение величины, например, начальное значение напряжения U1=220В, конечное значение U2=120В; изменение напряжения (или дельта напряжения) будет равно ΔU=U2–U1=220В–120В=100В.
Вариант 1
1. Исследовать функцию 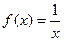 на непрерывность в точке
на непрерывность в точке 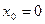 .
.
2. Вычислить приращение данной функции, если ее аргумент x получает приращение 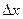 :
:
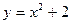 ,
, 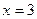 ,
, 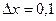 .
.
Вариант 2
1. Исследовать функцию 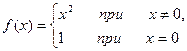 на непрерывность в точке
на непрерывность в точке 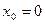 .
.
2. Вычислить приращение данной функции, если ее аргумент x получает приращение 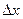 :
:
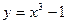 ,
, 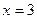 ,
, 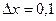 .
.
Вариант 3
1. Исследовать функцию 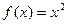 на непрерывность в точке
на непрерывность в точке 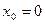 .
.
2. Вычислить приращение данной функции, если ее аргумент x получает приращение 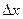 :
:
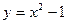 ,
, 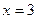 ,
, 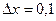 .
.
Пакет преподавателя
Вариант 1
1. Решение.
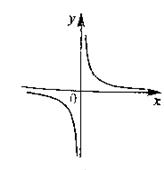
Проверим условия из определения.
1) 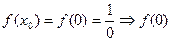 не существует, т. е. функция
не существует, т. е. функция 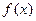 неопределенна в точке
неопределенна в точке 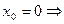 функция
функция 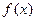 не является непрерывной в точке
не является непрерывной в точке 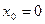 .
.
Ответ. Не является непрерывной.
Вариант 2
1. Решение.
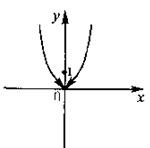
Проверим условия из определения.
1) 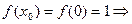 функция
функция 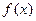 определенна в точке
определенна в точке 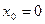 .
.
2) 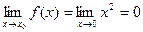 . Функция
. Функция 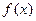 имеет конечный предел при
имеет конечный предел при 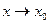 .
.
3) 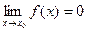 ,
, 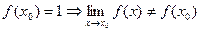 . Предел функции при
. Предел функции при 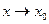 не равен значению функции в этой точке.
не равен значению функции в этой точке.
Ответ. Не является непрерывной.
Вариант 3
1. Решение.
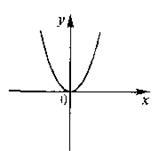
Проверим условия из определения.
1) 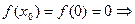 функция
функция 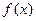 определенна в точке
определенна в точке 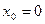 .
.
2) 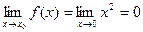 . Функция
. Функция 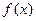 имеет конечный предел при
имеет конечный предел при 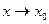 .
.
3) 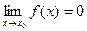 ,
, 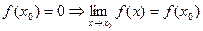 . Предел функции при
. Предел функции при 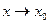 равен значению функции в этой точке.
равен значению функции в этой точке.
Ответ. Непрерывна.
ОЦЕНОЧНОЕ СРЕДСТВО № 4
Перечень вопросов и задач
- Дать определение производной функции.
- В чем заключается геометрический смысл производной?
- В чем заключается физический смысл производной?
- Что такое дифференциал функции?
- Какая функция называется сложной?
- Что такое вторая производная и производные высших порядков?
- В чем заключается физический смысл второй производной?
- Сформулировать правила дифференцирования и записать производные основных элементарных функций и производную сложной функции:
| 1о. | 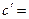
| 8о. | 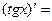
|
| 2о. |
В частности, | 9о. | 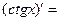
|
| 10о. | 
| ||
| 11о. | 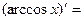
| ||
| 12о. | 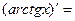
| ||
| 13о. | 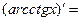
| ||
| ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ | |||
| 14о. | 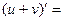
| ||
| 3о. | 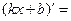
| 15о. | 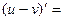
|
| 4о. |
В частности, | 16о. | 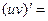
|
| 17о. | 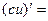
| ||
| 5о. | 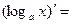 В частности,
В частности, 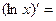
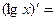
| 18о. | 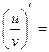 В частности,
В частности, 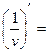
|
| 6о. | 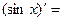
| ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ | |
| 7о. | 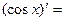
| 19о. | 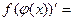
|
- Найти производные следующих функций:
а) 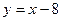 ;
;
б) 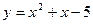 ;
;
в) 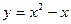 ;
;
г) 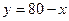 .
.
- Найти производные функций и вычислить их значения в точках
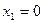 и
и 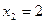 :
:
а) 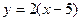 ;
;
б) 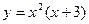 ;
;
в) 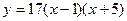 ;
;
г) 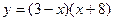 ;
;
д) 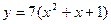 ;
;
е) 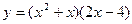 .
.
-
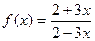 . Найти
. Найти 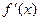 ,
, 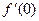 ,
, 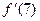 ,
, 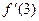 .
. -
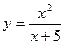 . Найти
. Найти 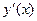 ,
, 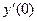 ,
, 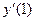 .
. - Найти производную следующей функции:
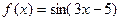 .
.
- Найти производную следующей функции:
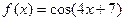 .
.
- Найти производную следующей функции:
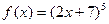 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 5
Пакет преподавателя
| № вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| правильный ответ | а | в | б | а | а | в | в | б | а | а |
ОЦЕНОЧНОЕ СРЕДСТВО № 6
кейс-задание
Справочный материал
Как воздух математика нужна,
Одной отваги мало.
Расчёты! Залп! И цель поражена
Могучими ударами металла.
И воину припомнилось на миг,
Как школьником мечтал в часы ученья
О подвиге, о шквалах огневых,
О яростном порыве наступленья.
Но строг учитель был, и каждый раз
Он обрывал мальчишку резковато:
«Мечтать довольно! Повтори рассказ
О свойствах круга и углах квадрата!»
И воином любовь сбережена
К учителю далёкому, седому.
Как воздух математика нужна
Сегодня офицеру молодому!
При освоении больших скоростей авиация столкнулась с внезапным разрушением самолетов из-за вибрации особого рода – флаттера. На определенных режимах работы моторов в конструкциях возникли самовозбуждающиеся вибрации. Флаттер (от англ. flutter – трепыхаться, бить крыльями) – явление аэроупругости, одна из разновидностей вибраций – незатухающих упругих колебаний частей летательного аппарата, возникающих в полёте при скорости полёта, достигшей некоторого определённого значения – критической скорости флаттера Vкр. Эти колебания порождаются аэродинамическими воздействиями и относятся к автоколебаниям. Флаттер среди автоколебаний и вообще среди многочисленных видов вибраций, которым подвержены летательные аппараты, представляет особую опасность, заключающуюся в том, что возникающие при этих интенсивных колебаниях динамические напряжения в конструкции летательного аппарата могут быстро (иногда в течение несколько секунд) достигнуть разрушающих значений, результатом чего является разрушение летательного аппарата в полёте. Поэтому возникновение флаттера любой формы недопустимо.
Опасности подстерегали скоростные машины и на земле. При взлете или посадке самолета его колеса вдруг начинали вилять из стороны в сторону. Это явление, названное шимми, нередко вызывало катастрофы самолётов на аэродромах. Шимми (англ. shimmy) – автоколебания колёс шасси летательного аппарата, возникающие вследствие неустойчивости процесса их прямолинейного качения. Явление шимми во многом аналогично явлению флаттера. Шимми проявляется как интенсивные поперечные колебания колёс шасси при движении летательного аппарата по земле с относительно высокой скоростью (обычно более 100 км/ч).
Флаттер и шимми стали препятствием на пути создания скоростной авиации. Развитие скоростной авиации во всём мире сопровождалось большим числом катастроф и аварий в результате их возникновения. Впервые с их массовыми случаями столкнулись в 30-е гг. ΧΧ в. (в период стремительного роста скоростей), после чего началось интенсивное изучение этих явлений и отыскание способов их предупреждения. Статистика лётных происшествий насчитывает много случаев, связанных с флаттером и шимми.
Выдающийся советский математик Мстислав Всеволодович Келдыш и возглавляемый им коллектив учёных исследовали причины флаттера и шимми. Созданная учёными математическая теория этих опасных явлений позволила авиационной науке своевременно защитить конструкции скоростных самолётов от появления таких вибраций. Однако ещё не всё об этих опасных вибрациях известно; с созданием новых схем летательных аппаратов проявляются их новые аспекты, требующие пристального и глубокого внимания ученых-математиков.
Вибрация – механические колебания. В теории колебаний рассматриваются всевозможные колебания, абстрагируясь от их физической природы (можно строить теорию, используя понятие материальной точки, а не детали самолета). И для этого используется аппарат дифференциального исчисления. Например, гармонические колебания – это такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса: 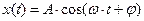 .
.
Задача для самостоятельного решения
Колебательное движение точки описывается уравнением 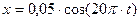 . Найти координату, скорость и ускорение спустя 1/60 секунды после момента начала колебаний.
. Найти координату, скорость и ускорение спустя 1/60 секунды после момента начала колебаний.
Пакет преподавателя
Решение задачи

При работе над кейсом применяется групповая технология обучения, в рамках которой с помощью наблюдения за деятельностью студентов можно зафиксировать следующие поведенческие признаки:
- планирование студентами своей деятельности в рамках заданной технологии;
- обучение студентами других членов микрогрупп и всей группы рациональным приемам по организации деятельности для эффективного выполнения коллективного проекта;
- распределение студентами объема работы среди участников коллективного проекта;
- преодоление студентами кризисов взаимодействия совместно с членами группы.
Данные признаки нашли отражение в критериях оценки выполнения кейс-задания.
Кроме того, при наблюдении за выполнением студентами данного задания можно оценить, в какой мере каждый студент осознает и восполняет недостаток информации, освоенных умений и усвоенных знаний в процессе реализации деятельности, определяет стратегию решения проблемы, разбивает поставленную цель на задачи, проявляет патриотизм, анализирует полученные профессиональные знания применительно к военным технологиям.
ОЦЕНОЧНОЕ СРЕДСТВО № 7
Справочный материал
Для обработки заготовок на универсальных станках и станках с ЧПУ необходимо сообщить режущему инструменту и заготовке определенный, как правило достаточно сложный, комплекс согласованных друг с другом движений. Эти движения подразделяются на основные (рабочие) и вспомогательные. Основные движения – это движения исполнительных органов станка, благодаря которым непосредственно осуществляется процесс снятия стружки режущим инструментом с обрабатываемой заготовки. К основным движениям относятся главное движение и движение подач. Главное движение обусловливает скорость процесса резания. Оно определяется как прямолинейное поступательное или вращательное движение заготовки, происходящее с наибольшей скоростью в процессе резания. При токарной обработке таким движением является вращательное движение заготовки. При фрезерной обработке, а также при сверлильной и расточной работах – вращательное движение режущего инструмента. Движение подач обусловливает величину, скорость и характер взаимного перемещения инструмента и заготовки, предназначенного для того, чтобы распространить отделение срезаемого слоя материала на всю обрабатываемую поверхность заготовки. Движение подач может быть прямолинейным или по дуге, непрерывным или прерывистым, и оно всегда имеет скорость меньшую, чем главное движение. При токарной обработке движением подач являются перемещения суппорта с режущим инструментом. При фрезерной обработке и расточной работе – перемещения рабочего стола с заготовкой, при сверлильной работе – перемещения пиноли и т.п. Вспомогательные движения – это движения исполнительных органов станка и приспособлений, необходимые для подготовки процесса резания. К ним относятся движения, связанные с транспортировкой и закреплением заготовки, подводом и отводом режущего инструмента и т. п.
Любое движение может быть описано с помощью дифференциального и интегрального исчисления.
Вариант 1
1. Найти производную функции 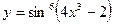 .
.
2. Найти производную третьего порядка функции 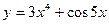 .
.
3. Написать уравнение касательной к графику функции 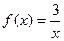 в точке с абсциссой
в точке с абсциссой 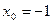 ,
, 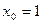 .
.
4. Материальная точка движется по закону 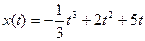 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 2
1. Найти производную функции 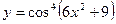 .
.
2. Найти производную третьего порядка функции 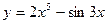 .
.
3. Написать уравнение касательной к графику функции 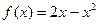 в точке с абсциссой
в точке с абсциссой 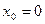 ,
, 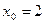 .
.
4. Материальная точка движется по закону 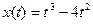 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 3
1. Найти производную функции 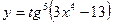 .
.
2. Найти производную третьего порядка функции 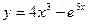 .
.
3. Написать уравнение касательной к графику функции 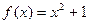 в точке с абсциссой
в точке с абсциссой 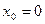 ,
, 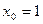 .
.
4. Материальная точка движется по закону 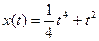 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 4
1. Найти производную функции 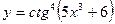 .
.
2. Найти производную третьего порядка функции 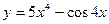 .
.
3. Написать уравнение касательной к графику функции 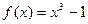 в точке с абсциссой
в точке с абсциссой 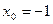 ,
, 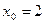 .
.
4. Материальная точка движется по закону 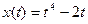 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 5
1. Найти производную функции 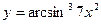 .
.
2. Найти производную третьего порядка функции 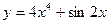 .
.
3. Написать уравнение касательной к графику функции 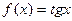 в точке с абсциссой
в точке с абсциссой 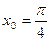 ,
, 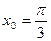 .
.
4. Материальная точка движется по закону 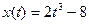 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 6
1. Найти производную функции 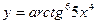 .
.
2. Найти производную третьего порядка функции 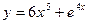 .
.
3. Написать уравнение касательной к графику функции 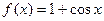 в точке с абсциссой
в точке с абсциссой 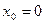 ,
, 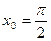 .
.
4. Материальная точка движется по закону 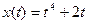 . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Пакет преподавателя
Вариант 1
1. 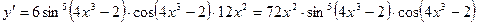 .
.
Вариант 2
1. 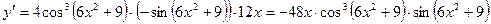 .
.
Вариант 3
1. 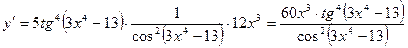 .
.
Вариант 4
1. 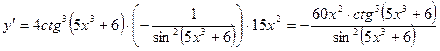 .
.
Вариант 5
1. 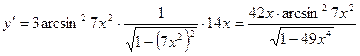 .
.
Вариант 6
1. 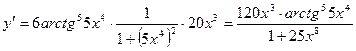 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 8
Справочный материал
По распространенному убеждению, в жизни человека чередуются черные и белые полосы. Если сегодня ты огорчен, тебя преследуют неудачи, самочувствие все ухудшается, то вскоре надо ждать какого-то просветления. Конечно, не всегда это так. Но некоторая закономерность все равно есть.
А чем же эти белые и черные полосы определяются? Одним словом, от чего на самом деле зависит наше состояние и самочувствие?
Огромную роль в жизни человека играют циклы. Цикличность – одно из самых главных свойств всего мироздания. Существуют циклы суточные, сезонные, годовые. Циклично движение солнца и планет солнечной системы. И вот около ста лет назад появилась теория «трех биоритмов».
Физический биоритм регулирует физическую активность, силу, скорость, координацию, выносливость. Примеры этого мы наблюдаем достаточно часто в повседневной жизни. Всякому футбольному болельщику известна сакраментальная фраза спортивных комментаторов, что у такого-то футболиста сегодня не идет игра. Как правило, это связано как раз с тем, в какой фазе физического биоритма находится данный игрок.
Эмоциональный биоритм влияет на накал эмоций, на остроту восприятия, на чувствительность. Все, наверное, замечали, что один и тот же человек иногда может проявить чуткость и понимание, а в какой-то другой ситуации остаться абсолютно равнодушным.
Интеллектуальный биоритм отвечает за умственные способности, ясность мышления, остроту памяти. С перепадами такого биоритма очень хорошо знакомы люди научного труда. Бывает, что в какие-то дни любая задача, даже самая сложная, решается на удивление легко. А случается, что на выполнении простейшей работы невозможно сосредоточиться и крайне трудно довести ее до конца.
Биоритм можно представить в виде синусоиды с периодом, равным циклу. В момент рождения человека синусоиды находятся в нуле (начале системы координат). Ритмичность физического цикла составляет 23 дня, психический цикл длится 28 дней, а интеллектуальный биоритм составляет 33 дня. По оси абсцисс располагаются даты, а переменная х означает прожитые человеком дни. Нижняя точка синусоиды называется минимумом, а высшая – максимумом. И если минимум обычно характеризуется упадком сил, вялостью, отсутствием положительных эмоций, то уж максимум позволяет человеку полностью раскрыть себя и все свои возможности. В каждом цикле два минимума и два максимума. Особенно важны минимумы. Может наступить такой момент, когда несколько минимумов совпадут. Вот это и называется в словесном обиходе «черными днями», когда все буквально валится из рук. Если какие-то даты пересекаются двумя или более синусоидами – это и есть критические дни. В некоторых странах людей опасных профессий (диспетчеров, пилотов, водителей) не допускают к работе, им дают выходной. Но если совпадут несколько максимумов, вы можете просто свернуть горы.
Математически физический цикл описывается функцией 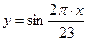 , эмоциональному циклу соответствует функция
, эмоциональному циклу соответствует функция 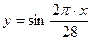 , а описание интеллектуального цикла соответствует формуле
, а описание интеллектуального цикла соответствует формуле 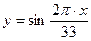 .
.
Вариант 1
1. Исследовать функцию и построить ее график: 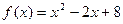 .
.
2. Построить график физического биоритма. Определить точки максимума. Выполнить анализ полученных результатов.
Вариант 2
1. Исследовать функцию и построить ее график: 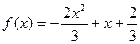 .
.
2. Построить график физического биоритма. Определить точки минимума. Выполнить анализ полученных результатов.
Вариант 3
1. Исследовать функцию и построить ее график: 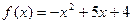 .
.
2. Построить график эмоционального биоритма. Определить точки максимума. Выполнить анализ полученных результатов.
Вариант 4
1. Исследовать функцию и построить ее график: 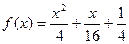 .
.
2. Построить график эмоционального биоритма. Определить точки минимума. Выполнить анализ полученных результатов.
Вариант 5
1. Исследовать функцию и построить ее график: 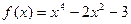 .
.
2. Построить график интеллектуального биоритма. Определить точки максимума. Выполнить анализ полученных результатов.
Вариант 6
1. Исследовать функцию и построить ее график: 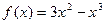 .
.
2. Построить график интеллектуального биоритма. Определить точки минимума. Выполнить анализ полученных результатов.
ОЦЕНОЧНОЕ СРЕДСТВО № 9
Перечень вопросов и задач
- Дать определение первообразной.
- Дать определение неопределенного интеграла.
- Перечислить основные свойства неопределенного интеграла (записать).
- Записать табличные интегралы:
1о. 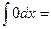 2о.
2о. 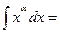 В частности,
В частности, 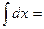 3о.
3о. 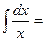 4о.
4о. 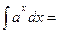 В частности,
В частности, 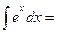 5о.
5о. 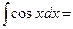 6о.
6о. 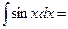
| 7о. 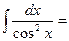 8о.
8о. 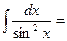 9о.
9о. 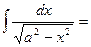 В частности,
В частности, 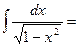 10о.
10о. 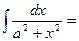 В частности,
В частности, 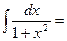
|
- Дать понятие интегральной суммы.
- Дать определение определенного интеграла.
- Перечислить основные свойства определенного интеграла (записать).
- Проанализируйте решение задач 8.1 - 8.3. Какие методы интегрирования здесь приведены?
8.1. 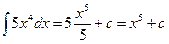 ;
;
8.2. 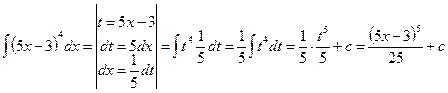 ;
;
8.3. 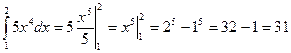 .
.
В следующих решениях необходимо найти, объяснить ошибки и исправить их (если они есть):
8.4. 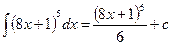 ;
;
8.5. 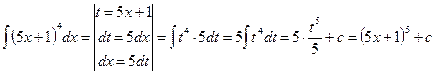 ;
;
8.6. 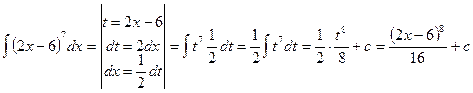 ;
;
8.7. 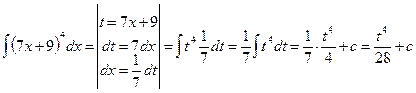 ;
;
8.8. 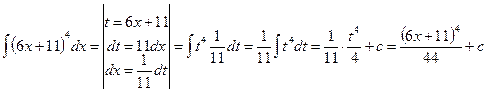 ;
;
8.9. 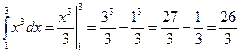 ;
;
8.10. 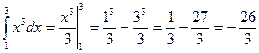 ;
;
8.11. 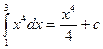 ;
;
8.12. 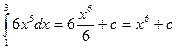 .
.
- Найти неопределенный интеграл:
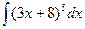 .
. - Найти неопределенный интеграл:
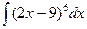 .
. - Найти неопределенный интеграл:
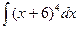 .
. - Пользуясь решением задач 8.1 - 8.3, вычислите следующий интеграл или определите, каких знаний не хватает для этого; в последнем случае попробуйте предложить свой алгоритм или вариант решения:
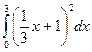 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 10
ОЦЕНОЧНОЕ СРЕДСТВО № 11
Пакет преподавателя
Справочный материал
Формула для расчета перемещения неравномерного движения: 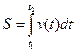 .
.
Зависимость между работой и силой выражается с помощью определенного интеграла: 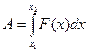 .
.
Вариант 1
7. R = 60 / 0,02 = 3000 и, следовательно,
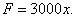
Растянуть пружину надо на 0,06 (м). Отсюда
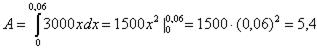
8.

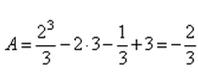
Вариант 2
6. По закону Гука сила F, растягивающая пружину, пропорциональна растяжению пружины, т.е. F = Rx. Из условия задачи R = 10 / 0,02, следовательно,
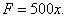
Значит,
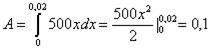
7. F = Rx, где х – величина деформации. При х = 0,01 м имеем R:
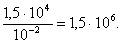
Отсюда:
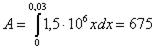
8.

Ответ: 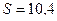 км.
км.
ОЦЕНОЧНОЕ СРЕДСТВО № 12
РЕФЕРАТИВНОЕ ЗАДАНИЕ
Раздел 2. Комплексные числа
Форма выполнения задания: внеаудиторная самостоятельная работа студентов.
В период написания рефератов преподаватель проводит индивидуальные консультации для студентов
Время на выполнение: 6 часов
Инструкция для студентов
Уважаемые студенты! Реферат выполняется в соответствии с методическими рекомендациями по его выполнению, оформляется в бумажном варианте в соответствии со стандартом колледжа и сдается преподавателю в указанные им сроки.
В процессе работы над рефератом вам необходимо спланировать информационный поиск. Рекомендуем воспользоваться Федеральным государственным образовательным стандартом по своей специальности (в котором вы можете найти требования к специалисту и содержание учебной дисциплины Математика), изучить статьи по соответствующим разделам математики, техническую литературу и современные научные разработки в области машиностроения, актуальную нормативно-правовую документацию по специальности, а также самостоятельно подобрать литературу и другие источники, в том числе Интернет-ресурсы.
В основную часть реферата необходимо включить главу, содержащую информацию о применении понятийного и методологического аппарата теории комплексных чисел при разработке и внедрении управляющих программ обработки деталей. Например, если обрабатываемый контур представляет собой ломаную линию, то с помощью прямоугольной системы координат можно легко задать все характерные точки его профиля; однако ситуация меняется, если необходимо выполнить на плоскости сверление группы отверстий, расположенных по окружности. Если для одного отверстия координаты расположения его оси в прямоугольной системе координат можно рассчитать достаточно просто, то расчет расположения осей для всех других отверстий будет гораздо более трудоемким. В этом случае вычисления удобнее выполнять в полярной системе координат, где положение точки на плоскости определяется расстоянием (радиусом) r от точки до начала координат и углом между определенной осью координат и радиусом, проведенным в точку из начала координат.
Также в реферат включаются решения задач (из сборников или составленных самостоятельно) на выполнение действий над комплексными числами.
Защита реферата проводится в устной форме в рамках теоретических занятий. По желанию студента защита может сопровождаться электронной презентацией. При оценке реферата принимаются во внимание его исследовательский характер, грамотность изложенного материала, полнота раскрытия темы, наличие обоснованных выводов и его оформление.
Темы рефератов
- История комплексных чисел.
- Комплексные числа и действия над ними.
- Тригонометрическая форма комплексного числа.
- Показательная форма комплексного числа.
- Применение комплексных чисел.
- Полярная система координат и ее применение.
ОЦЕНОЧНОЕ СРЕДСТВО № 13
Справочный материал
В машиностроении широко применяется математическое моделирование. Математическая модель – приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Например, можно построить математическую модель сверления лазером, математическую модель работы газотурбинного двигателя, математическую модель силы резания токарной операции. Часто в качестве аппарата для построения математических моделей используются понятия линейной алгебры – системы линейных уравнений, матрицы и определители. Множество объектов рассматривают как преобразователи, для которых каждому входу соответствует некоторый выход. Так, если изучают задачу о прогибе прямолинейного стержня под действием поперечной распределенной нагрузки, то входом можно считать ее плотность, а выходом – прогиб. Решение уравнений математической модели будет являться выходом.
В процедурах, относящихся к конструкторскому аспекту проектирования, преобладает использование математических моделей, отражающих структурные свойства объекта, например его геометрическую форму, размеры, взаимное расположение элементов в пространстве, т. е. структурные модели, которые часто представляются в виде матриц.
Вариант 1
1. 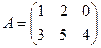 ,
, 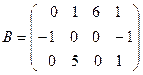 . Найти
. Найти 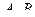 .
.
2. 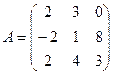 ,
, 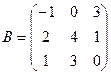 . Найти C=A+B, C=2B, C=3A, C=2A-B.
. Найти C=A+B, C=2B, C=3A, C=2A-B.
Вариант 2
1. 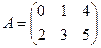 ,
, 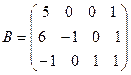 . Найти
. Найти 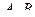 .
.
2. 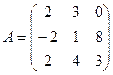 ,
, 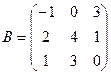 . Найти C=2A, C=A-B, C=A+3B, C=A-4B.
. Найти C=2A, C=A-B, C=A+3B, C=A-4B.
Вариант 3
1. 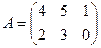 ,
, 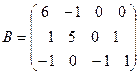 . Найти
. Найти 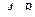 .
.
2. 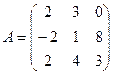 ,
, 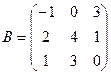 . Найти C=4B, C=4A-B, C=3A+B, C=A+2B.
. Найти C=4B, C=4A-B, C=3A+B, C=A+2B.
Пакет преподавателя
Вариант 1
2. 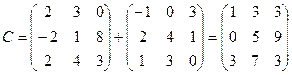 ;
;
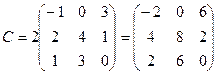 ;
; 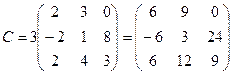 ;
;
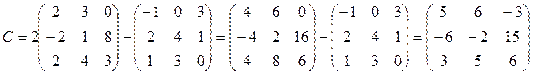 .
.
Вариант 2
2. 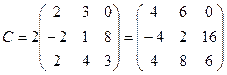 ;
;
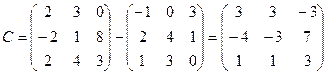 ;
;
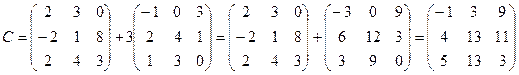 ;
;
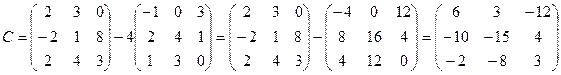 .
.
Вариант 3
2. 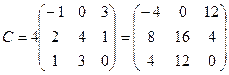 ;
;
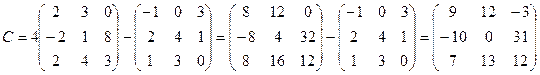 ;
;
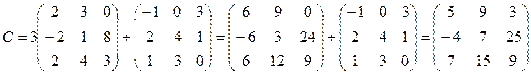 ;
;
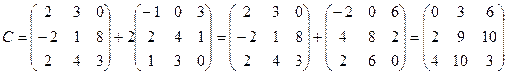 .
.
ОЦЕНОЧНОЕ СРЕДСТВО № 14
Справочный материал
В машиностроении широко применяется математическое моделирование. Математическая модель – приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Например, можно построить математическую модель сверления лазером, математическую модель работы газотурбинного двигателя, математическую модель силы резания токарной операции. Часто в качестве аппарата для построения математических моделей используются понятия линейной алгебры – системы линейных уравнений, матрицы и определители. Множество объектов рассматривают как преобразователи, для которых каждому входу соответствует некоторый выход. Так, если изучают задачу о прогибе прямолинейного стержня под действием поперечной распределенной нагрузки, то входом можно считать ее плотность, а выходом – прогиб. Решение уравнений математической модели будет являться выходом.
В процедурах, относящихся к конструкторскому аспекту проектирования, преобладает использование математических моделей, отражающих структурные свойства объекта, например его геометрическую форму, размеры, взаимное расположение элементов в пространстве, т. е. структурные модели, которые часто представляются в виде матриц.
Вариант 1
1. Вычислить определители:
а) 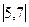 ; б)
; б) 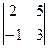 ; в)
; в) 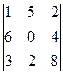 .
.
2. Вычислить определители четвертого порядка:
а) 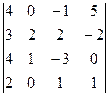 ; б)
; б) 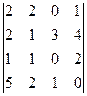 ; в)
; в) 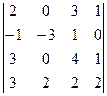 .
.
Вариант 2
1. Вычислить определители:
а) 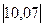 ; б)
; б) 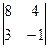 ; в)
; в) 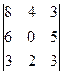 .
.
2. Вычислить определители четвертого порядка:
а) 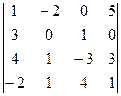 ; б)
; б) 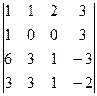 ; в)
; в) 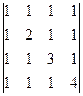 .
.
Вариант 3
1. Вычислить определители:
а) 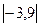 ; б)
; б) 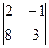 ; в)
; в) 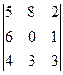 .
.
2. Вычислить определители четвертого порядка:
а) 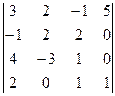 ; б)
; б) 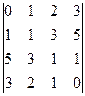 ; в)
; в) 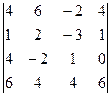 .
.
Пакет преподавателя
Вариант 1
2. б) –24; в) 5.
Вариант 2
2. б) 50; в) 6.
Вариант 3
2. б) –18; в) –144.
ОЦЕНОЧНОЕ СРЕДСТВО № 15
Справочный материал
В машиностроении широко применяется математическое моделирование. Математическая модель – приближённое описание какого-либо класса явлений внешнего мира, выраженное с помощью математической символики. Например, можно построить математическую модель сверления лазером, математическую модель работы газотурбинного двигателя, математическую модель силы резания токарной операции. Часто в качестве аппарата для построения математических моделей используются понятия линейной алгебры – системы линейных уравнений, матрицы и определители. Множество объектов рассматривают как преобразователи, для которых каждому входу соответствует некоторый выход. Так, если изучают задачу о прогибе прямолинейного стержня под действием поперечной распределенной нагрузки, то входом можно считать ее плотность, а выходом – прогиб. Решение уравнений математической модели будет являться выходом.
В процедурах, относящихся к конструкторскому аспекту проектирования, преобладает использование математических моделей, отражающих структурные свойства объекта, например его геометрическую форму, размеры, взаимное расположение элементов в пространстве, т. е. структурные модели, которые часто представляются в виде матриц.
Вариант 1
1. Решить систему линейных уравнений методом обратной матрицы.
2. Решить систему линейных уравнений по формулам Крамера.
3. Решить систему линейных уравнений методом Гаусса.
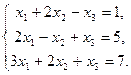
Вариант 2
1. Решить систему линейных уравнений методом обратной матрицы.
2. Решить систему линейных уравнений по формулам Крамера.
3. Решить систему линейных уравнений методом Гаусса.
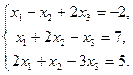
Вариант 3
1. Решить систему линейных уравнений методом обратной матрицы.
2. Решить систему линейных уравнений по формулам Крамера.
3. Решить систему линейных уравнений методом Гаусса.
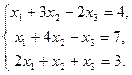
Вариант 4
1. Решить систему линейных уравнений методом обратной матрицы.
2. Решить систему линейных уравнений по формулам Крамера.
3. Решить систему линейных уравнений методом Гаусса.
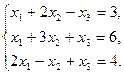
Вариант 5
1. Решить систему линейных уравнений методом обратной матрицы.
2. Решить систему линейных уравнений по формулам Крамера.
3. Решить систему линейных уравнений методом Гаусса.
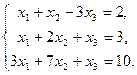
Вариант 6
1. Решить систему линейных уравнений методом обратной матрицы.
2. Решить систему линейных уравнений по формулам Крамера.
3. Решить систему линейных уравнений методом Гаусса.
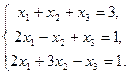
Пакет преподавателя
Вариант 1
1. 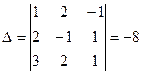 ;
; 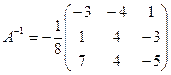 ;
;
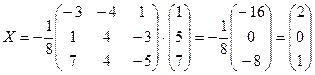 .
.
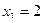 ,
, 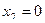 ,
, 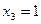 .
.
2. 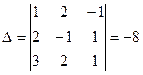 ,
, 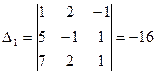 ,
,
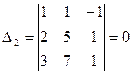 ,
, 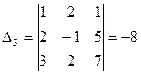 .
.
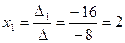 ,
, 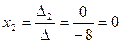 ,
, 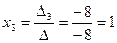 .
.
3. 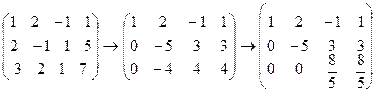 .
.
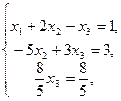
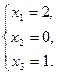
Вариант 2
5. 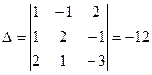 ;
; 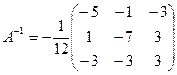 ;
;
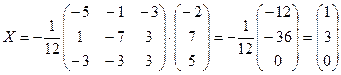 .
.
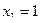 ,
, 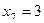 ,
, 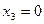 .
.
6. 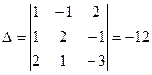 ,
, 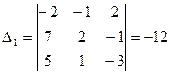 ,
,
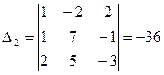 ,
, 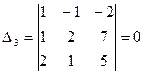 .
.
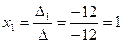 ,
, 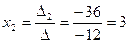 ,
, 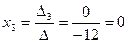 .
.
7. 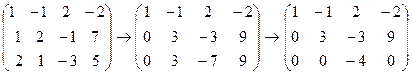 .
.
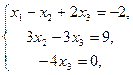
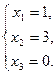
Вариант 3
5. 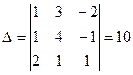 ;
; 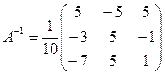 ;
;
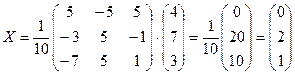 .
.
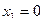 ,
, 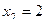 ,
, 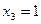 .
.
6. 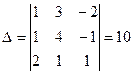 ,
, 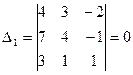 ,
,
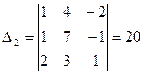 ,
, 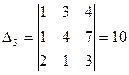 .
.
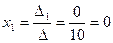 ,
, 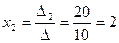 ,
, 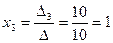 .
.
7. 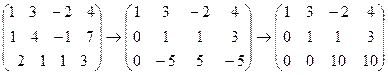 .
.
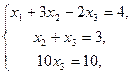
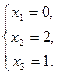
Вариант 4
5. 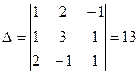 ;
; 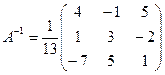 ;
;
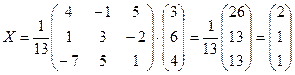 .
.
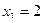 ,
, 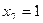 ,
, 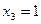 .
.
6. 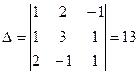 ,
, 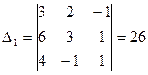 ,
,
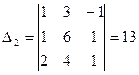 ,
, 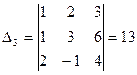 .
.
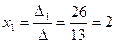 ,
, 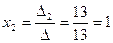 ,
, 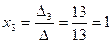 .
.
7. 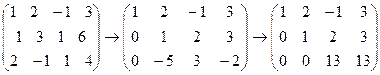 .
.
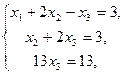
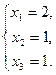
Вариант 5
1. 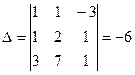 ;
; 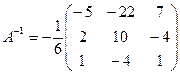 ;
;
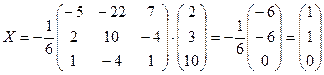 .
.
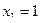 ,
, 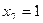 ,
, 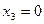 .
.
2. 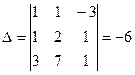 ,
, 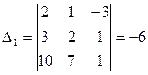 ,
,
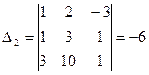 ,
, 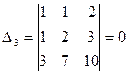 .
.
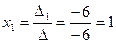 ,
, 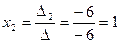 ,
, 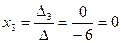 .
.
3. 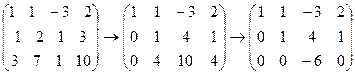 .
.
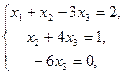
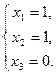
Вариант 6
4. 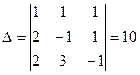 ;
; 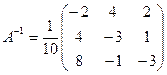 ;
;
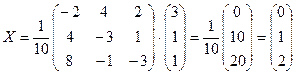 .
.
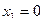 ,
, 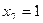 ,
, 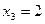 .
.
5. 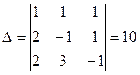 ,
, 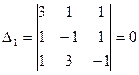 ,
,
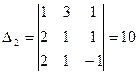 ,
, 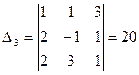 .
.
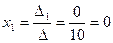 ,
, 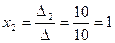 ,
, 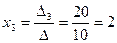 .
.
6. 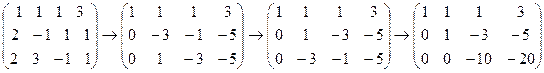 .
.
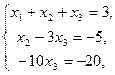
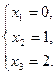
ОЦЕНОЧНОЕ СРЕДСТВО № 16
КЕЙС-задание
КЕЙС № 1
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, только во время операций на Курской дуге было израсходовано несколько миллионов патронов для пулеметов. Однако их нужно было не только изготовить, но и проверить качество. Проверка же порой занимает больше времени, чем изготовление. Методы проверки качества боеприпасов были предложены ещё в XIX веке простым математиком Михаилом Васильевичем Остроградским, но получили развитие и широкое применение лишь в XX веке, особенно в период Великой Отечественной войны и после её окончания. Активное участие в этой работе принял академик Андрей Николаевич Колмогоров и его ученики.
Тренировочная задача
Вероятность попадания в мишень при каждом выстреле для 1-го стрелка равна 0,7, а для 2-го – 0,8. Оба они делают по одному выстрелу по мишени, а затем каждый из стрелков стреляет еще раз, если при первом сделанном им выстреле он промахнулся. Найти вероятность того, что в мишени ровно 2 пробоины.
Задача для самостоятельного решения
Вероятность изготовления изделия с браком на оборонном предприятии равна 0,04. Перед выпуском изделие подвергается упрощенной проверке, которая в случае бездефектного изделия пропускает его с вероятностью 0,96, а в случае изделия с дефектом – с вероятностью 0,05. Определить: а) какая часть изготовленных изделий выходит с предприятия; б) какова вероятность того, что изделие, выдержавшее упрощенную проверку, бракованное?
КЕЙС № 2
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, видная роль в деле обороны нашей Родины принадлежит выдающемуся математику академику А.Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы нашими Военно-морскими силами. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или иных отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизнь многих людей, сберечь большие материальные ценности.
Тренировочная задача
В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.95, из обычной винтовки – 0.7. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
В сторону крейсера неприятеля подводной лодкой были выпущены 3 торпеды. Вероятность попадания первой торпеды равна 0,5, второй – равна 0,6, третьей – равна 0,8. При попадании одной торпеды вероятность того, что крейсер затонет, равна 0,3, при попадании двух торпед 0,6, а при попадании трёх торпед 1. Какова вероятность того, что неприятельский крейсер будет потоплен?
КЕЙС № 3
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, проблемы увеличения эффективности огня артиллерии и повышения меткости стрельбы в годы Великой Отечественной войны успешно решает академик А.Н. Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеяния артиллерийских снарядов. Математика помогла рассчитать, сколько нужно сделать одновременных выстрелов по самолёту противника для того, чтобы иметь наибольшую вероятность сбить его.
Тренировочная задача
В пирамиде 6 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.9, из обычной винтовки – 0.6. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
Батарея, состоящая из 3 орудий, ведет огонь по группе, состоящей из 5 самолетов. Каждое орудие выбирает себе цель случайно и независимо от других. Найти вероятность того, что все орудия будут стрелять: а) по одной и той же цели; б) по разным целям.
КЕЙС № 4
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, только во время операций на Курской дуге было израсходовано несколько миллионов патронов для пулеметов. Однако их нужно было не только изготовить, но и проверить качество. Проверка же порой занимает больше времени, чем изготовление. Методы проверки качества боеприпасов были предложены ещё в XIX веке простым математиком Михаилом Васильевичем Остроградским, но получили развитие и широкое применение лишь в XX веке, особенно в период Великой Отечественной войны и после её окончания. Активное участие в этой работе принял академик Андрей Николаевич Колмогоров и его ученики.
Тренировочная задача
Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания в мишень для первого стрелка равна 0,6, а для второго – 0,3. В мишени оказалась одна пробоина. Найти вероятность того, что она принадлежит первому стрелку.
Задача для самостоятельного решения
Брак в продукции военного завода вследствие дефекта А составляет 4%, а вследствие дефекта В – 3,5%. Годная продукция завода составляет 95%. Найти вероятность того что: а) среди продукции, не обладающей дефектом А, встретится дефект В; б) среди забракованной по признаку А продукции встретится дефект В.
КЕЙС № 5
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, видная роль в деле обороны нашей Родины принадлежит выдающемуся математику академику А.Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы нашими Военно-морскими силами. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или иных отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизнь многих людей, сберечь большие материальные ценности.
Тренировочная задача
В пирамиде 7 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.9, из обычной винтовки – 0.6. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
Батарея из трех орудий произвела залп, причем два снаряда попали в корабль. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны p 1 = 0,4, p 2 = 0,3, p 3 = 0,5.
КЕЙС № 6
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, проблемы увеличения эффективности огня артиллерии и повышения меткости стрельбы в годы Великой Отечественной войны успешно решает академик А.Н. Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеяния артиллерийских снарядов. Математика помогла рассчитать, сколько нужно сделать одновременных выстрелов по самолёту противника для того, чтобы иметь наибольшую вероятность сбить его.
Тренировочная задача
В пирамиде 6 винтовок, 4 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.95, из обычной винтовки – 0.8. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
Вероятность одного попадания в самолет неприятеля при одном залпе из двух орудий равна 0,38, а при выстреле из первого орудия вероятность попадания равна 0,8. Какова вероятность попадания при выстреле из второго орудия?
КЕЙС № 7
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, только во время операций на Курской дуге было израсходовано несколько миллионов патронов для пулеметов. Однако их нужно было не только изготовить, но и проверить качество. Проверка же порой занимает больше времени, чем изготовление. Методы проверки качества боеприпасов были предложены ещё в XIX веке простым математиком Михаилом Васильевичем Остроградским, но получили развитие и широкое применение лишь в XX веке, особенно в период Великой Отечественной войны и после её окончания. Активное участие в этой работе принял академик Андрей Николаевич Колмогоров и его ученики.
Тренировочная задача
Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры.
Задача для самостоятельного решения
При приеме партии боеприпасов подвергается проверке половина изделий. Условие приемки – наличие брака в выборке менее 2%. Вычислить вероятность того, что партия из 100 изделий, содержащая 5% брака, будет принята.
КЕЙС № 8
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, видная роль в деле обороны нашей Родины принадлежит выдающемуся математику академику А.Н. Крылову, чьи труды по теории непотопляемости и качки корабля были использованы нашими Военно-морскими силами. Он создал таблицы непотопляемости, в которых было рассчитано, как повлияет на корабль затопление тех или иных отсеков, какие номера отсеков нужно затопить, чтобы ликвидировать крен, и насколько это затопление может улучшить состояние корабля. Эти таблицы дали возможность спасти жизнь многих людей, сберечь большие материальные ценности.
Тренировочная задача
В пирамиде 7 винтовок, 4 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.95, из обычной винтовки – 0.7. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
Произведено три выстрела по кораблю неприятеля из орудия. Вероятность попадания при первом выстреле равна 0,75; при втором – 0,8; при третьем – 0,9. Определить вероятность того, что будет: а) три попадания; б) хотя бы одно попадание.
КЕЙС № 9
Справочный материал
Большой вклад в победу над фашистской Германией в Великой Отечественной войне 1941 – 1945 гг. внесли математики. Так, проблемы увеличения эффективности огня артиллерии и повышения меткости стрельбы в годы Великой Отечественной войны успешно решает академик А.Н. Колмогоров. По заданию Главного артиллерийского управления он, используя свои работы по математике в области теории вероятностей, дал определение наивыгоднейшего рассеяния артиллерийских снарядов. Математика помогла рассчитать, сколько нужно сделать одновременных выстрелов по самолёту противника для того, чтобы иметь наибольшую вероятность сбить его.
Тренировочная задача
В пирамиде 8 винтовок, 4 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле из винтовки с оптическим прицелом равна 0.95, из обычной винтовки – 0.8. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена.
Задача для самостоятельного решения
Вероятность одного попадания в самолет неприятеля при одном залпе из двух зенитных орудий равна 0,46. Найти вероятность попадания при одном выстреле второго орудия, если известно, что для первой эта вероятность равна 0,7.
Пакет преподавателя
КЕЙС № 1
Тренировочная задача
Пусть события: Ai, Bi – попадание в цель соответственно 1-м, 2-м стрелком при i-м выстреле (i=1,2);
С – в мишени ровно 2 пробоины.
Событие С произойдет, если:
- у каждого стрелка по одному попаданию с первого раза;
- у 1-го стрелка – попадание (при одном выстреле), у 2-го стрелка – промах и попадание;
- у 1-го стрелка – промах и попадание, у 2-го стрелка – попадание (при одном выстреле);
- у каждого стрелка – промах и попадание после двух выстрелов.
Итак,
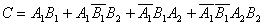
Используя теоремы сложения для несовместных и умножения для независимых событий, получим:
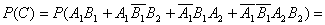
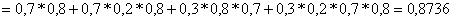
КЕЙС № 2
Задача для самостоятельного решения

КЕЙС № 5
Задача для самостоятельного решения

КЕЙС № 6
Задача для самостоятельного решения

КЕЙС № 9
Задача для самостоятельного решения
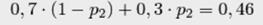
При работе над кейсом применяется групповая технология обучения, в рамках которой с помощью наблюдения за деятельностью студентов можно зафиксировать следующие поведенческие признаки:
- планирование студентами своей деятельности в рамках заданной технологии;
- обучение студентами других членов микрогрупп и всей группы рациональным приемам по организации деятельности для эффективного выполнения коллективного проекта;
- распределение студентами объема работы среди участников коллективного проекта;
- преодоление студентами кризисов взаимодействия совместно с членами группы.
Данные признаки нашли отражение в критериях оценки выполнения кейс-задания.
Кроме того, при наблюдении за выполнением студентами данного задания можно оценить, в какой мере каждый студент осознает и восполняет недостаток информации, освоенных умений и усвоенных знаний в процессе реализации деятельности, определяет стратегию решения проблемы, разбивает поставленную цель на задачи, проявляет патриотизм, анализирует полученные профессиональные знания применительно к военным технологиям.
ОЦЕНОЧНОЕ СРЕДСТВО № 17
исследовательское задание –
Справочный материал
Теория вероятностей и математическая статистика находит широкое применение в машиностроении, например, при проведении контроля соответствия качества деталей требованиям технической документации.
Форма выполнения задания: внеаудиторная самостоятельная работа студентов.
В период разработки электронных презентаций преподаватель проводит индивидуальные консультации для студентов
Время на выполнение: 12 часов
ОЦЕНОЧНОЕ СРЕДСТВО № 18
Вариант 1
- Производительности трех станков, обрабатывающих одинаковые детали, относятся как 1:3:6. Из нерассортированной партии обработанных деталей взяты наудачу две. Какова вероятность того, что: а) одна из них обработана на 3-м станке; б) обе обработаны на одном станке?
- У сборщика имеются 10 деталей, мало отличающихся друг от друга, из них четыре – первого, по две – второго, третьего и четвертого видов. Какова вероятность того, что среди шести взятых одновременно деталей три окажутся первого вида, два – второго и одна – третьего?
- Прибор, работающий в течение времени t, состоит из трех узлов, каждый из которых независимо от других может за это время выйти из строя. Неисправность хотя бы одного узла выводит прибор из строя целиком. Вероятность безотказной работы в течение времени t первого узла равна 0,9, второго – 0,95, третьего – 0,8. Найти вероятность того, что в течение времени t прибор выйдет из строя.
- Вся продукция цеха проверяется двумя контролерами, причем первый контролер проверяет 55% изделий, а второй – остальные. Вероятность того, что первый контролер пропустит нестандартное изделие, равна 0,01, второй – 0,02. Взятое наудачу изделие, маркированное как стандартное, оказалось нестандартным. Найти вероятность того, что это изделие проверялось вторым контролером.
- Контролер ОТК, проверив качество 20 изготовленных деталей, установил, что 16 из них стандартные, а остальные имеют дефекты. Найти вероятность того, что среди взятых наудачу из этой партии трех деталей: а) одна будет иметь дефект; б) две будут иметь дефект.
- Случайная величина Х задана законом распределения:
| 2 | 5 | 10 |
| 0,3 | 0,6 | 0,1 |
Найти:
а) математическое ожидание,
б) дисперсию,
в) среднее квадратичное отклонение этой случайной величины Х.
Вариант 2
- К распределительному устройству подключено три потребителя с номинальной мощностью 20, 15 и 5 кВт. Вероятность включенного состояния потребителей равна Р1 = 0,6, Р2 = 0,7; Р3 = 0,5. Определить вероятность того, что нагрузка на распределительном устройстве составит 40 кВт.
- Прибор состоит из двух узлов: работа каждого узла безусловно необходима для работы прибора в целом. Надежность (вероятность безотказной работы в течение времени t) первого узла равна 0,8, второго – 0,9. Прибор испытывался в течение времени t, в результате чего обнаружено, что он вышел из строя (отказал). Найти вероятность того, что отказал только первый узел, а второй исправен.
- Эксперт оценивает качественный уровень трех видов изделий по потребительским признакам. Вероятность того, что изделию первого вида будет присвоен знак качества, равна 0,7; для изделия второго вида эта вероятность равна 0,9; а для изделия третьего вида 0,8. Найти вероятность того, что знак качества будет присвоен: а) всем изделиям; б) только одному изделию; в) хотя бы одному изделию.
- При включении зажигания двигатель начнет работать с вероятностью 0,6. Найти вероятность того, что: а) двигатель начнет работать при третьем включении зажигания; б) для запуска двигателя придется включать зажигание не более трех раз.
- В коробке смешаны лампы одинакового размера и формы: по 100 Вт – 7 штук, по 75 Вт – 13 штук. Вынуты наудачу 3 лампы. Какова вероятность того, что: а) они одинаковой мощности; б) хотя бы две из них по 100 Вт?
- Случайная величина Х задана законом распределения:
| 3 | 8 | 11 |
| 0,2 | 0,5 | 0,3 |
Найти:
а) математическое ожидание,
б) дисперсию,
в) среднее квадратичное отклонение этой случайной величины Х.
Вариант 3
- Производятся испытания прибора. При каждом испытании прибор выходит из строя с вероятностью 0,8. После первого выхода из строя прибор ремонтируется; после второго признается негодным. Найти вероятность того, что прибор окончательно выйдет из строя в точности при четвертом испытании.
- Мастер обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания рабочего, равна 0,3, второй – 0,6, третий – 0,4 и четвертый – 0,25. Найти вероятность того, что в течение смены хотя бы один станок не потребует внимания мастера
- В среднем каждое сотое изделие, производимое предприятием, дефектное. Если взять два изделия, какова вероятность, что оба окажутся исправными?
- Завод выпускает определенного типа изделия; каждое изделие имеет дефект с вероятностью 0,7. После изготовления изделие осматривается последовательно тремя контролерами, каждый из которых обнаруживает дефект с вероятностями 0,8; 0,85; 0,9 соответственно. В случае обнаружения дефекта изделие бракуется. Определить вероятность того, что изделие: 1) будет забраковано; 2) будет забраковано: а) вторым контролером; б) всеми контролерами.
- Среди 20 станков 8 нуждаются в срочном техническом обслуживании. Какова вероятность того, что среди выбранных одновременно наудачу 3 станков по крайней мере два нуждаются в обслуживании?
- Случайная величина Х задана законом распределения:
| 4 | 3 | 7 |
| 0,1 | 0,4 | 0,5 |
Найти:
а) математическое ожидание,
б) дисперсию,
в) среднее квадратичное отклонение этой случайной величины Х.
Пакет преподавателя
Вариант 1
1. а) Обозначим события: Ai – деталь обработана на i-м станке (i = 1, 2, 3);
В – одна из двух взятых деталей обработана на 3-м станке.
По условию
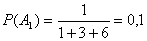
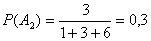
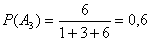
Очевидно, что B = A1A3+A2A3+A3A1+A3A2
(при этом надо учесть, что либо первая деталь обработана на 3-м станке, либо вторая).
По теоремам сложения и умножения (для независимых событий)
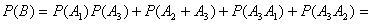
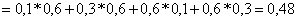
б) Пусть событие С – обе отобранные детали обработаны на одном станке.
Тогда C = A 1 A 1+A 2 A 2+A 3 A 3, P(C) = 0,1*0,1 + 0,3*0,3 + 0,6*0,6 = 0,46.
Вариант 2
4. а) Обозначим события: А – двигатель начнет работать при каждом включении зажигания;
В – то же при третьем включении зажигания.
Очевидно, что В = 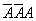 , Р(В) =
, Р(В) = 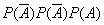 = 0,4*0,4*0,6 = 0,096.
= 0,4*0,4*0,6 = 0,096.
б) Пусть событие С – для запуска двигателя придется включать зажигание не более трех раз. Очевидно, событие С наступит, если двигатель начнет работать при 1-м включении, или при 2-м, или при 3-м включении, т.е. С = А+АА+ААА. Следовательно,
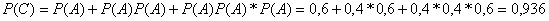
4. Программа промежуточной аттестации студентов
Промежуточная аттестация по дисциплине ЕН.01. Математика проводится в форме дифференцированного зачета.
При проведении промежуточной аттестации используются следующие оценочные средства:
- перечень теоретических вопросов к дифференцированному зачету,
- комплект практических заданий к дифференцированному зачету.
Перечень теоретических вопросов выдается студентам не позднее, чем за месяц до начала сессии.
Источники
ОИ - Основные источники учебной литературы:
1. Дадаян, А.А. Математика: учебник. – М.: ИНФРА-М, 2017.
2. Дадаян, А.А. Сборник задач по математике: учебное пособие. – М.: ФОРУМ: ИНФРА-М, 2013.
3. Омельченко, В.П. Математика: учеб. пособие / В.П. Омельченко, Э.В. Курбатова – Ростов н/Д: Феникс, 2013.
4. Богомолов Н.В. Практические занятия по математике. В 2 ч. Часть 1: учеб. пособие для СПО – М.: Издательство Юрайт, 2017.
5. Богомолов Н.В. Практические занятия по математике. В 2 ч. Часть 2: учеб. пособие для СПО – М.: Издательство Юрайт, 2017.
ДИ - Дополнительные источники:
1. Григорьев В.П. Математика: учебник для студ. учреждений сред. проф. образования / В.П. Григорьев, Т.Н. Сабурова. – М.: Издательский центр «Академия», 2017.
2. Богомолов, Н.В. Практические занятия по математике: учеб. пособие для бакалавров. – М.: Издательство Юрайт, 2013.
ОЦЕНОЧНОЕ СРЕДСТВО № 19
ОЦЕНОЧНОЕ СРЕДСТВО № 20
Ен .01. МАТЕМАТИКА
Специальность
27.02.07 Управление качеством продукции, процессов и услуг (по отраслям)
Квалификация выпускника
техник - технолог
Чебоксары, 2018
Фонд оценочных средств (далее – ФОС) по учебной дисциплине (далее – УД) ЕН.01. Математика программы подготовки специалистов среднего звена (ППССЗ) по специальности 27.02.07 Управление качеством продукции, процессов и услуг базового уровня разработан на основе Федерального государственного образовательного стандарта (далее – ФГОС) по специальности 27.02.07 Управление качеством продукции, процессов и услуг в соответствии с рабочей программой учебной дисциплины ЕН.01. Математика
Разработчик:
Леонтьева Т.Ю., преподаватель МЦК-ЧЭМК Минобразования Чувашии
СОГЛАСОВАНО
Председатель ЦК специальности (М) Л.Г. Андреева
Содержание
1. Область применения ФОС по учебной дисциплине ЕН.01. Математика
2. Программа текущего контроля успеваемости студентов
3. ФОС для проведения текущего контроля
4. Программа промежуточной аттестации студентов
5. ФОС для промежуточной аттестации
1. Область применения ФОС по учебной дисциплине ЕН.01. Математика
ФОС предназначен для проверки результатов освоения учебной дисциплины основной профессиональной образовательной программы (далее ОПОП) по специальности 15.02.15 Технология металлообрабатывающего производства.
ФОС позволяет оценивать следующие результаты освоения УД:
1. Элементы профессиональных компетенций (ПК) и общих компетенций (ОК):
Таблица 1
| Профессиональные и общие компетенции |
| ПК 1.3. Разрабатывать технологическую документацию по обработке заготовок на основе конструкторской документации в рамках своей компетенции в соответствии с нормативными требованиями, в том числе с использованием систем автоматизированного проектирования |
| ПК 1.4. Осуществлять выполнение расчётов параметров механической обработки и аддитивного производства в соответствии с принятым технологическим процессом согласно нормативным требованиям, в том числе с использованием систем автоматизированного проектирования |
| ПК 1.5. Осуществлять подбор конструктивного исполнения инструмента, материалов режущей части инструмента, технологических приспособлений и оборудования в соответствии с выбранным технологическим решением, в том числе с использованием систем автоматизированного проектирования |
| ПК 1.6. Оформлять маршрутные и операционные технологические карты для изготовления деталей на механических участках машиностроительных производств, в том числе с использованием систем автоматизированного проектирования |
| ПК 1.7. Осуществлять разработку и применение управляющих программ для металлорежущего или аддитивного оборудования в целях реализации принятой технологии изготовления деталей на механических участках машиностроительных производств, в том числе с использованием систем автоматизированного проектирования |
| ПК 1.10. Разрабатывать планировки участков механических цехов машиностроительных производств в соответствии с производственными задачами, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.3. Разрабатывать технологическую документацию по сборке узлов или изделий на основе конструкторской документации в рамках своей компетенции в соответствии с нормативными требованиями, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.4. Осуществлять выполнение расчётов параметров процесса сборки узлов или изделий в соответствии с принятым технологическим процессом согласно нормативным требованиям, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.5. Осуществлять подбор конструктивного исполнения сборочного инструмента, материалов исполнительных элементов инструмента, приспособлений и оборудования в соответствии с выбранным технологическим решением, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.6. Оформлять маршрутные и операционные технологические карты для сборки узлов или изделий на сборочных участках машиностроительных производств, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.7. Осуществлять разработку управляющих программ для автоматизированного сборочного оборудования в целях реализации принятой технологии сборки узлов или изделий на сборочных участках машиностроительных производств, в том числе с использованием систем автоматизированного проектирования |
| ПК 2.10. Разрабатывать планировки участков сборочных цехов машиностроительных производств в соответствии с производственными задачами, в том числе с использованием систем автоматизированного проектирования |
| ПК 3.1. Осуществлять диагностику неисправностей и отказов систем металлорежущего и аддитивного производственного оборудования в рамках своей компетенции для выбора методов и способов их устранения |
| ПК 3.4. Организовывать ресурсное обеспечение работ по наладке металлорежущего и аддитивного оборудования в соответствии с производственными задачами, в том числе с использованием SCADA систем |
| ПК 3.5. Контролировать качество работ по наладке, подналадке и техническому обслуживанию металлорежущего и аддитивного оборудования и соблюдение норм охраны труда и бережливого производства, в том числе с использованием SCADA систем |
| ПК 4.1. Осуществлять диагностику неисправностей и отказов систем сборочного производственного оборудования в рамках своей компетенции для выбора методов и способов их устранения |
| ПК 4.4. Организовывать ресурсное обеспечение работ по наладке сборочного оборудования в соответствии с производственными задачами, в том числе с использованием SCADA систем |
| ПК 4.5. Контролировать качество работ по наладке, подналадке и техническому обслуживанию сборочного оборудования и соблюдение норм охраны труда и бережливого производства, в том числе с использованием SCADA систем |
| ПК 5.2. Организовывать определение потребностей в материальных ресурсах, формирование и оформление их заказа с целью материально-технического обеспечения деятельности структурного подразделения |
| ОК 01. Выбирать способы решения задач профессиональной деятельности, применительно к различным контекстам |
| ОК 02. Осуществлять поиск, анализ и интерпретацию информации, необходимой для выполнения задач профессиональной деятельности |
| ОК 09. Использовать информационные технологии в профессиональной деятельности |
| ОК 10. Пользоваться профессиональной документацией на государственном и иностранном языках |
2. Знания и умения:
Таблица 2
| Знания: |
| основные математические методы решения прикладных задач |
| основы дифференциального и интегрального исчислений |
| основные методы и понятия математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики |
| роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности |
| Умения: |
| анализировать сложные функции и строить их графики |
| выполнять действия над комплексными числами |
| вычислять значения геометрических величин |
| производить действия над матрицами и определителями |
| решать задачи на вычисление вероятности с использованием элементов комбинаторики |
| решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений |
| решать системы линейных уравнений различными методами |
Перечень рекомендуемых учебных изданий,
дополнительной литературы, Интернет-ресурсов
ОИ - Основные источники учебной литературы:
1. Дадаян, А.А. Математика: учебник. – М.: ИНФРА-М, 2017.
2. Дадаян, А.А. Сборник задач по математике: учебное пособие. – М.: ФОРУМ: ИНФРА-М, 2013.
3. Омельченко, В.П. Математика: учеб. пособие / В.П. Омельченко, Э.В. Курбатова – Ростов н/Д: Феникс, 2013.
4. Богомолов Н.В. Практические занятия по математике. В 2 ч. Часть 1: учеб. пособие для СПО – М.: Издательство Юрайт, 2017.
5. Богомолов Н.В. Практические занятия по математике. В 2 ч. Часть 2: учеб. пособие для СПО – М.: Издательство Юрайт, 2017.
ДИ - Дополнительные источники:
1. Григорьев В.П. Математика: учебник для студ. учреждений сред. проф. образования / В.П. Григорьев, Т.Н. Сабурова. – М.: Издательский центр «Академия», 2017.
2. Богомолов, Н.В. Практические занятия по математике: учеб. пособие для бакалавров. – М.: Издательство Юрайт, 2013.
2. Программа текущего контроля успеваемости студентов
Текущий контроль освоения студентами материала учебной дисциплины ЕН.01. Математика состоит из следующих видов: оперативный и рубежный контроль.
При проведении текущего контроля используются следующие методы:
- аудиторная контрольная работа;
- проверочная работа;
- письменное тестирование;
- комбинированный (уплотненный) опрос;
- кейс-задание;
- реферативное задание – выполнение и защита реферата;
- исследовательское задание – создание и защита электронной презентации;
- индивидуальное творческое задание – сочинение.
При проведении аудиторной контрольной работы студент прочитывает задания соответствующего варианта контрольной работы и отвечает письменно на вопросы (решает задания) в любом порядке. Время выполнения контрольной работы: 45 мин.
Проверочная работа в отличие от контрольной работы характеризуется меньшим охватом проверяемых тем (разделов) и меньшим временем, отведенным на ее выполнение в рамках аудиторного занятия (20-25 мин.).
При проведении письменного тестирования студенты должны внимательно прочитать задания теста и выбрать правильные ответы из предложенных вариантов. Количество правильных ответов и максимальное время прохождения теста указывается в задании в зависимости от темы и количества вопросов в тесте.
Комбинированный (уплотненный) опрос проводится следующим образом: вызываются одновременно 4-5 студентов. Один отвечает устно как при индивидуальном опросе. Остальные письменно: двое у доски выполняют задание, двое за партой на листочках. Выслушав устный ответ, преподаватель проверяет письменные ответы у доски (за партой). После этого задает по 1-2 небольших вопроса и ставит всем оценки. Фронтально можно спросить еще нескольких студентов, например, проверить выполнение студентами домашнего задания, повторить пройденное, выяснить готовность группы к изучению нового материала, определить сформированность основных понятий, усвоение нового учебного материала, который был только что разобран на занятии. Положительные моменты комбинированного опроса: 1) позволяет в течение 20 минут спросить 8-10 человек, 2) дает возможность выработать умение решать задачи, 3) позволяет за небольшой отрезок времени проверить знания студентов по большому разделу программы.
В основе выполнения заданий по анализу конкретных ситуаций (кейсов, кейс-заданий) лежит имитационное моделирование, другими словами, применению этого метода в обучении предшествует разработка конкретного примера или использование готовых материалов с описанием ситуации реальной профессиональной деятельности. Кейс-технологии за счет ориентации на конкретные, практические проблемы, которые призваны решать специалисты очень многих сфер деятельности, позволяют повышать мотивацию учения у студентов, так как им становится понятным, зачем, в какой ситуации может пригодиться тот или иной учебный материал, как применить его в конкретной практической деятельности. Студенты получают кейс и работают с ним непосредственно на занятии (задания могут быть разными для микрогрупп или дается одно задание для всех). После совместного с преподавателем определения места кейса в учебном курсе и вовлечения студентов в анализ реальной ситуации организуется обсуждение ситуации в микрогруппах и подготовка решения. Результатом работы с кейсом является представление и обоснование членами микрогрупп решения по кейсу.
Реферат выполняется в соответствии с методическими рекомендациями по его выполнению, оформляется в бумажном варианте в соответствии со стандартом колледжа и по желанию студента может сопровождаться электронной презентацией. Защита реферата проводится в устной форме в рамках теоретических занятий.
Электронная презентация разрабатывается группой студентов (2-3 чел.) в соответствии с методическими рекомендациями по ее подготовке. Защита презентации проводится в устной форме в рамках теоретических занятий. При подготовке выступления по презентации можно руководствоваться рекомендациями к подготовке устного сообщения.
Математическое сочинение – одна из возможных форм творческой работы студентов при обучении математике. Здесь речь идет о написании, составлении именно математического сочинения, а не о литературной обработке изученного математического материала. В процессе работы над сочинением студенты могут самостоятельно подбирать литературу. В период написания домашних сочинений преподаватель проводит индивидуальные консультации для студентов. При написании математических сочинений студенты выполняют разные виды деятельности: самостоятельное изучение литературы; отбор материала по выбранной теме; связное изложение материала; проведение небольших самостоятельных исследований; подбор или (и) самостоятельное составление задач и их решение. Наиболее интересны и ценны сочинения, при составлении которых студент выполнил некоторые исследования. Сочинения выполняются на двойном тетрадном листе рукописным способом или печатаются на отдельных листах формата А4.
Дата: 2019-03-05, просмотров: 718.