Формула (71) выражает теорему Кориолиса: абсолютное ускорение точки равно сумме переносного, относительного ускорений и кориолисова, равного

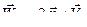 .                                                        (72)

Модуль ускорения Кориолиса 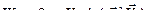, а направление определяется по правилу векторного произведения.

Ускорение Кориолиса равно нулю, если:

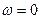-  (переносное движение поступательное либо равенство справедливо в некоторые моменты времени) ,

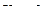- ( равенство справедливо в некоторые моменты времени),

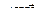-   (векторы, входящие в (72) параллельны).

Заметим, что в формулах (59) для вычисления ускорения точки при плоскопараллельном движении тела имеет место первый из оговоренных случаев.

После формулы (68) наличие последнего слагаемого в формуле (71) может вызвать недоумение. Ниже на простом примере показано, что в общем случае  .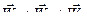

Рассмотрим круглую платформу радиуса R, вращающуюся вокруг своего центра О с постоянной угловой скоростью 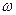 (рис.81). По краю платформы пустим точку М так, чтобы она все время находилась напротив маяка А, установленного на неподвижном основании. Очевидно, что в неподвижной системе отсчета точка М покоится, т.е. ее абсолютные скорость и ускорение равны нулю.

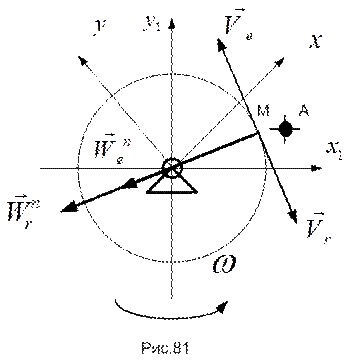
Принимая движение точки М по платформе за относительное, а движение совпадающей с ней точки – за переносное, имеем

 ;  ; .

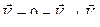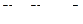Ускорения точки М в указанных движениях будут равны своим нормальным составляющим. Последние направлены от точки М к центру платформы и равны 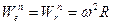 . Их сумма не равна нулю, что противоречит здравому смыслу (неподвижность точки М).

Появление ускорения Кориолиса объясняется взаимовлиянием переносного и относительного движений, которое отсутствует при независимом рассмотрении картин составляющих движений.

Задачи на сложное движение точки подразделяются на два типа: в первом по известным переносному и относительному движениям определяют абсолютное, во втором известное абсолютное движение раскладывают на интересующие составляющие.  

ПРИМЕР  29  (продолжение решения ПРИМЕРА 27). Шайба М движется по горизонтальному стержню ОА так, что 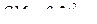. В то же время стержень вращается вокруг вертикальной оси, проходящей через точку О, по закону 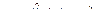. Определить радиальную и трансверсальную составляющие абсолютного ускорения шайбы в момент времени .

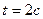РЕШЕНИЕ. Примем за относительное движение шайбы ее движение вдоль стержня ОА по закону 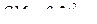; картина этого движения (КОД) и его кинематические характеристики, вычисленные для момента времени 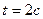, изображены на рис.82.а.  

;

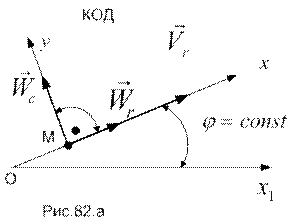
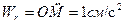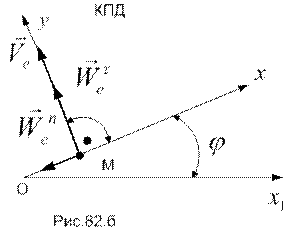
Переносным движением шайбы М будет движение точки стержня, находящейся в рассматриваемый момент времени под шайбой. Тогда ; .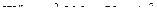

Картина переносного движения (КПД) и вычисленные для него кинематические характеристики изображены на рис.82.б.

Ускорение Кориолиса равно 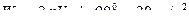, его направление см. на рис.82.а. 

Теперь вычислим радиальную (проекции на ось Оx подвижной координатной системы) составляющую абсолютного ускорения:

.

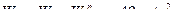Трансверсальная (проекции на ось Oy подвижной координатной системы) составляющая абсолютного ускорения будет

.

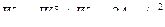При необходимости можно найти величину абсолютного ускорения шайбы как геометрическую сумму ее составляющих.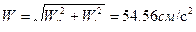

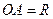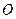ПРИМЕР 30. Кривошип  кривошипно-кулисного механизма вращается с постоянной угловой скоростью  вокруг оси . На расстоянии  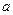по вертикали вниз расположена ось вращения  кулисы, длина которой 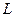. Найти скорость и ускорение точки В кулисы, когда кривошип занимает горизонтальное положение (рис 83.а). 

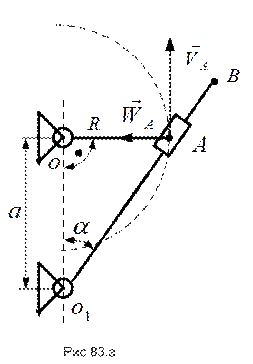
РЕШЕНИЕ. Задание движения кривошипа позволяет рассчитать скорость и ускорение центра ползуна А, как

.

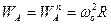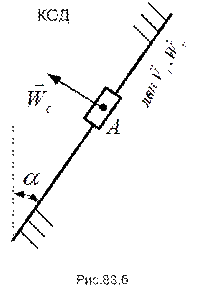
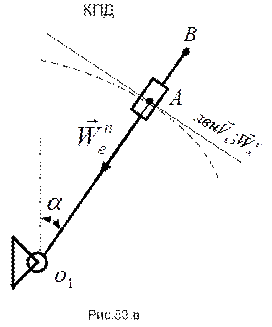
Движение точки А по окружности представим как сложное движение, состоящее из относительного движения вдоль кулисы 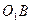 и переносного движения вместе с точкой кулисы 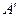, совпадающей в данный момент времени с точкой А.

Такой подход позволяет рассмотреть независимо картины относительного (рис.83.б) и переносного (рис.83.в) движений точки А, находя интересующие нас глобальные кинематические характеристики переносного движения.

Построим треугольник скоростей (см. рис.84.а) :

.

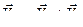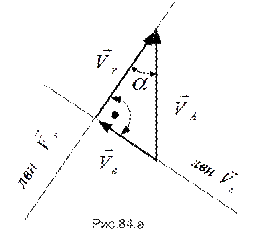
Из треугольника находим, что

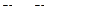
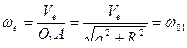 Построим многоугольник ускорений (см. рис.84.б):

;

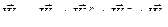при этом учтено, что

.

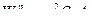
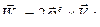
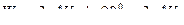Направление ускорения Кориолиса указано на картине относительного движения (рис.83.б).

.  

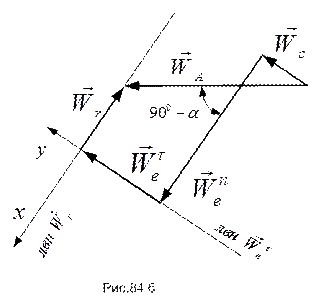
Проецируя многоугольник на оси выбранной координатной системы, получим два уравнения для вычисления неизвестных составляющих 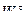 и :

.

Вычислив тангенциальную составляющую переносного ускорения

,

найдем угловое ускорение кулисы  .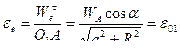

Теперь вычислить кинематические характеристики точки В не представляет затруднений:

.

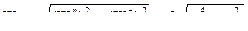Вопросы и задачи для самоконтроля

1. Дайте определения абсолютного, относительного и переносного движений точки.

2. Что происходит с параметрами переносного движения при рассмотрении картины относительного движения (и наоборот)?

3. В каком случае производные, вычисленные в неподвижной и подвижной координатных системах, оказываются равными?

4. Запишите формулы, связывающие скорости и ускорения в подвижной и неподвижной системах отсчета.

5. Запишите формулу для вычисления ускорения Кориолиса. В каких случаях оно обращается в нуль?

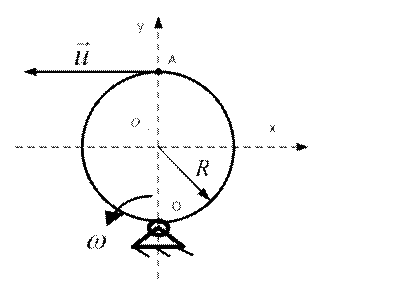
6. Диск равномерно вращается вокруг оси, перпендикулярной его плоскости и проходящей через точку О обода. По ободу с постоянной по величине скоростью 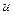движется точка А. Найти ускорение точки А в указанном положении.  

Лекция 9