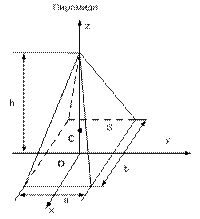
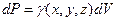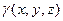Выделим в неоднородном твердом теле элементарный объем dV=dx dy dz (рис.31). Вес выделенного элемента будет , где – удельный вес в точке тела с соответствующими координатами.

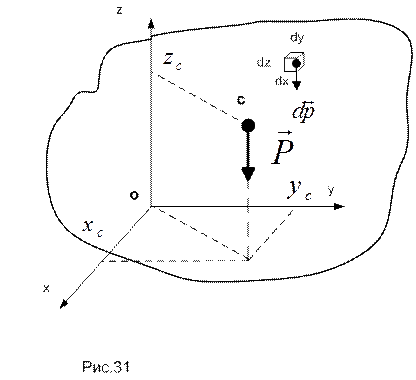
Веса элементов образуют систему сил, параллельных оси аппликат. Модуль равнодействующей

 весов элементов называется весом твердого тела, а геометрическая точка приложения равнодействующей – центром тяжести твердого тела. Для вычисления этих величин воспользуемся формулами (11) и (13), заменив в них суммирование интегрированием по объему, то есть

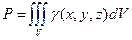                                            (16)

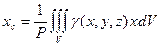                                    (17)

Величина, стоящая в числителе формулы (17), называется статическим моментом веса твердого тела относительно координатной плоскости .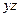  

 Структура формул для вычисления 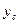 и  аналогичная.

Очевидно, что для однородного тела формула (17) принимает вид

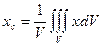                                                    (18)

Структура формул для вычисления 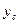 и 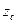 аналогичная.

В этом случае центр тяжести твердого тела совпадает центром его объема.

Если один из размеров твердого тела существенно меньше двух других, тело называют тяжелой поверхностью. При неизменном весе единицы площади поверхности она является однородной. Формулы для вычисления  веса и координат центра тяжести получаются из (16) – (18) заменой интегралов по объему на интегралы по поверхности. В некоторых случаях поверхность может быть плоской.

Если два размера твердого тела существенно меньше третьего, тело называют тяжелой линией. При неизменном весе единицы длины линии она является однородной. Формулы для вычисления веса и координат центра тяжести получаются из (16) – (18) заменой интегралов по объему на криволинейные интегралы. В некоторых случаях линия может быть прямой.

Если однородное твердое тело имеет плоскость симметрии, то центр тяжести тела лежит в этой плоскости (сумма статических моментов элементарных сил веса относительно плоскости симметрии равна нулю).

Если однородное твердое тело имеет две плоскости симметрии, то центр тяжести тела принадлежит линии пересечения этих плоскостей.

Если однородное твердое тело имеет три плоскости симметрии, то центр тяжести тела расположен в точке их пересечения.

Если твердое тело может быть мысленно расчленено на элементы, веса и положения центров тяжести которых известны, то вычисление веса твердого тела и положения его центра тяжести может быть выполнено по формулам (11) и (13). Так, например, рассчитываются вес и координаты центра тяжести строящегося судна.

Если тело имеет вырезы, то они могут быть учтены как элементы отрицательного веса. 

Заметим, что  в инженерной справочной литературе приводится достаточно большое количество однородных элементов (объемных, плоских и криволинейных), для которых рассчитаны веса и положения центров тяжести. Ниже в таблице приведены некоторые из  них. 

Вид элемента	Объем (площадь) элемента	Абсцисса ц.т.	Ордината ц.т.	Аппликата ц.т.
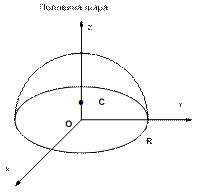
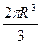
		0	0
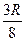
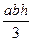
		0	0
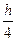
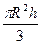
		0	0
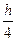
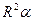
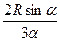
			0	0
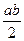
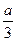
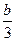
				0

В некоторых ситуациях положение центра тяжести твердого тела может быть найдено по результатам эксперимента. Например, при подвешивании тела на нити, его центр тяжести располагается на линии нити. Подвесив тело за другую точку, не лежащую на первой линии, найдем положение центра тяжести тела как точку пересечения двух линий. Другим способом, применяемым для нахождения центра тяжести протяженных тел, является так называемая постановка его на «ножи» с параллельными лезвиями. При сближении «ножей» центр тяжести тела стремится остаться между ними и, в пределе, оказывается на линии совпадения лезвий.

В инженерной практике для определения положения центра тяжести тела могут применяться способы, являющиеся комбинацией расчета и  эксперимента. В качестве примера приведем вычисление удаления центра тяжести самолета, изображенного на рис.32, от его переднего колеса.

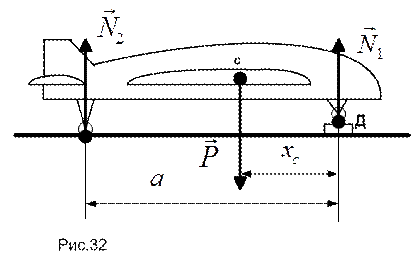
На рисунке: Д- динамометр, показывающий величину силы 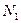 нормального давления переднего колеса, P – вес самолета,  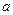– расстояние от переднего колеса до оси задних колес.

Очевидно, что интересующее расстояние от переднего колеса до линии силы веса самолета может быть получено из уравнения суммы моментов сил 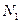  и P относительно оси задних колес, как

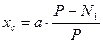
Замечание: если вес Р самолета не известен, то, переставив динамометр Д под задние колеса, можно получить величину силы нормального давления 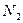. Тогда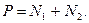

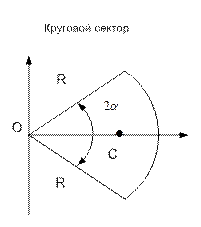
ПРИМЕР 7. Для однородной пластины, имеющей форму кругового сектора с углом 2 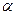при вершине (см. рис. 33), найти положение центра тяжести пластины. 

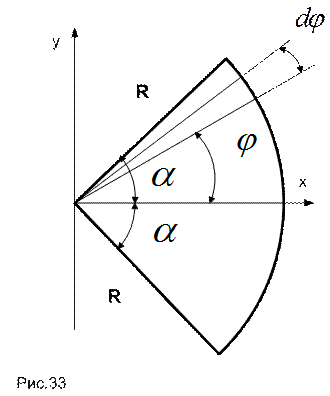
Проведем ось абсцисс так, что бы она являлась биссектрисой угла 2 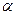. Тогда, в силу симметрии, ордината центра тяжести равна нулю, т.е. .

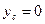Двумя радиусами, элементарный угол между которыми 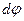, выделим на пластине элемент, площадь которого приближенно равна площади равнобедренного треугольника  

.

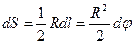Абсцисса центра тяжести выделенного треугольного элемента равна .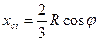

Теперь можно составить выражение для вычисления абсциссы центра тяжести кругового сектора как

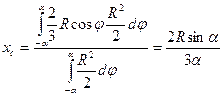
Замечание: при вычислении учтено, что центр тяжести однородного плоского тела имеет на плоскости те же координаты, что и у соответствующей плоской фигуры.

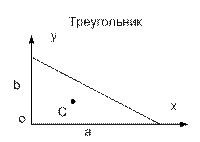
ПРИМЕР 8. Для тонкой однородной пластины сложной формы, размеры которой указаны на рис.34, найти положение центра тяжести.

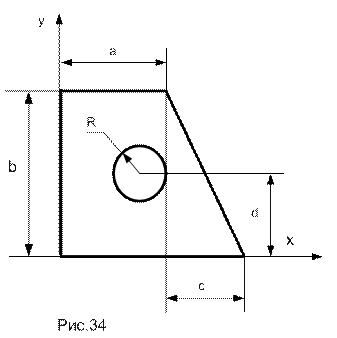
Мысленно расчленим пластину на три элемента: прямоугольник, треугольник и круг. Для каждого из элементов найдем площадь и координаты центра тяжести:

;

;

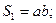
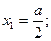
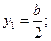
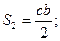
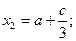
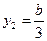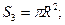
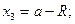
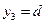Тогда для пластины координаты центра тяжести можно вычислить по формулам:

.

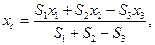
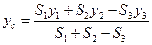При вычислении отверстие трактовалось как присоединение круга отрицательного веса.

Вопросы и задачи для самоконтроля

1.  Верна ли приведенная ниже формула для нахождения абсциссы центра параллельных сил?

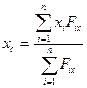
2.  Получите самостоятельно формулы для равнодействующей и абсциссы центра приложения нагрузки, равномерно распределенной вдоль оси абсцисс.

3.  Прямоугольный понтон имеет длину  L , ширину  B и осадку T. Определите величины равнодействующих сил давления воды на борта и днище понтона, а так же координаты точек приложения этих сил.

4.  Как изменились бы формулы, полученные при решении примера 8, если бы тонкая пластина состояла из элементов с разными удельными весами (например, удельный вес прямоугольника 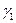, а треугольника - )?

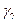5.  Определите координаты центра тяжести тонкой однородной пластины прямоугольной (треугольной) формы.

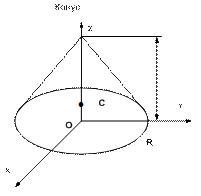
6.  Определите аппликату центра тяжести однородного прямоугольного параллелепипеда (пирамиды, кругового конуса).

Лекция 4