Дискретная случайная величина.
Дискретной называют случайную величину, возможные значения которой есть отдельные изолированные числа (т.е. между двумя соседними возможными значениями нет других возможных значений), которые эта величина принимает с определенными вероятностями.
Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих и вероятностей, заданный в виде таблицы:
X x1 x2 x3 …..xn
P p1 p2 p3 …..pn где 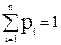 ,
,
графика или аналитически (в виде формулы) P(X=xi) = φ(xi).
Биномиальным называется закон распределения дискретной случайной величины X – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления этого события равна p. В этом случае вероятность каждого из возможных значений X = m (числа появлений сбытия) вычисляется по формуле Бернулли: Pn(m) = Cnmpmqn-m
Закон распределения Пуассона Pn(k) ≈ 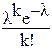 , где k - число появлений события в n независимых испытаниях, λ = np и p<<1, применяют в тех случаях, когда число испытаний велико, а вероятность p – мала.
, где k - число появлений события в n независимых испытаниях, λ = np и p<<1, применяют в тех случаях, когда число испытаний велико, а вероятность p – мала.
Математическое ожидание случайной величины:
M(X) = x1p1 + x2p2 + …. + xnpn = 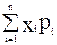
Свойства математического ожидания:
1) М(С) = С; 2) М(СХ) = С.М(Х);
3) М(Х1Х2….Хn) = М(Х1)М(Х2)…М(Хn);
4) М(Х1+Х2+ +Хn) = М(Х1) + М(Х2) +….+ М(Хn).
Математическое ожидание случайной величины Х, с биномиальным законом распределения, равно: М(Х) = np
Математическое ожидание случайной величины Х, с законом распределения Пуассона, равно: М(Х) = λ
Дисперсия случайной величины:
D(X) = M[X – M(X)]2 = M(X2) – [M(X)]2 = 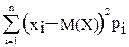
Средним квадратичным отклонением называется корень из дисперсии:
σ(X) = 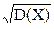
Дисперсия имеет следующие свойства:
1) D(C) = 0; 2) D(CX) = C2D(X);
3) D(Х1+Х2+ +Хn) = D(Х1) + D(Х2) +….+ D(Хn).
Дисперсия биноминального распределения равна: D(X) = npq.
Дисперсия распределения Пуассона равна: D(X) = λ.
ЗАДАЧИ
Пример 8. Устройство состоит из трех независимых элементов. Вероятность отказа каждого из них за время Т равна 0.1. Составить закон распределения числа отказавших элементов за время Т.
Решение: Дискретная случайная величина Х (число элементов, отказавших за время Т) имеет следующие возможные значения: х1 =0 (ни один из элементов не отказал), х2=1, х3=2, х4=3. Отказы элементов независимы, а их вероятности равны, следовательно, применима формула Бернулли. По условию n=3, p=0.1, получим: P3(0) = q3 = (1-p)3 = 0.93 = 0.729; P3(1) = C31pq2 = 3.0.1.0.92 = 0.243;
P3(2) = C32p2q = 3.0.12.0.9 = 0.027; P3(3) = p3 = 0.13 = 0.001
Проверим: 0.729 + 0.243 + 0.027 + 0.001 = 1.
Напишем искомый закон распределения случайной величины Х:
Х 0 1 2 3
Р 0.729 0..243 0.027 0.001
Пример 9. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения:
Х -5 2 3 4
Р 0.4 0.3 0.1 0.2
Решение: Найдем математическое ожидание М(Х) = 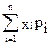
М(Х) = -5.0.4+2.0.3+3.0.1+4.0.2 = -0.3.
Теперь дисперсию D(X) = 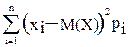
D(X) = (-5-(-0.3))2.0.4+(2-(-0.3))2.0.3 + (3-(-0.3))2.0.1 + (4-(-0.3))2.0.2 = 15.21
Наконец σ(X) = 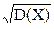 = 3.9
= 3.9
Вопросы для самопроверки
1.Что такое частота случайного события? Как частота связана с вероятностью?
2. Какие значения может принимать вероятность случайного события?
3. Какие события называют достоверными? Чему равна вероятность достоверных событий?
4. Какие события называют невозможными? Чему равна вероятность невозможного события?
5. Приведите примеры невозможных и достоверных случайных событий.
6.. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекают 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными. (Отв. 24/91)
7. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей нет бракованных. (Отв.0,65)
8. Приведите примеры маловероятных событий. Подумайте, какими из них можно, а какими нельзя пренебрегать в одном испытании.
9. Укажите, какие из перечисленных событий, по вашему мнению, являются достоверными, а какие — невозможными:
а) монета, брошенная на гладкую жесткую поверхность, встала на ребро;
б) на игральном кубике кости выпало 7 очков;
в) на игральном кубике выпало от одного до шести очков;
г) номер открытой страницы в книге — дробное число;
10. Являются ли достоверными события:
а) на игральной кости выпало четное число очков;
б) на игральной кости выпало целое число очков?
11. Вычислить: А104; Р4; С104.
12. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекают 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными. (Отв. 24/91)
13. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей нет бракованных. (Отв.0,65)
14. Составить закон распределения дискретной случайной величины Х – числа появлений «герба» при двух бросаниях монеты.
15. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения: а) Х -4 6 10; б) Х 0.21 0.54 0.61
Р 0.2 0.3 0.5 Р 0.1 0.5 0.4
Вопросы и упражнения для самопроверки:
- Дайте определение комплексного числа.
- Дайте определение мнимй единицы.
- Как найти степень мнимой единицы?
- Какие комплексные числа называются равными, сопряжеными?
- Как изображаются комплексные числа геометрически?
- Дайте определение модуля и аргумента комплексного числа.
- Перечислите формы записи комплексного числа.
- Как выполняются действия над комплексными числами, заданными в алгебраической форме; в тригонометрической форме; в показательной форме?
- Найдите модульи аргумент комплексного числа z=-2+2ί√3.Комплексное число, изображенное точкой (2, -2), запишите во всех трех формах.
- Запишите в тригонометрической форме комплексные числа: а) z=-√3+ί; б) z=-1+ί√3.
- Представьте в показательной форме комплексные числа: а) z=-√2-ί√2; б) z=5ί.
Задания контрольной работы.
Вычислить предел функции.
| 1. | 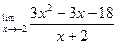
| 14. | 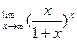
|
| 2. | 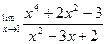
| 15. | 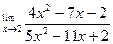
|
| 3. | 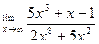
| 16. | 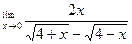
|
| 4. | 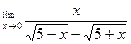
|
| |
| 5. | 
| ||
| 6. | 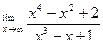
| ||
| 7. | 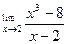
| ||
| 8. | 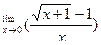
| ||
| 9. | 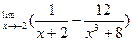
| ||
| 10. | 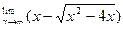
| ||
| 11. | 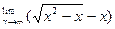
| ||
| 12. | 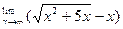
| ||
| 13. | 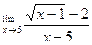
| ||
17.Решить уравнение.
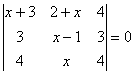 .
.
18- 21.Решить систему методом Крамера:
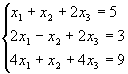
19.
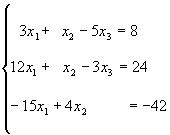
20.

3х +2y + z =3
5x - 2y - 2z = 3
x + y - z = -2
21.

5х +8y + z = 2
3x - 2y + 6z = -7
2 x + y - z = -5
22.Решить систему матричным способом
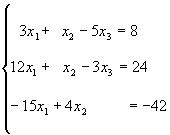
23.Решите систему уравнений при различных значениях параметра p: 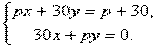
24.Решить систему уравнений, составив матричное уравнение.

3х +2y + z =3
5x - 2y - 2z = 3
x + y - z = -2
25. Решить систему уравнений методом Гаусса.

5х +8y + z = 2
3x - 2y + 6z = -7
2 x + y - z = -5
Дата: 2019-03-05, просмотров: 447.