| 1. | ∫ dx = x + C | 7. | 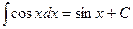
|
| 2. | ∫ xndx = 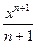 + С (п ≠ - 1) + С (п ≠ - 1)
| 8. | 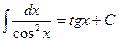
|
| 3. | ∫ x-1dx = 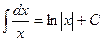
| 9. | 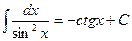
|
| 4. | 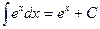
| 10. | 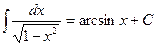
|
| 5. | 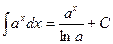
| 11. | 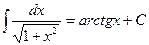
|
| 6. | 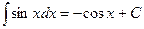
|
Если интеграл затруднительно привести к табличному с помощью элементарных преобразований, то в этом случае пользуются методом подстановки.
Пример 1. Найти 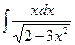
Решение. Произведем подстановку 2 - Зх2 = t ; тогда -6 xdx = dt , xdx = -(1/6) dt . Далее, получаем
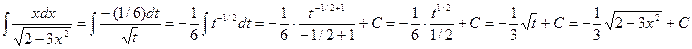
Пример 2. Найти 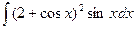
Решение. Сначала положим 2 + cos x = t; тогда 10dx = dt, откуда dx = (1/10) dt.
Далее получаем
Вопросы и упражнения для самопроверки:
1. Какое действие называется интегрированием?
2. Какая функция называется первообразной для функции f (х)?
3. Дайте определение неопределенного интеграла.
4. Перечислите основные свойства неопределенного интеграла.
5. Каким действием можно проверить интегрирование?
6. Напишите основные формулы интегрирования (табличные интегралы).
7. Найдите интегралы: a ) 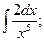 б)
б) 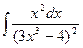
Определенный интеграл.
По данной теме сначала изучите §7-10 (1, 2), 11 (1, 2) гл. 3, §12, 14 (1 - 3) гл. 4 [3] или § 1 - 14 гл. 8 [4]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [3] гл. 3 §10 №3.5-3.8, 3.12, гл. 4 §12 № 4.1, §14 №4.3 - 4.29 или [4], гл. 8 №1-5, 8-13, 17-21, 23-27, 42-49, 50-55, 60-63.
Из контрольной работы выполните задание с 76 по 88 своего варианта.
Понятие определенного интеграла. Непосредственное вычисление определенного интеграла производится по формуле Ньютона—Лейбница;
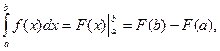
где a - нижний предел, b - верхний предел, F ( x ) - какая-нибудь первообразная функции f ( x ).
Из этой формулы виден порядок вычисления определенного интеграла:
1) Находят одну из первообразных F ( x ) данной функции;
2) Находят значения F ( x ) при x = a и x = b;
3) Вычисляют разность F ( b ) – F ( a ).
Пример 1. Вычислить интеграл 
Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:
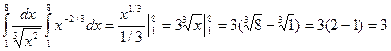
Приведем основные свойства определенного интеграла.
1. Перестановка пределов интеграла знак интеграла меняется на противоположный:
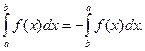
2. Отрезок интегрирования можно разбивать на части:
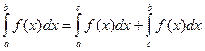
3. Постоянный множитель можно выносить за знак интеграла:
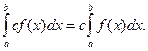
4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых:
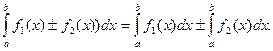
Пример 2. Вычислить интеграл 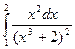
Решение.
1) Произведем подстановку x3 + 2 = t; тогда 3x3dx = dt, x2dx = 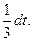
2) Определим пределы интегрирования для переменной t. При x = 1 получаем tн = 13+2 = 3, при x = 2 получаем tв = 23 + 2 = 10.
3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим:
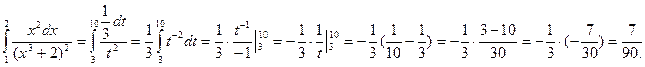
Пример 3. Вычислить интеграл 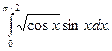
Решение.
1) Положим cos x = t ; тогда - sin xdx = dt и sin xdx = - dt ;
2) Определим пределы интегрирования для переменной t : tH = cos 0 = tH = cos (π/2) = 0.
3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим:
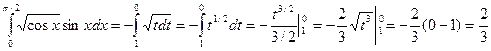
Вопросы и упражнения для самопроверки:
1. Дайте определение определенного интеграла.
2. Перечислите основные свойства определенного интеграла.
3. В чем заключается геометрический смысл определенного интеграла?
Комплексные числа
Поданной теме сначала изучите § 1—9 гл: 9 [3]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Самостоятельно закончите решение некоторых примеров. Из контрольной работы выполните задание с 89 по 96 своего варианта.
Основные понятия и определения. Решение многих задач сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов математики. Стремление сделать уравнения разрешимыми - одна из главных причин расширения понятия числа.
Так, для разрешимости уравнения х + а = b положительных чисел недостаточно и приходится вводить отрицательные числа и нуль.
Для решения уравнения ах =b (а≠О) недостаточно целых чисел и приходится вводить дробные числа. Целые и дробные числа образуют множество Q рациональных чисел.
На множестве рациональных чисел разрешимы уравнения вида ах =b (а≠О), однако уравнение х2=2 не имеет рациональных корней. Необходимость решения таких уравнений явилась одной из причин введения иррациональных чисел.
Рациональные и иррациональные числа образуют множество R действительных чисел.
Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, уравнение x2+1=0 не имеет действительных корней. Поэтому приходится расширять множество действительных чисел до нового множества; такого, чтобы в этом множестве уравнения вида x2 +a2 =0 имели решения.
Корень уравнения x2+1=0 или x2-1=0 называется мнимой единицей и обозначается буквой ί
Таким образом, символ ί удовлетворяет условию ί2= -1.
Комплексным числом называется выражение вида α+bί , где а и b— действительные числа, а ί—мнимая единица.
Число а называется действительной частью комплексного числа, а число bί — мнимой частью.
Комплексное число часто обозначают одной буквой z. Множество комплексных чисел принято обозначать буквой С.
Запись комплексного числа в виде z =a +bί называется алгебраической формой записи комплексного числа. Два комплексных числа a1+ b1ί и a2+b2 ί называются равными тогда и только тогда, когда а1 = а2 и b1=b2, т. е. когда равны их действительные части и коэффициенты при мнимой части.
Понятия «больше» и «меньше» для комплексных чисел не определяются.
Комплексное число z = 0+ называется нулем и обозначается .0; комплексное число z=a+Qί отождествляется с действительным числом . а, т. е. комплексное число z = 0 +bί называется чисто мнимым и обозначается bί, т, е. 0+bί = bί
Число ί является единственным числом, которое одновременно и действительное, и чисто мнимое.
Комплексные числа a+bί и a- bί называются сопряженными.
Действия над комплексными числами в алгебраической форме.
Суммой двух комплексных чисел z 1= a + bί и z2= c +dί. называется комплексное число
z1 +z2= (a + c) + (b + d)ί.
Умножение двух комплексных чисел выполняется по правилу:
(a + bί)(c + dί) = (aс + bd) + (ad + db)ί.
Вычитание комплексных чисел вводится как операция, обратная сложению; деление комплексных чисел вводится как операция, обратная умножению.
Правила вычитания и деления комплексных чисел z1= a + bί и z2 = c +dί определяется формулами
z2-z1= (a + bί) – (c + dί) = (a – c) + (b – d)ί.
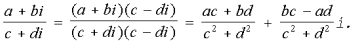
Формула теряет смысл, если c + dί = 0, так как тогда c2 + d2 = 0, т. е. деление на нуль и во множестве комплексных чисел исключается.
Формулы, определяющие правила действий над комплексными числами в алгебраической форме, не нуждаются в запоминании.
Формулы суммы, разности и произведения комплексных чисел получаются автоматически, если формально выполнить соответствующие действия над двучленами a + bί и c +dί и заменить ί2 на —1.
Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю.
Возведение комплексного числа в степень производится по формулам возведения двучлена в степень, но при этом надо, учитывать, что:
ί 1 = ί ί4 n +1 = ί1= ί
ί2 = -1 ί4n+2= ί2 = -1
ί3 = -ί ί4n+3= ί3 = - ί
ί4 = 1 ί4n = 1.
Пример 1. Найти сумму комплексных чисел z1=(2 + 3ί) и z2= (5 + ί) :
Сумму находим формальным сложением двучленов
(2 + 3ί) + (5 + ί) = (2 + 5) + (3 + 1)ί = 7 + 4ί;
Пример 2.Найти разность комплексных чисел z1=5 – 8ί и z2= 2 + 3ί :
Разность находим формальным вычитанием двучленов (5 – 8ί) – (2 + 3ί) = (3 – 2) + (– 8 – 3)ί = 1–11ί;
Пример 3.Найти произведение комплексных чисел z1= -1 + 3ί и z2= 2 + 5ί :
Произведение находим формальным перемножением двучленов (– 1 + 3ί)(2 + 5ί) = – 2 – 5ί + 6ί + 15ί2 = – 2 – 5ί + 6ί – 15 = – 17 + ί;
Пример 4. Найти произведение комплексных чисел z1= 2 + 3ί и z2= 2 - 3ί :
(2 + 3ί)(2 – 3ί) = 4 – 6ί + 6ί – 9ί2 = 4 + 9 = 13.
Из четвертого примера следует, что результатом сложения, вычитания, произведения двух комплексных чисел может быть число действительное. В частности, при умножении двух сопряженных комплексных чисел a + bί и a – bί, в результате получается действительное число, равное сумме квадратов действительной части и коэффициента при мнимой части. Произведение двух чисто мнимых чисел – действительное число. Например: 5ί•3ί= 15ί2 = – 15; – 2ί•3ί= – 6ί2 = 6.
Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю.
Например,
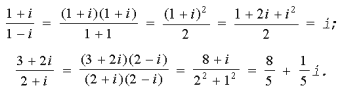
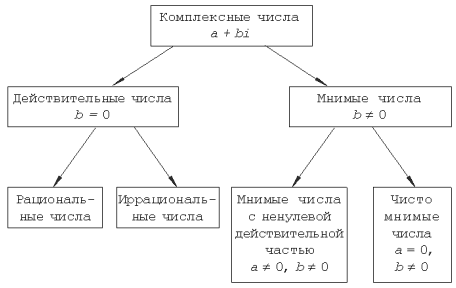
Опираясь на введенные определения нетрудно проверить, что для комплексных чисел справедливы коммутативный, ассоциативный и дистрибудивный законы. Кроме того, применение операций сложения, умножения, вычитания и деления к двум комплексным числам снова приводит к комплексным числам.Приведем классификацию комплексных чисел:
Геометрическая  интерпретация комплексных чисел
интерпретация комплексных чисел
Известно, что отрицательные числа были введены в связи с решением линейных уравнений с одной переменной. В конкретных задачах отрицательный ответ истолковывался как значение направленной величины (положительные и отрицательные температуры, передвижения в противоположных направлениях, прибыль и долг и т.п.). Однако еще в ХVI веке многие математики не признавали отрицательных чисел. Только с введением координатной прямой и координатной плоскости отчетливо проявился смысл отрицательных чисел, и они стали такими же «равноправными» и понятными, как и натуральные числа. Аналогично обстоит дело с комплексными числами. Смысл их отчетливо проявляется при введении их геометрической интерпретации.
Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу z = x + yi ставится в соответствие точка (x, y) координатной плоскости таким образом, что действительная часть комплексного числа представляет собой  абсциссу, а коэффициент при мнимой части – ординату точки.
абсциссу, а коэффициент при мнимой части – ординату точки.
Таким образом, устанавливается взаимно однозначное соответствие между множеством комплексных чисел и множеством точек координатной плоскости. Подобным образом было установлено соответствие между множеством действительных чисел и множеством точек числовой прямой.
На рисунке 1 изображена координатная плоскость. Числу 2 + 3i соответствует точка A(2, 3) плоскости; числу 2 – 3i – точка B(2, – 3); числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка D(– 2; – 3). Числу 3i соответствует точка E(0, 3); а числу – 3i – точка F(0, – 3). Итак, каждому комплексному числу соответствует единственная точка координатной плоскости и, обратно, каждой точке координатной плоскости соответствует единственное комплексное число, при этом двум различным комплексным числам соответствуют две различные точки координатной плоскости. Ясно, что действительным числам x + 0i соответствуют точки оси абсцисс, а чисто мнимым числам 0 + yi точки оси ординат. Поэтому ось Oy называют мнимой, а ось Ox – действительной. Сопряженным комплексным числам 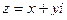 и
и 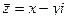 соответствуют точки, симметричные относительно оси абсцисс (рис. 2).
соответствуют точки, симметричные относительно оси абсцисс (рис. 2).
Тригонометрическая форма комплексного числа
 Точка координатной плоскости, соответствующая комплексному числу z = x + yί, может быть указана по-другому: ее координатами могут быть расстояние r от начала координат и величина угла φ между положительной полуосью Ox и лучом Oz (рис. 3).
Точка координатной плоскости, соответствующая комплексному числу z = x + yί, может быть указана по-другому: ее координатами могут быть расстояние r от начала координат и величина угла φ между положительной полуосью Ox и лучом Oz (рис. 3).
Расстояние r от начала системы координат до точки, соответствующей комплексному числу z, называют модулем этого числа. На основании теоремы Пифагора (рис. 2) получается формула: 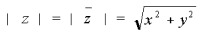
Если комплексное число z изображается точкой оси абсцисс (т.е. является действительным числом), то его модуль совпадает с абсолютным значением. Все комплексные числа, имеющие модуль 1, изображаются точками единичной окружности – окружности с центром в начале системы координат, радиуса 1 (рис. 4).
 Аргументом комплексного числа z≠ 0 называется величина угла φ между положительным направлением действительной оси и вектором, соответствующим этому числу(рис. 3).
Аргументом комплексного числа z≠ 0 называется величина угла φ между положительным направлением действительной оси и вектором, соответствующим этому числу(рис. 3).
Сопряженные комплексные числа 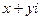 и
и 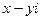 имеют один и тот же модуль
имеют один и тот же модуль 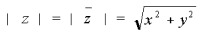 и аргументы, отличающиеся знаком: j = – j.
и аргументы, отличающиеся знаком: j = – j.
В отличие от модуля аргумент комплексного числа определяется неоднозначно. Аргумент одного и того же комплексного числа может иметь бесконечно много значений, отличающихся друг от друга на число, кратное 360°. Например, число z (рис. 3) имеет модуль r, аргумент же этого числа может принимать значения ; j + 360°; j + 720°; j + 1080°; … или значения j – 360°; j –720°; j – 1080°; … Данное значение модуля r и любое из приведенных выше значений аргумента определяют одну и ту же точку плоскости, соответствующую числу z.Пусть точке с координатами (x; y) соответствует комплексное число z = x + yi. Запишем это комплексное число через его модуль и аргумент. Воспользуемся определением тригонометрических функций синуса и косинуса (рис. 3):
x = r cos j; y = r sin j.
Тогда число z выражается через модуль и аргумент следующим образом:
z = x + yί = r(cos j + ί sin j).
Выражение z = r(cos j + ίsin j) называют тригонометрической формой комплексного числа, в отличии от выражения z = x + yi, называемого алгебраической формой комплексного числа.
Приведем примеры обращения комплексных чисел из алгебраической формы в тригонометрическую:
Для числа i имеем r = 1, j = 90°, поэтому ί = 1(cos 90° + ί sin 90°);
Для числа – 1 имеем r = 1, j = 180°, поэтому – 1 = 1(cos 180° + ί sin 180°);
Для числа 1 + ί имеем 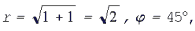 поэтому
поэтому 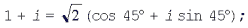
Для числа 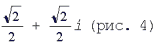 имеем r = 1, j = 45°, поэтому
имеем r = 1, j = 45°, поэтому 
Для числа 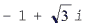 имеем r = 2, j = 120°, поэтому
имеем r = 2, j = 120°, поэтому 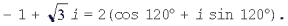
Справедливость приведенных равенств нетрудно проверить путем подстановки в их правой части числовых значений тригонометрических функций. Итак, для того, чтобы комплексное число, заданное в алгебраической форме, обратить в тригонометрическую форму, необходимо найти его модуль r и аргумент j, пользуясь формулами:
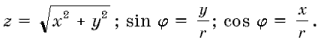
Пример 5. Представить в тригонометрической форме число 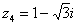
Найдем его модуль и аргумент.
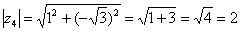
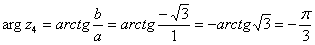
Таким образом:
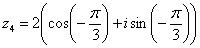 – число
– число  в тригонометрической форме.
в тригонометрической форме.
Арифметические действия над комплексными числами, заданными в тригонометрической форме, производятся следующим образом. Пусть z 1 = r 1 (cos φ 1 + i sin φ 1 ) и z 2 = r 2 (cos φ 2 + i sin φ 2 ). Имеем:
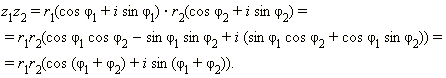
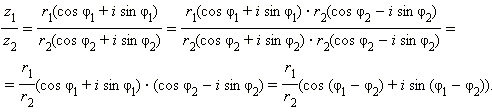 Видно, что в тригонометрической форме операции умножения и деления производятся особенно просто: для того, чтобы перемножить (разделить) два комплексных числа, нужно перемножить (разделить) их модули и сложить (вычесть) их аргументы.
Видно, что в тригонометрической форме операции умножения и деления производятся особенно просто: для того, чтобы перемножить (разделить) два комплексных числа, нужно перемножить (разделить) их модули и сложить (вычесть) их аргументы.
Для возведения в степень используется формула Муавра :
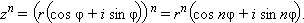
Пример 7. Представить комплексное число 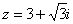 и найти
и найти 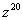 .
.
Самостоятельно представь данной число в тригонометрической форме. Вы должны получить:
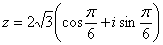
Ввоспользовавшись формулой Муавра, получим:
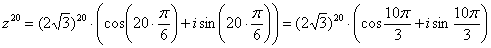
Упростим выражение. Т.к. 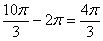 , окончательный ответ :
, окончательный ответ :
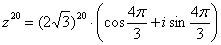 или
или
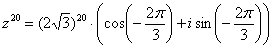
Для того, чтобы извлечь корень из произвольного комплексного числа рассмотрим уравнение 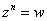 или, то же самое:
или, то же самое: 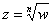 . Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при
. Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при 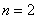 получается квадратный корень
получается квадратный корень 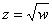
Уравнение вида 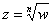 имеет ровно
имеет ровно 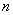 корней
корней 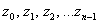 , которые можно найти по формуле:
, которые можно найти по формуле:
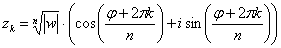 , где
, где 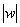 – это модуль комплексного числа
– это модуль комплексного числа 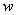 ,
, 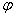 – его аргумент, а параметр
– его аргумент, а параметр 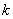 принимает значения:
принимает значения: 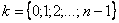
Пример 8.
Найти корни уравнения 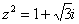
Перепишем уравнение в виде 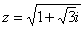
В данном примере 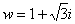 ,
, 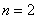 , поэтому уравнение будет иметь два корня:
, поэтому уравнение будет иметь два корня: 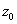 и
и 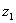 .
.
Общую формулу можно детализировать:
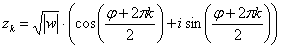 ,
, 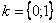
Найдем модуль и аргумент комплексного числа 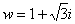 :
:
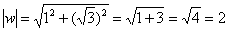
Число 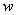 располагается в первой четверти, поэтому:
располагается в первой четверти, поэтому:
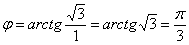
Еще более детализируем формулу:
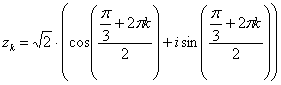 ,
, 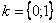
Подставляя в формулу значение 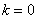 , получаем первый корень:
, получаем первый корень:
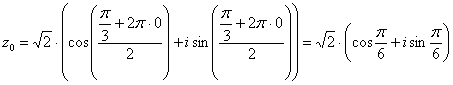
Подставляя в формулу значение 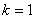 , получаем второй корень:
, получаем второй корень:
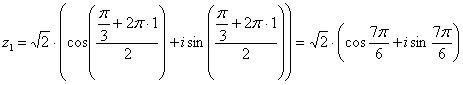
Получаем:
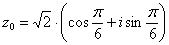 ,
, 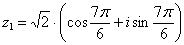
Показательная форма комплексного числа.
Рассматривая функцию y = ex для комплексного переменного Эйлер установил замечательное соотношение
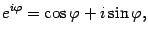
которое носит название формулы Эйлера.
Любое комплексное число (кроме нуля) 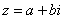 можно записать в показательной форме:
можно записать в показательной форме:
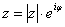 , где
, где 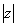 – это модуль комплексного числа, а
– это модуль комплексного числа, а 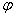 – аргумент комплексного числа.
– аргумент комплексного числа.
Для того , чтобы записать число в показательной форме необходимо найти модуль и аргумент и записать число в виде 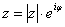 .
.
Пример 9. Число 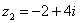 записать в показательной форме. Вычислите самостоятельно модуль и аргумент. Получаться выражения:
записать в показательной форме. Вычислите самостоятельно модуль и аргумент. Получаться выражения:
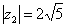 ,
, 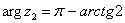 .
.
Тогда данное число в показательной форме запишется следующим образом: 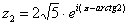 .
.
Над комплексными числами заданными в показательной форме , удобно производить умножение и деление, возведение в натуральную степень и извлечение корня.
Найдем произведение комплексных чисел 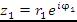 и
и 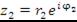 , представленных в показательной форме:
, представленных в показательной форме:
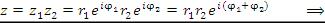
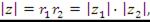
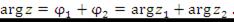
Таким образом, чтобы найти произведение комплексных чисел, нужно перемножить их модули и сложить аргументы.
Аналогично находится деление комплексных чисел 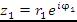 и
и 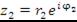 :
:
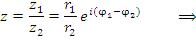
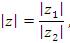
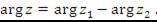
Чтобы разделить одно комплексное число на другое, нужно модуль первого числа разделить на модуль второго и из аргумента первого числа вычесть аргумент второго.
Для возведения в целую степень n комплексного числа  , это число нужно представить в показательной форме, возвести обе части полученного равенства в степень n и записать результат в тригонометрической форме:
, это число нужно представить в показательной форме, возвести обе части полученного равенства в степень n и записать результат в тригонометрической форме: 
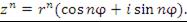
Пример 10. Представить в показательной форме комплексное число 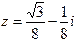 .
.
Решение. Находим модуль числа 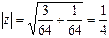 и один из его аргументов
и один из его аргументов 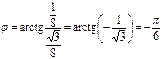
откуда, 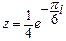 .
.
Дата: 2019-03-05, просмотров: 365.