Основные понятия комбинаторики: перестановки, размещения, сочетания и их свойства. Основные понятия теории вероятности: вероятность событий, формулы вычислений вероятностей. Основы математической статистики:

Ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Изучите Гл.16 §2.[4] или Гл.6 §18, Гл.7§20-23[ [3] Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: Гл.16 §2-6 . [4] 65,68,70 стр.282-284.Выполните задание с101-125.

Литература.

1. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. Изд.6-е, стер. - М., Высшая школа, 1998. - 479 с.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математическая статистике. Изд.2-е, доп. - М., Высшая школа, 1975. - 333 с.
3. Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию вероятностей. Изд.8-е, испр. - М., Наука, 1976. - 168 с.
4. Бунимович Е., Булычев В. Вероятность и статистика в курсе математики основной школы. Учебно-методическая газета Математика №№ 17 - 24.2007

        Определения и теоремы теории вероятностей

 Комбинаторика.Задачи, при решении которых приходится составлять различные комбинации из конечного числа элементов и производить подсчет конечного числа всех возможных таких комбинаций , называются комбинаторными.

Размещения. Пусть имеется множество, содержащее n элементов. Каждое его упорядоченное подмножество, содержащее по m элементов, называется размещением из n элементов по m элементов.

       Число размещений из n элементов по m элементов вычисляется по формуле:

                                          A_n^m = n!/(n-m)!                                                     (1.3)

       Перестановки. Размещения из n элементов n элементов называются перестановками из n элементов.

Число перестановок n элементов:

                                          P_n = n!                                                       (1.4)

   C сочетания.  Пусть имеется множество, содержащее n элементов. Каждое его подмножество, содержащее по m элементов, называется сочетанием из n элементов по m элементов.

       Число сочетаний из n элементов по m элементов вычисляется по формуле:

                   C_n^m = n!/m!(n-m)! = (m+1)(m+2)….n/(n-m)!                   (1.5)

                                          C_n^m = C_n^n-m

       Пример 1. Вычислить: А₃²; Р₂; С₃².

       Решение: А₃² = 3!/(3-2)! = 6; Р₂ = 2! = 2; С₃² = 3!/2!/(3-2)! = 3

 Случайные события. Классическое и статистическое определение вероятности

       Будем называть испытанием (опытом, наблюдением, измерением) некоторую совокупность действий. Предполагается, в общем случае, что испытание можно повторить неограниченное число раз.

Событием (случайным событием) называется всякий факт, который может произойти или не произойти в результате опыта. События обозначаются буквами А, B, C, D, …

Вероятностью события называется численная мера возможности появления события в результате данного опыта. Вероятность события А обозначается Р(А). Событие W, которое обязательно произойдет в результате опыта, называется достоверным: Р(W) = 1. Событие Æ, которое никогда не может произойти в результате опыта, называется невозможным: Р(Æ) = 0. Событие А, о котором нельзя заранее сказать произойдет оно или нет в результате опыта, называется случайным: 0£Р(А)£1.

Суммой событий А+В называется событие, состоящее в осуществлении хотя бы одного из событий А или В (безразлично, какого именно, или обоих, если это возможно).

События А и В называются несовместными, если они не могут произойти одновременно при одном и том же испытании.

 Теоремы сложения и умножения вероятностей

Вероятность появления одного из нескольких несовместных событий (безразлично какого) равна сумме вероятностей этих событий:

P(A+B+C) = P(A)+P(B)+P(C)                                                    (3.1)

Вероятность появления одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

P(A+B) = P(A)+P(B) – P(AB)                                                    (3.2)

Теорема обобщается на любое конечное число совместных событий.

Вероятность совместного появления двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

P(AB) = P(A)P_A(B)                                  (3.4)

В частности для независимых событий:

P(AB) = P(A)P(B)                                               (3.5)

т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Два случайных события называются противоположными, если появление одного из них равносильно непоявлению другого. Если одно из этих событий обозначить А, то другое (противоположное) обозначают А (читается «не А»). Событие А означает, что А не произошло: Р(А)+Р(А)=1.

Произведением двух событий АВ называется событие, состоящее в том, что оба события произошли одновременно. Если появление каждого из событий не зависит от того, произошло или нет другое, то события называются независимыми, и вероятность их произведения равна произведению вероятностей этих событий: Р(АВ)=Р(А)×Р(В).

Если вероятность появления события В изменяется в зависимости от того, произошло или нет событие А, то такие события называются зависимыми. Вероятность события В при условии, что событие А уже произошло, обозначается 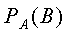. Вероятность произведения зависимых событий определяется формулой .

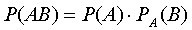Если события А и В несовместные, то Р(АВ)=0.

Формула для вычисления вероятности суммы двух событий, все равно каких, совместных или нет, имеет вид: Р(А+В)=Р(А)+Р(В)-Р(АВ).

Полной группой событий называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них.

Несколько событий в данном опыте называются равновозможными, если нет оснований считать какое-либо из них более возможным, чем другое. События 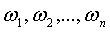называются элементарными, если они образуют полную группу событий, несовместны (то есть никакие два из них не могут произойти одновременно) и равновозможны. Если некоторое событие А происходит в результате появления одного из элементарных событий 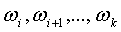, то эти элементарные события называются благоприятствующими событию А.

Классическое определение вероятности. Пусть в результате опыта может произойти одно из n элементарных событий, причем событию А благоприятствуют m из них (m£n). Тогда вероятностью события А называется отношение числа элементарных исходов, благоприятствующих появлению события А, к общему числу равновозможных элементарных исходов:

Р(А)= m/ n.

Пример 1. Из пяти букв разрезной азбуки составлено слово ДОМИК. Ребенок, не умеющий читать, рассыпал эти буквы и затем выложил три из них в произвольном порядке. Найти вероятность того, что у него получилось слово КОД. (Предполагается, что ребенок не переворачивает буквы.)

Решение. Пусть случайное событие А состоит в том, что получено слово КОД. Число равновозможных элементарных исходов равно числу размещений из 5 элементов по 3: .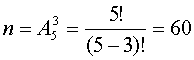

Поскольку все буквы в первоначальном слове разные, то среди 60 исходов не будет двух одинаковых, то есть слово КОД встречается только один раз: m=1, Р(А)=1/60.

В некоторых случаях не удается перечислить или посчитать все элементарные и благоприятствующие исходы. Тогда принимается какая-либо другая мера подсчета (например, площадь фигуры или объем тела). Такие вероятности называются геометрическими. Если обозначить W - пространство элементарных исходов, то можно записать .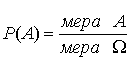

Пример 2. В круг радиуса R вписан квадрат. Из круга наудачу выбирается точка. Какова вероятность того, что эта точка лежит внутри квадрата?

Решение. Событие А состоит в том, что наудачу выбранная из круга точка оказалась лежащей внутри квадрата. Понятно, что посчитать количество точек внутри круга и внутри квадрата невозможно, поэтому мерой числа равновозможных элементарных исходов будет площадь круга 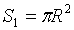, а мерой числа благоприятных исходов – площадь квадрата .

.

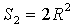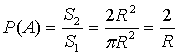Рассмотрим различные примеры решения задач с применением указанных выше формул.

Пример3.В двух ящиках содержатся синие и красные шары: в первом ящике 6 синих и 7 красных, во втором ящике – 4 синих и 5 красных. Из каждого ящика извлекают по одному шару. Найти: 1) вероятность того, что хотя бы один из вынутых шаров будет красным; 2) вероятность того, что только один из шаров будет красным.

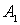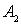Решение. Пусть событие А состоит в том, что хотя бы один их вынутых шаров красный. Обозначим за и события, состоящие в извлечении красного шара из первого и из второго ящиков соответственно. Тогда событие А будет выражено через события 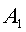и 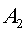формулой А= 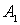+ 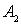, а вероятность этого события, согласно правилу нахождения вероятности суммы двух событий Р(А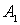)=Р( )+Р( 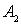) – Р( ).

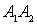События 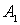и 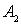- независимые, поэтому 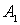Р( 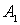)=Р( )Р( ).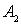

Вычислим вероятности событий. В первом ящике находится 13 шаров, из них 7 красные, следовательно Р( 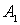)=7/13. Во втором ящике = 9 шаров, из них 5 – красные, то есть Р( 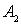)= 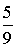. Р(А)= 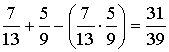. Этот же результат можно было получить, рассматривая противоположное событие`А, состоящее в том, что ни один из вынутых шаров не оказался красным: `А=` 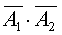, , 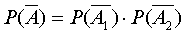Р(А)=1-Р(`А) . Подставив числовые значения 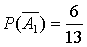, , 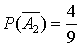получим .

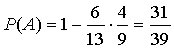Пусть событие В состоит в том, что только один из вынутых шаров оказался красным 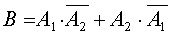. События 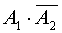и 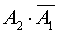несовместные, поэтому , .

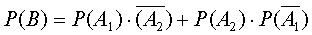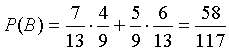Пример 4. (задача о выборке). В лотерее 10 билетов, из них 4 выигрышных. Найти вероятность того, что среди взятых наугад пяти билетов будут два выигрышных.

Решение. Пусть А – событие, состоящее в том, что среди выбранных наудачу пяти билетов оказались два выигрышных. По классическому определению вероятностей Р(А)=m/n, где n – число способов, которыми из 10 имеющихся билетов можно выбрать любые 5 все равно в каком порядке: n=. Число благоприятных исходов m равно числу способов, которыми можно выбрать два выигрышных билета из четырех имеющихся и еще три невыигрышных билета из шести: m=Р(А).

    Пример 5. Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях: – а) четная (событие А), б) причем на грани хотя бы одной из костей окажется четверка (событие В).

       Решение.  На выпавшей грани «первой» кости может появиться одно, два, три,…..шесть очков и все эти события равновероятны, в силу симметричности кости. Очевидно, что те же шесть элементарных исходов возможны и при бросании «второй» кости. Легко видеть, что каждый из исходов бросания «первой» кости может сочетаться с каждым из исходов бросания «второй». Отсюда следует, что общее число возможных исходов испытания (бросание двух костей) равно 6^.6 = 36. Все эти исходы равновероятны.

       а) Благоприятными для интересующего нас события А (сумма очков на гранях четная) являются следующие восемнадцать исходов (первым написано число очков на «первой» кости, вторым число очков на «второй» кости; далее дана их сумма):

1) 1,1; 1+1=2, 2) 1, 3; 1+3=4, 3) 1,5; 1+5=6, 4) 2,2; 2+2=4, 5) 2,4; 2+4=6,

6) 2,6; 2+6=8, 7) 3,1; 3+1=4, 8) 3,3; 3+3=6, 9) 3,5; 3+5=8, 10) 4,2; 4+2=6,

11) 4,4; 4+4=8, 12) 4,6; 4+6=10, 13) 5,1; 5+1=6, 14) 5,3; 5+3=8, 15) 5,5; 5+5=10,

16) 6,2; 6+2=8, 17) 6,4; 6+4=10, 18) 6,6; 6+6=12.

       Вероятность того, что сумма очков, выпавших на гранях двух костей, число четное, равна отношению числа благоприятных исходов к полному числу элементарных исходов испытания: Р(А) = 18/36 = 1/2.

       б) В этом случае из всего множества исходов благоприятных для события А, только пять окажутся и благоприятными и для события В (сумма очков четная, причем на грани хотя бы одной из костей окажется четверка):

1) 2,4; 2+4=6, 2) 4,2; 4+2=6, 3) 4,4; 4+4=8, 4) 4,6; 4+6=10, 5) 6,4; 6+4=10,

       Искомая вероятность Р(В) = 5/36.

Пример 6. При перевозке ящика, в котором находились 21 стандартная деталь и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Наудачу извлеченная (после перевозки) из ящика деталь оказалась стандартной. Найти вероятность того, что была утеряна: а) стандартная деталь (событие А); б) нестандартная деталь (событие В).

Решение.

а) Извлеченная стандартная деталь не могла быть утеряна, и значит утеряна одна из остальных 30 деталей (21 + 10 – 1 = 30). Среди них было 20 стандартных (21 – 1 = 20) и 10 нестандартных. Следовательно вероятность события А: Р(А) = 20/30 = 2/3.

б) Легко сообразить, что события А и В противоположны (утеряна либо стандартная, либо нестандартная деталь). Следовательно P(B) = 1-P(A) = 1/3.

5.1.3.1. На стеллаже в случайном порядке расставлены 15 учебников, причем 5 из них по теории вероятностей (ТВ). Наудачу берут три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется по ТВ (событие А).

       Решение. Способ 1. Событие А будет реализовано, если произойдет одно из следующих трех несовместных событий:

В – только один из взятых учебников по ТВ;

С – два из трех учебников по ТВ; D – все три учебника по ТВ.

Интересующее нас событие А есть сумма А=В+С+D и по теореме сложения вероятностей получим P(A) = P(B)+P(C)+ P(D)                                         

       Найдем вероятности событий В, С и D (см. решение задачи 5.1.1.18):

P(B) = C₅^1.C₁₀²/C₁₅³ = 45/91; P(C) = C₅^2.C₁₀¹/C₁₅³ = 20/91; P(D) = C₅³/C₁₅³; = 2/91.

       Теперь подставим их в выражение для вероятности события А:

P(A) = 45/91 + 20/91 + 2/91 = 67/91

Пример 7. Для сигнализации об утечке ядовитого газа установлены два независимо работающих датчика. Вероятность срабатывания первого из них Р(А) = 0.95, а второго – Р(В) = 0.9. Найти вероятность срабатывания при аварии: а) хотя бы одного датчика; б) только одного датчика.

Решение:

а) Очевидно, что срабатывания датчиков события совместные. Тогда вероятность срабатывания хотя бы одного датчика (событие С) Р(С) = Р(А+В) и Р(А+В) = Р(А)+Р(В) – Р(АВ); Р(АВ) = Р(А)^.Р(В) = 0.885; Р(С) = 0.95 + 0.9 – 0.885 = 0.995.

б) Пусть событие D означает срабатывание только одного, любого, датчика, тогда 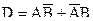 Причем события  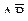и 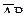 несовместные. Следовательно, по теореме сложения вероятностей имеем:  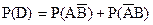и, применив теорему умножения вероятностей для независимых событий (срабатывания первого и второго датчиков события независимые), получим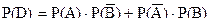 = 0.95^.0.1 + 0.9^.0.05 = 0.14.