По данной теме изучите §27-30 гл. 6 [2] или §1-17 гл. 5 [3]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [2] гл. 6 §30 № 6.25 - 6.49 (нечетные) или [4] гл. 5 № 11 - 31, 36 - 39, 67, 71 (1-5).
Из контрольной работы выполните задание с 25-50 своего варианта.
Производная. Понятие производной является одним из важнейших в курсе математики. Многие задачи, как самой математики, так и естествознания и техники приводят к этому понятию.
Производная функции y = f(x) в точке x называется предел отношения приращения функции к приращению аргумента, когда последнее стремиться к нулю:
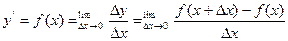
Функция, имеющая конечную производную, называется дифференцируемой. Операция нахождения производной называется дифференцированием.
Если y = f ( u ) и u = φ( x ) – дифференцируемые функции своих аргументов, то производная сложной функции y = f (φ( x )) существует и равна произведению производной функции y по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной x:
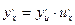
Аналогичная формула верна и для сложных функций, которые задаются с помощью цепочки, содержащей три звена и более.
Таблица формул дифференцирования.
| 1. | c’ = 0 | 12. | (ln u)’ = 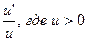
|
| 2. | x’ = 1 | 13. | (logau)’ = 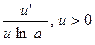
|
| 3. | (u ± v)’ = u’ ± v’ | 14. | (sin u)’ = cos u ∙ u’ |
| 4. | (uv)’ = uv’ + vu’ | 15. | (cos u)’ = - sin u ∙ u’ |
| 5. | (cu)’ = cu | 16. | (tg u)’ = 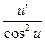 = sec2 u ∙ u’ = sec2 u ∙ u’
|
| 6. | 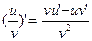
| 17. | (ctg u)’ = - 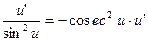
|
| 7. | 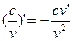
| 18. | (arcsin u)’ = 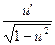
|
| 8. | (un)’ = nun-1 u’ | 19. | (arccos u)’ = - 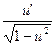
|
| 9. | 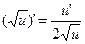
| 20. | (arctg u)’ = 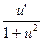
|
| 10. | (au)’ = au ln a ∙ u’ | 21. | (arcctg u)’ = - 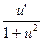
|
| 11. | (eu)’ = eu ln eu’ = euu’ |
Здесь u и v – дифференцируемые функции от x, а с – постоянная величина.
Пример 1 . Найти производную функции f(x) = 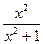
Решение. Дифференцируем функцию по формулам 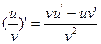 (un) = nun-1u’:
(un) = nun-1u’:
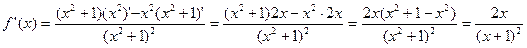
Пример 2. Найти производную функции y = sin3φ и вычислить ее значение при φ = π/3.
Решение. Это сложная функция с промежуточным аргументом sinφ. Дифференцируем ее по формулам (un)’ = nun-1 u’ , (sin u)’ = cos u ∙ u’:
f’(φ) = 3sin2φ (sinφ)’ = 3sin2φ cosφ
Вычислим значение производной при φ = π/3:
f’ (π/3) = 3 sin2 (π/3) cos (π/3) = 3 ( 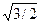 )2∙ (1/2) = 3 ∙ (3/4) ∙ (1/2) = 9/8
)2∙ (1/2) = 3 ∙ (3/4) ∙ (1/2) = 9/8
Пример 3. Найти производную функции f(x) = ln 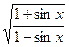
Решение. Сначала преобразуем функцию, используя свойства логарифмов:
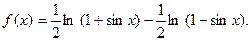
Дифференцируя, получим:
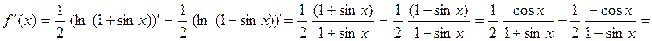
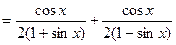

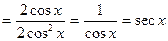
Приложение производной к исследованию функций.
Дифференцируемая функция y = f ( x ) возрастает на промежутке ] a, b [, если ее производная положительна в каждой точке этого промежутка.
Дифференцируемая функция y = f ( x ) убывает на промежутке ] a, b [, если ее производная отрицательна в каждой точке этого промежутка.
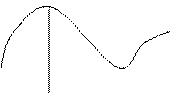
Функция y = f ( x ) имеет максимум в точке x = x 1 (рис. 1), если для всех значений х, достаточно близких к х1, выполняется неравенство f (х) < f (х1); x = x 1 - точка максимума; ymax = f (х1) - максимум функции.
Функция y = f ( x ) имеет минимум в точке х = x 2 (рис. 1), если для всех значений х, достаточно близких к x 2 , выполняется неравенство f ( x ) > f (х2); х = x 2 - точка минимума; ymin = f ( x 2 ) - минимум функции.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - экстремальными.
Точки, в которых производная функции обращается в нуль, называются критическими точками I рода.
y 
 |
y = f(x)
f(x1)
 f(x2)
f(x2)
0  x1 x2 x
x1 x2 x
рис. 1
Первое достаточное условие существования экстремума функции. Если при переходе через критическую точку I рода х = х0 производная функции у = f (х) меняет знак, то х = х0 - точка экстремума.
При этом если производная меняет знак с плюса на минус, то х = х0 - точка максимума, a ymax = f ( x 0 ). Если же производная меняет знак с минуса на плюс, то х = х0 - точка минимума, a ymin = f ( x 0 ).
Второе достаточное условие существования экстремума функции. Если в точке х = х0 первая производная функции у = f (х) обращается в нуль, а вторая производная отлична от нуля, то х = х0 - точка экстремума.
При этом если вторая производная в этой точке положительна (f’’(x0) > 0), то х = х0 - точка минимума; если вторая производная в этой точке отрицательна ( f "( x 0 ) < 0), то х = х0 - точка максимума.
Направление вогнутости и точки перегиба кривой. Говорят, что на промежутке ] а, b [ кривая обращена выпуклостью вверх или выпукла ( 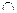 ), если она лежит ниже касательной, проведенной в любой ее точке (рис. 2).
), если она лежит ниже касательной, проведенной в любой ее точке (рис. 2).
y Говорят, что кривая на промежутке ] b, с [ обращена
 выпуклая выпуклостью вниз или вогнута (
выпуклая выпуклостью вниз или вогнута (  ), если она лежит выше
), если она лежит выше

 y = f ( x ) касательной, проведенной в любой ее точке (рис. 2).
y = f ( x ) касательной, проведенной в любой ее точке (рис. 2).
Точка А, в которой меняется направление вогнутости кривой,
А называется точкой перегиба кривой (рис. 2).
График дифференцируемой функции у = f(x) является
 выпуклым на промежутке ] а; b [ если вторая производная
выпуклым на промежутке ] а; b [ если вторая производная
вогнутая функции отрицательна в каждой точке этого промежутка.
 a b c x График дифференцируемой функции у = f ( x ) является
a b c x График дифференцируемой функции у = f ( x ) является
рис. 2 вогнутым на промежутке ] b; с [, если вторая производная функции положительна в каждой точке этого промежутка.
Точки, в которых вторая производная функции обращается в нуль, называются критическими точками II рода.
Если при переходе через критическую точку II рода х = x0 вторая производная функция меняет знак, то х = х0 - абсцисса точки перегиба. Ордината точки перегиба равна значению функции в точке х0, т. е. ут п = f(x0); А(х0; f ( x 0 )) - точка перегиба графика функции у = f (х).
Исследование функций и построение их графиков. Исследование функции можно проводить по следующей схеме:
1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями координат.
3. Найти промежутки монотонности и экстремумы функции.
4. Найти направление вогнутости и точки перегиба графика функции.
5. Для уточнения графика функции рекомендуется найти несколько дополнительных точек из уравнения функции.
Пример. Построить график функции у = х3 - 6x2 + 9x - 3.
1. Функция определена на всей числовой прямой, т. е. D(y) = R.
2. Данная функция не является ни четной, ни нечетной; кроме того, она не является периодической.
3. Найдем точку пересечения графика с осью Оу: полагая х = 0, получим y = -3. Точки пересечения графика с осью Ох в данном случае найти затруднительно.
4. Очевидно, что график функции не имеет асимптот.
5.  Найдем производную: у' = 3х2 - 12х + 9. Далее, имеем (Зх2 - 12х + 9 = 0) <=> (х2 - 4х + 3 = 0) <=>
Найдем производную: у' = 3х2 - 12х + 9. Далее, имеем (Зх2 - 12х + 9 = 0) <=> (х2 - 4х + 3 = 0) <=> 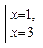 Точки х=1 и х = 3 делят область определения функции на три промежутка: - ∞ ,1 [,
Точки х=1 и х = 3 делят область определения функции на три промежутка: - ∞ ,1 [,

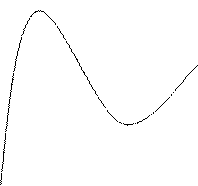 y (1;1) ] 1,3 [ и ] 3, + ∞ [ В промежутках ] - ∞, 1 [и] 3, + ∞ [ у' > 0, т е.
y (1;1) ] 1,3 [ и ] 3, + ∞ [ В промежутках ] - ∞, 1 [и] 3, + ∞ [ у' > 0, т е.
функция возрастает, а в промежутке ] 1, 3 [ y '< 0 т. е. функция
 убывает.
убывает.
0 x При переходе через точку х = 1 производная меняет знак с
плюса на минус, а при переходе через точку х = 3 - с минуса на
(2;1) плюс. Значит, ymax = y(1) =1, ymin = y(3) = -3
6. Найдем вторую производную: у" = 6х - 12; 6 x - 12 = 0, x =
(0;-3) (3;-3) = 2. Точка х = 2 делит область определения функции на два
промежутка ] - ∞, 2[ и ]2, + ∞[. В первом из них у" < 0, а во
втором у" > 0, т. е. в промежутке ] - ∞, 2[ кривая выпукла
рис. 3 вверх, а в промежутке ]2, + ∞[ выпукла вниз.
Таким образом, получаем точку перегиба (2; -1).
7. Используя полученные данные, строим искомый график (рис. 3).
Интегральное исчисление
Неопределенный интеграл и его свойства. Непосредственное интегрирование. Определенный интеграл. Вычисление и свойства определенного интеграла. Применение определенного интеграла.
По данной теме сначала изучите §7-10 (1, 2), 11 (1, 2) гл. 3, §12, 14 (1 - 3) гл. 4 [3] или § 1 - 14 гл. 8 [4]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Запишите таблицу интегралов. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [3] гл. 3 §10 №3.5-3.8, 3.12, гл. 4 §12 № 4.1, §14 №4.3 - 4.29 или [4], гл. 8 №1-5, 8-13, 17-21, 23-27, 42-49, 50-55, 60-63.
Из контрольной работы выполните задания с 51 по 75 своего варианта.
Литература.
1. «Алгебра и начало анализа», под ред. Г.Н. Яковлева, М.: 1981 г. ч. I.
2. «Алгебра и начало анализа», под ред. Г.Н. Яковлева, М.: 1981 г. ч. II.
3. И.И. Валуцэ, Г.Д. Дилигул «Математика для техникумов», М.: Просвещение, 2005 г.
4. Н.В. Богомолов «Практические занятия по математике», М.: Просвещение, 2005 г.
Неопределенный интеграл.
Понятие неопределенного интеграла. Дифференцирование - это действие, с помощью которого по данной функции находится ее производная или дифференциал. Например, если F(x ) = x 10 , то F ' (х) = 10х9, dF (х) = 10х9 d х.
Интегрирование - это действие, обратное дифференцированию. С помощью интегрирования по данной производной или дифференциалу функции находится сама функция. Например, если F ' х = 7 x 6 , то F (х) = х7 , так как (х7)’ = 7х6 .
Дифференцируемая функция F ( x ), x 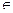 ]a b[ называется первообразной для функции f (х) на интервале ]a; b[, если F '( x ) = f ( x ) для каждого х
]a b[ называется первообразной для функции f (х) на интервале ]a; b[, если F '( x ) = f ( x ) для каждого х 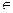 ] а; b [.
] а; b [.
Так, для функции f { x ) = 1/cos2 х первообразной служит функция F (х) = tg х, поскольку (tg x)'= = 1/cos2 x.
Совокупность всех первообразных функций f ( x ) на интервале ]а; b[ называют неопределенным интегралом от функции f ( x ) на этом интервале и пишут 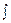 f ( x ) dx = F ( x ) + С. Здесь f ( x ) dx -подынтегральное выражение; f ( x )- подынтегральная функция; х - переменная интегрирования; С - произвольная постоянная.
f ( x ) dx = F ( x ) + С. Здесь f ( x ) dx -подынтегральное выражение; f ( x )- подынтегральная функция; х - переменная интегрирования; С - произвольная постоянная.
Например, 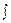 5x ’ dx = х5 + С, так как (x5 + С)' = 5х1.
5x ’ dx = х5 + С, так как (x5 + С)' = 5х1.
Приведем основные свойства неопределенного интеграла.
1. Дифференциал неопределенного интеграла равен подынтегральному выражению:
d 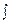 f ( x ) dx = f ( x ) dx .
f ( x ) dx = f ( x ) dx .
2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т. е.
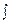 dF ( x ) = F ( x + C .
dF ( x ) = F ( x + C .
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
∫ af(x) dx = a ∫ f(x)dx.
4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от каждой функции:
∫ ( f 1 (х) ± f 2 (x)) dx = ∫ f 1 (х) dx ± ∫ f 2 ( x ) dx .
Дата: 2019-03-05, просмотров: 319.