Системой однородных линейных уравнений называется система вида
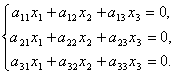
Ясно, что в этой случае 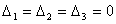 , т.к. все элементы одного из столбцов в этих определителях равны нулю.
, т.к. все элементы одного из столбцов в этих определителях равны нулю.
Так как неизвестные находятся по формулам 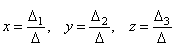 , то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.
, то в случае, когда Δ ≠ 0, система имеет единственное нулевое решение x = y = z = 0. Однако, во многих задачах интересен вопрос о том, имеет ли однородная система решения отличные от нулевого.
Теорема. Для того, чтобы система линейных однородных уравнений имела ненулевое решение, необходимо и достаточно, чтобы Δ ≠ 0.
Итак, если определитель Δ ≠ 0, то система имеет единственное решение. Если же Δ ≠ 0, то система линейных однородных уравнений имеет бесконечное множество решений.
Вопросы и упражнения для самопроверки:
1. Что такое определитель 3-го порядка?
2. Чему равен определитель третьего порядка, все элементы третьей строки которого равны нулю?
3. Что произойдет с определителем, если поменять местами какие-либо 2 столбца?
4. В каком случае определитель можно представить в виде суммы двух определителей?
5. Решить систему методом Крамера, Гаусса.
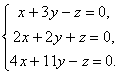
Функции и пределы.
Повторите понятия функции, области определения и области значений функции, а также §2 гл. 1 [2]. Изучите §15-19 гл. 4 [2], §4 гл. 3 и гл. 4, 5 [3]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решения примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [2] гл. 4 §15 № 4.1 - 4.3, 4.5 - 4.10, §18 № 4.35 - 4.37, 4.40 - 4.42, §19 № 4.43 - 4.44.
Из контрольной работы выполните задания с 1 по 16 своего варианта.
При вычислении пределов функций используются следующие теоремы:
1. Предел постоянной величины равен этой величине: lim с = с.
2. Предел алгебраической суммы конечного числа функций, имеющих конечные пределы, равен алгебраической сумме пределов этих функций:
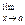 (f1 (x) ± f2 (х) ± ... ± fn (x)) =
(f1 (x) ± f2 (х) ± ... ± fn (x)) = 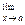 f1 (x) ±
f1 (x) ± 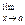 f2 (х) ± ... ±
f2 (х) ± ... ± 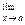 fn (x).
fn (x).
 |
3. Предел произведения конечного числа функций равен произведению пределов этих функций, если существуют конечные пределы сомножителей:
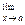 (f1 (х) ∙ f2 (х) … fn (x)) =
(f1 (х) ∙ f2 (х) … fn (x)) = 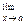 f1 (x) ∙
f1 (x) ∙ 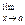 f2 (х) ...
f2 (х) ... 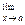 fn (x).
fn (x).
4. Предел частного двух функций равен частному пределов этих функций, если предел делителя отличен от нуля и пределы делимого и делителя существуют:
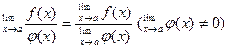
5. Постоянный множитель можно выносить за знак предела, т. е.
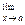 (c (∙ f (x)) = c ∙
(c (∙ f (x)) = c ∙ 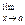 f (х), где с = const,
f (х), где с = const, 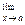 f (x) существует.
f (x) существует.
6. Если функция f(x) удовлетворяет неравенству
Ψ(x) ≤ f(x) ≤ φ(x) и если 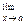 Ψ (x) = b,
Ψ (x) = b, 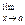 φ(x) = b , то
φ(x) = b , то 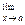 f(x) = b.
f(x) = b.
Замечание: Функция f(x) может иметь только один предел при x, стремящемся к а.
Пример 1. Найти 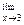 (5х2 – 6x + 7).
(5х2 – 6x + 7).
Решение: Применяя теоремы о пределах, имеем
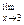 (5х2 – 6x + 7) =
(5х2 – 6x + 7) = 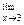 (5x2) -
(5x2) - 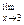 (6x) + lim 7 =
(6x) + lim 7 =
= 5 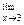 х ∙
х ∙ 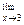 x - 6
x - 6 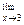 x + lim 7 = 5∙3∙3 — 6∙3 + 7 = 34.
x + lim 7 = 5∙3∙3 — 6∙3 + 7 = 34.
Пример 2. Найти 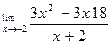
Решение: Теорему о пределе частного применить нельзя, так как при 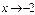 предел знаменателя равен нулю. Кроме того, и предел числителя равен нулю. Преобразуем дробь, разложив числитель на множители: 3x2 – 3x – 18 = 3 (x+2) (x-3). Поэтому
предел знаменателя равен нулю. Кроме того, и предел числителя равен нулю. Преобразуем дробь, разложив числитель на множители: 3x2 – 3x – 18 = 3 (x+2) (x-3). Поэтому
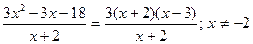 Следовательно,
Следовательно,
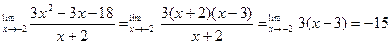
Пример 3. Найти 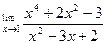
Решение: Преобразуем дробь, так как при 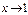 предел числителя и предел знаменателя равен нулю. Имеем.
предел числителя и предел знаменателя равен нулю. Имеем.
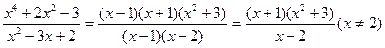
Следовательно,
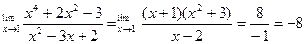
Некоторые важные пределы:
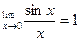
где х – длина дуги или угол в радианах;
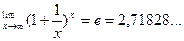
(число е – иррациональное).
При практическом нахождении пределов функций приходится иметь дело с понятиями бесконечно малой и бесконечно большой функции. Если 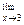 f(x) = 0, то функция f(x) называется бесконечно малой при
f(x) = 0, то функция f(x) называется бесконечно малой при 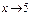 . Если
. Если 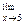 f(x) = ± ∞, то функция называется бесконечно большой при
f(x) = ± ∞, то функция называется бесконечно большой при 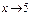 .
.
Если f(x) – бесконечно малая (бесконечно большая) при 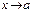 , то 1/f(x) – бесконечно большая (бесконечно малая) при
, то 1/f(x) – бесконечно большая (бесконечно малая) при 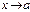 .
.
Рассмотрим некоторые особые случаи нахождения предела функции.
Пример 4. Найти 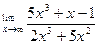
Решение: Разделив почленно числитель и знаменатель на x3 (наивысшую степень x), получим
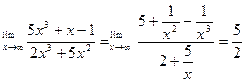
Аналогично находят предел при 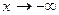
Пример 5. Вычислить 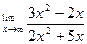
Решение: Сократим дробь на общий множитель:
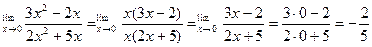
Пример 6. Найти 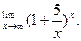
Решение. 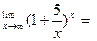
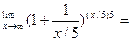
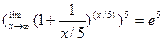
Вопросы и упражнения для самопроверки:
1. Дайте определение функции.
2. Охарактеризуйте способы задания функции.
3. Что называется областью определения функции?
4. Каков смысл предела функции в точке?
5. Перечислите теоремы о пределах, сравните с формулировками из учебника.
6. Какие замечательные пределы вы знаете?
7. Что такое числовая последовательность? Как найти предел числовой последовательности?
8. Какие функции называются бесконечно малыми и бесконечно большими?
9. Найдите:
а) 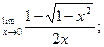 б)
б) 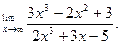
Дата: 2019-03-05, просмотров: 329.