Специальность: 19.02.10 «Технология продукции общественного питания» 1 курс
Специальность: 38.02.05 «Товароведение и экспертиза качества потребительских товаров» 1 курс

Санкт-Петербург
2016
| Одобрено предметной цикловой комиссией протокол № _____ от «_____» ____________ 20__ г. | Составлено в соответствии с государственными требованиями к минимуму содержания и уровню подготовки выпускников по специальностям: 09.02.04. |
| Председатель ______________ | Зам. директора по учебно-методической работе ___________ |
| Одобрена Методическим советом УПК протокол № _____ от «_____» ____________ 20__ г. | |
Автор: Степанова Л.Д.
Пояснительная записка
В настоящее время математика и ее методы широко применяются при решении научно-технических проблем и задач экономики. Математические методы позволяют решать проблемы планирования производства, проверять качество проектов, а также помогают при решении целого круга задач.
Математика является одной из тех наук, развитие которых служит необходимым условием ускорения научно-технического прогресса и повышения эффективности других наук.
Основной задачей дисциплины «Математика» для средних профессиональных учебных заведений состоит в том , чтобы вооружить студентов основами математических знаний, умений и навыков в объеме, необходимом для их повседневной практической деятельности, для усвоения общетехнических и специальных дисциплин, а также для дальнейшего повышения квалификации путем самообразования.
Настоящее пособие содержит варианты контрольной работы. Оно написано в соответствии с программой по математике, составленной на основании ФГОС по указанным специальностям, предназначено для студентов окончивших среднюю общеобразовательную школу и обучающихся по специальностям 100701 «Коммерция (по отраслям)»,100801 «Товароведение и экспертиза качества потребительских товаров».
Каждая тема включает 1) программу: 2) перечень параграфов из учебника; 3) методические указания к выполнению контрольной работы с решениями типовых примеров и задач; 4) вопросы и упражнения для самопроверки; 5)контрольная работа.
При подборе теоретического материала старались избежать дублирования учебника. Поэтому теоретический материал в пособии дается в сжатой форме и служит в основном для того, чтобы при решении задач можно было делать точные ссылки на нужные формулы, определения, теоремы и правила.
Общие методические указания
Данное пособие ставит своей целью оказание помощи учащимся заочного отделения в организации их работы по овладению системой знаний и умений в объеме действующей программы. При этом основной формой учебного процесса является индивидуальная самостоятельная работа, основным источником знаний учебник.
Работа с учебником. Эта работа требует не только большого напряжения, сосредоточенности и упорства, но и умения, без которого затрата сил и времени не дает должного эффекта. Следует учитывать, что нет единой системы работы над книгой, которая годилась бы во всех деталях для всех. И все же имеются некоторые общие, проверенные практикой, наиболее целесообразные условия и приемы самостоятельной работы над книгой, которые могут быть полезны и приемлемы для всех учащихся-заочников. Рассмотрим главные из них.
Планирование и систематичность занятий.
Приступая к изучению дисциплины, в первую очередь нужно ознакомиться с содержанием программы и составить план занятий, т.е. разделить материал на последовательно изучаемые темы. Эти темы можно выбрать по оглавлению учебника, пользуясь методическими указаниями или программой.
Продумав последовательность изучения дисциплины, нужно наметить сроки работы над каждой темой в соответствии с общим учебным планом.
После ознакомления с содержанием в каждой теме следует выделить основные вопросы, чтобы потом, в процессе изучения материала, найти на них ответы.
Надо приучить себя работать с книгой каждый день. Пропуски в занятиях могут войти в систему, и тогда возникает отставание в учебе.
Имея план самостоятельной работы надо ежедневно контролировать его выполнение.
Самоконтроль.
При изучении математики большое значение имеет проверка правильности понимания, усвоения и выполнения задания. Необходимо научиться самоконтролю. При этом приемы самоконтроля могут быть различные:
- проверка правильности усвоения материала путем сравнения своих формулировок с данными в учебнике (если свои записаны);
- проверка результатов решения задачи по готовому ответу, а еще лучше по готовому решению, когда сразу видно, в каких местах есть пробелы;
- по аналогичному заданию;
- прикидка верности результата;
- проверка с помощью обратных действий;
- оценка соответствия результата здравому смыслу, жизненной реальности.
О решении задач .
Решение задач является лучшим способом закрепления материала. Конечно, общих рецептов для решения разнообразных задач не существует, однако рекомендуем придерживаться
следующих советов:
1. Начинайте изучение условия задачи с тщательно выполненных наглядных рисунков, чертежей, таблиц или иллюстрированных схем, помогающих осмыслить задачу.
2. Величины, данные в условии задачи, необходимо перевести в одну систему единиц, нарушение этого правила является распространенным источником ошибок у учащихся.
3. Внимательно изучите цель, поставленную в задаче, выясните, какие теоретические положения связаны с данной задачей в целом или с некоторыми ее элементами.
4. Не следует приступать к решению задачи, не обдумав условия и не найдя плана решения.
5. Попытайтесь соотнести данную задачу с каким-либо типом задач, способ решения которых вам известен.
6. Если сразу не видно хода решения, то последовательно отвечайте на вопросы:
· что дано;
· что нужно найти;
· в чем состоит условие задачи, достаточно ли данных, чтобы найти неизвестное;
· какая связь между известными величинами?
7. Попробуйте расчленять данную задачу на серию вспомогательных, последовательное решение которых может составить решение данной задачи.
8. Найдя план решения, выполните его, убедитесь в необходимости и правильности каждого шага, произведите проверку решения и, если нужно, его исследование.
9. Подумайте, нельзя ли было решить задачу иначе; известно, что задача может иметь несколько решений, поэтому следует выделить наиболее рациональное.
10. Если решить задачу не удается, отыщите в учебной (или популярной) литературе уже решенную задачу, похожую на данную, изучите внимательно это «готовое» решение и постарайтесь извлечь из него пользу для решения данной задачи.
11. При решении задач используйте различные приемы самоконтроля, например проверку результатов по готовому ответу или готовому решению; прикидку верности результата (в задачах на вычисления); соответствие результата здравому смыслу, проверку с помощью обратных действий и др.
О контрольных работах.
Контрольные работы следует выполнять самостоятельно и лишь после того, как проработан соответствующий теоретический материал и решен необходимый минимум задач. Так как каждой теме соответствует задача или пример, то контрольную работу следует выполнять постепенно, по мере изучения материала. При решении задач следует обосновать каждый шаг решения исходя из теоретических основ курса. Не следует применять формулы, которые не входят в программу. Решение должно быть доведено до окончательного ответа.
Требования к выполнению и оформлению контрольной работы.
1. Каждая работа выполняется в отдельной тетради школьного формата. Следует пронумеровать страницы и оставить на них поля не менее 3 см для замечаний преподавателя.
2. На обложке тетради должен быть приклеен титульный лист утвержденного образца или аккуратно записаны все данные титульного листа: шифр, фамилия, имя, отчество учащегося, дисциплина и номер работы.
3. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво.
4. Решение задач желательно располагать в порядке номеров, указанных в задании, номера задач следует указывать перед условием. Решение каждой задачи следует начинать с новой страницы.
5. Условия задач должны быть обязательно переписаны полностью в контрольную тетрадь; к геометрическим задачам, кроме того, дается установленная краткая запись условия.
6. При оформлении записей в тетради необходимо выполнять общие требования к культуре их ведения. Перечислим важнейшие из этих требований:
а) учащиеся должны соблюдать абзацы, всякую новую мысль следует начинать с красной строки;
б) важные формулы, равенства, определения нужно выделять в отдельные строки, чтобы сделать их более обозримыми;
в) при описании решения задач краткая запись условия отделяется от решения, в конце решения ставится полный ответ;
г) серьезное внимание следует уделять правильному написанию сокращенных единиц, величин.
7. Решения задач должны сопровождаться краткими, но достаточно обоснованными пояснениями; используемые формулы нужно выписывать.
8. Чертежи следует выполнять карандашом с использованием чертежных инструментов, соблюдая масштаб.
9. В конце работы следует указать литературу, которой вы пользовались, проставить дату выполнения работы и подпись.
10. Если в работе допущены недочеты и ошибки, то учащийся выполняет все указания преподавателя, сделанные в рецензии. Замечания рецензента стирать нельзя.
11. Контрольные работы должны быть выполнены в срок (в соответствии с учебным планом-графиком). В период сессии работы на проверку не принимаются.
12. Работа, выполненная не по своему варианту, не учитывается и возвращается учащемуся без оценки.
13. Учащиеся, не имеющие зачета по контрольным работам курса, к экзамену не допускаются.
14. Во время экзамена зачтенные контрольные работы представляются преподавателю вместе с данными методическими указаниями.
15. Каждая контрольная работа имеет 100 вариантов. Вариант работы выбирается по двум последним цифрам шифра (номера личного дела). Например, учащиеся, имеющие шифры 23, 117, 300, 207, получат варианты 23, 17, 00, 07. Учащиеся, у которых шифры от 1 до 9, должны добавить впереди цифру 0, т. е. они получат варианты 01, 02, 03, ..., 09
Таблица вариантов.
| Вариант | |||||
Номера задач
Номера задач
Линейная алгебра
Матрицы. Основные понятия. Действия с матрицами. Определитель матриц. Свойства определителей и методы их вычислений.
Обратная матрица. Решение систем линейных уравнений в матричной форме.Метод Крамера. Метод Гаусса.
Изучите способы вычисления определителей, свойства определителей. Различные методы решения систем линейных уравнений и выполните решение примеров, используя методические указания по этой теме, внимательно разберите решения примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Выполните задание с 17-25.
Литература.
1. И.И. Валуцэ, Г.Д. Дилигул «Математика для техникумов», М.: Просвещение, 2005 г.
2. Н.В. Богомолов «Практические занятия по математике», М.: Просвещение, 2005 г.
Действия над матрицами
Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны aij = bij. Так если 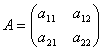 и
и 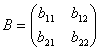 , то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
, то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если  , то
, то 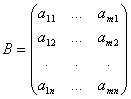 .
.
Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.
Связь между матрицей A и её транспонированной можно записать в виде 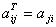 .
.
Пример 1. Найти матрицу транспонированную данной.
Решение.1
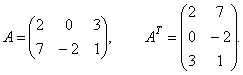
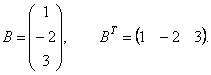
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,
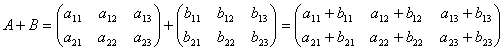
или
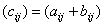
Пример 2. Найти сумму матриц:
1. 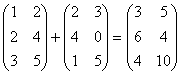 .
.
2. 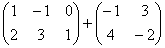 - нельзя, т.к. размеры матриц различны.
- нельзя, т.к. размеры матриц различны.
3. 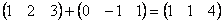 .
.
Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу 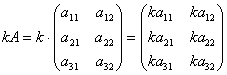 или
или 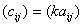 .
.
Для любых чисел a и b и матриц A и B выполняются равенства:
1. 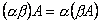
2. 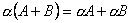
3. 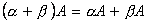 .
.
Пример 3.
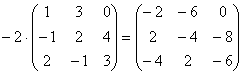 .
.
Пример 4. Найти 2A-B, если 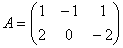 ,
, 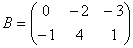 .
.
Решение.
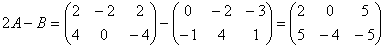 .
.
Пример 5. Найти C = –3A+4B.
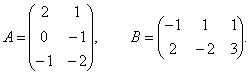
Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.
Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:
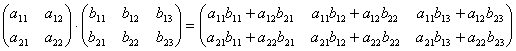 .
.
Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.
В общем случае, если мы умножаем матрицу A = (aij) размера m×n на матрицу B = (bij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.
Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,
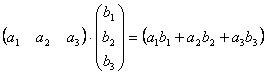 .
.
Пример 6.
Решение. Пусть 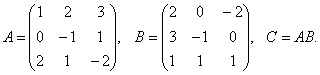
Найти элементы c12, c23 и c21 матрицы C.
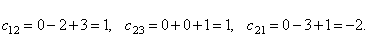
Пример 7. Найти произведение матриц.
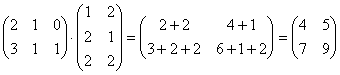 .
.
1.  .
.
2. 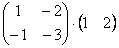 - нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
- нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
3. Пусть 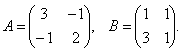
Найти АВ и ВА.
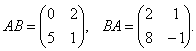
4. 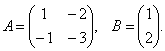
Найти АВ и ВА.
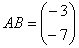 , B·A – не имеет смысла.
, B·A – не имеет смысла.
Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.
Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.
Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если 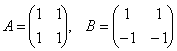 , то
, то
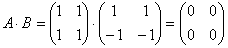 .
.
Определители
Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов 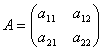 .
.
Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a11a22 – a12a21.
Определитель обозначается символом 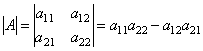 .
.
Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.
Пример 8. Вычислить определители второго порядка.
1. 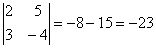
2. 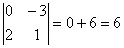 .
.
3. Вычислить определитель матрицы D, если D= -А+2В и
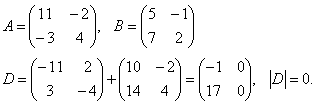
Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:
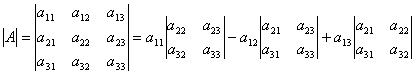 .
.
Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a11, a12, a13 и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.
Пример 9. Вычислить определитель третьего порядка.
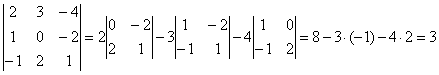
.
Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки "+" и "–" у слагаемых чередуются.
Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.
Свойства определителей
1. Если квадратная матрица AT является транспонированной матрицей A, то их определители совпадают |AT | = |A|, т.е. определитель не меняется, если заменить его строки столбцами и обратно, например, для определителя третьего порядка 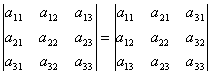 .
.
2. При перестановке 2-х строк или столбцов определитель изменит знак на противоположный, сохраняя абсолютную величину, т.е., например,
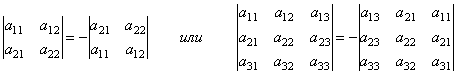
3. Если определитель имеет две одинаковые строки или столбца, то он равен нулю. 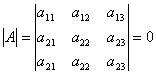 .
.
4. Общий множитель строки или столбца можно выносить за знак определителя. 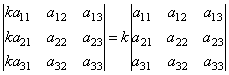 .
.
5. Если все элементы какой–либо строки или столбца определителя равны нулю, то сам определитель равен нулю.
6. Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель можно представить в виде суммы 2-х определителей по формуле, например,
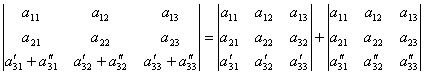 .
.
7. Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины.
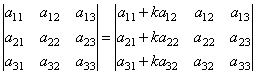 .
.
Эти свойства определителей довольно часто используются при вычислении определителей и в различных задачах.
Пример13.
1. Найти матрицу, обратную данной 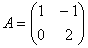 . Сделать проверку.
. Сделать проверку.
|A| = 2. Найдем алгебраические дополнения элементов матрицы A.
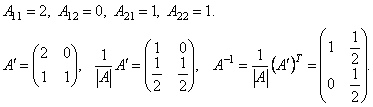
Проверка:
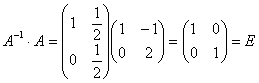 .
.
Аналогично A∙A-1 = E.
2. Найти элементы 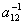 и
и 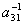 матрицы A-1 обратной данной
матрицы A-1 обратной данной
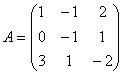 .
.
Вычислим |A| = 4. Тогда 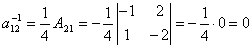 .
.
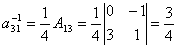 .
.
3. 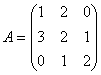 . Найдем обратную матрицу.
. Найдем обратную матрицу.
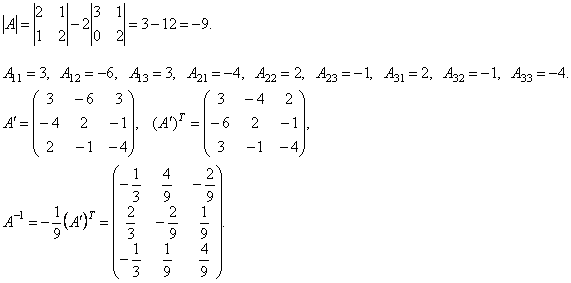
Системы линейных уравнений
Системой m линейных уравнений с n неизвестными называется система вида
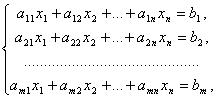
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 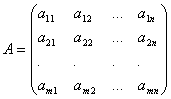 , которую назовём матрицей системы.
, которую назовём матрицей системы.
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
1. Система может иметь единственное решение.
2. Система может иметь бесконечное множество решений. Например, 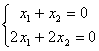 . Решением этой системы является любая пара чисел, отличающихся знаком.
. Решением этой системы является любая пара чисел, отличающихся знаком.
3. И третий случай, когда система вообще не имеет решения. Например, 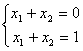 , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Рассмотрим способы нахождения решений системы.
Метод Крамера
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
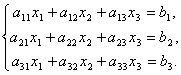
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
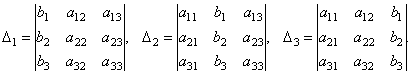
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
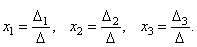
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Пример . Решить систему уравнений
1. 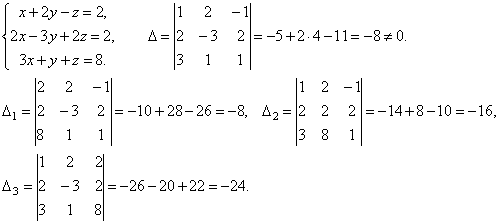
Итак, х=1, у=2, z=3.
Метод Гаусса
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
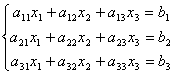 .
.
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:

Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на 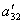 , умножим на
, умножим на 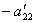 и сложим со вторым. Тогда будем иметь систему уравнений:
и сложим со вторым. Тогда будем иметь систему уравнений:
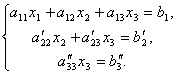
Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
1. перестановка строк или столбцов;
2. умножение строки на число, отличное от нуля;
3. прибавление к одной строке другие строки.
Пример: Решить системы уравнений методом Гаусса.
1. 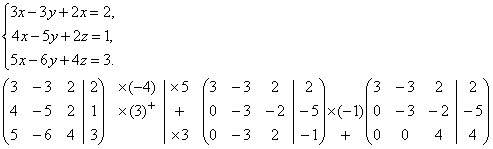
Вернувшись к системе уравнений, будем иметь
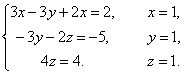
2. 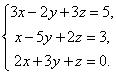
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
3. 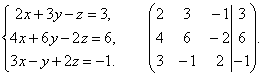
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
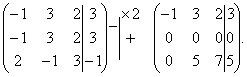
Вернемся к системе уравнений. 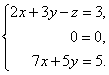
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
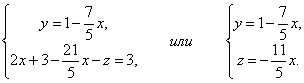
Таким образом, система имеет бесконечное множество решений.
Функции и пределы.
Повторите понятия функции, области определения и области значений функции, а также §2 гл. 1 [2]. Изучите §15-19 гл. 4 [2], §4 гл. 3 и гл. 4, 5 [3]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решения примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [2] гл. 4 §15 № 4.1 - 4.3, 4.5 - 4.10, §18 № 4.35 - 4.37, 4.40 - 4.42, §19 № 4.43 - 4.44.
Из контрольной работы выполните задания с 1 по 16 своего варианта.
При вычислении пределов функций используются следующие теоремы:
1. Предел постоянной величины равен этой величине: lim с = с.
2. Предел алгебраической суммы конечного числа функций, имеющих конечные пределы, равен алгебраической сумме пределов этих функций:
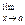 (f1 (x) ± f2 (х) ± ... ± fn (x)) =
(f1 (x) ± f2 (х) ± ... ± fn (x)) = 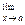 f1 (x) ±
f1 (x) ± 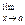 f2 (х) ± ... ±
f2 (х) ± ... ± 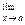 fn (x).
fn (x).
 |
3. Предел произведения конечного числа функций равен произведению пределов этих функций, если существуют конечные пределы сомножителей:
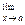 (f1 (х) ∙ f2 (х) … fn (x)) =
(f1 (х) ∙ f2 (х) … fn (x)) = 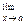 f1 (x) ∙
f1 (x) ∙ 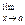 f2 (х) ...
f2 (х) ... 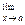 fn (x).
fn (x).
4. Предел частного двух функций равен частному пределов этих функций, если предел делителя отличен от нуля и пределы делимого и делителя существуют:
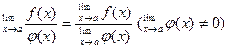
5. Постоянный множитель можно выносить за знак предела, т. е.
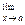 (c (∙ f (x)) = c ∙
(c (∙ f (x)) = c ∙ 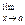 f (х), где с = const,
f (х), где с = const, 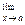 f (x) существует.
f (x) существует.
6. Если функция f(x) удовлетворяет неравенству
Ψ(x) ≤ f(x) ≤ φ(x) и если 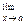 Ψ (x) = b,
Ψ (x) = b, 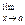 φ(x) = b , то
φ(x) = b , то 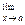 f(x) = b.
f(x) = b.
Замечание: Функция f(x) может иметь только один предел при x, стремящемся к а.
Пример 1. Найти 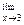 (5х2 – 6x + 7).
(5х2 – 6x + 7).
Решение: Применяя теоремы о пределах, имеем
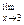 (5х2 – 6x + 7) =
(5х2 – 6x + 7) = 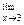 (5x2) -
(5x2) - 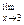 (6x) + lim 7 =
(6x) + lim 7 =
= 5 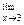 х ∙
х ∙ 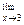 x - 6
x - 6 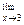 x + lim 7 = 5∙3∙3 — 6∙3 + 7 = 34.
x + lim 7 = 5∙3∙3 — 6∙3 + 7 = 34.
Пример 2. Найти 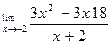
Решение: Теорему о пределе частного применить нельзя, так как при 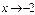 предел знаменателя равен нулю. Кроме того, и предел числителя равен нулю. Преобразуем дробь, разложив числитель на множители: 3x2 – 3x – 18 = 3 (x+2) (x-3). Поэтому
предел знаменателя равен нулю. Кроме того, и предел числителя равен нулю. Преобразуем дробь, разложив числитель на множители: 3x2 – 3x – 18 = 3 (x+2) (x-3). Поэтому
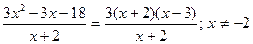 Следовательно,
Следовательно,
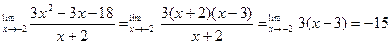
Пример 3. Найти 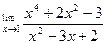
Решение: Преобразуем дробь, так как при 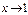 предел числителя и предел знаменателя равен нулю. Имеем.
предел числителя и предел знаменателя равен нулю. Имеем.
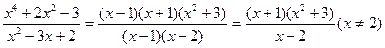
Следовательно,
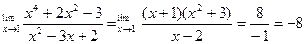
Некоторые важные пределы:
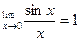
где х – длина дуги или угол в радианах;
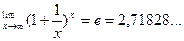
(число е – иррациональное).
При практическом нахождении пределов функций приходится иметь дело с понятиями бесконечно малой и бесконечно большой функции. Если 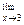 f(x) = 0, то функция f(x) называется бесконечно малой при
f(x) = 0, то функция f(x) называется бесконечно малой при 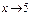 . Если
. Если 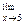 f(x) = ± ∞, то функция называется бесконечно большой при
f(x) = ± ∞, то функция называется бесконечно большой при 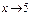 .
.
Если f(x) – бесконечно малая (бесконечно большая) при 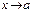 , то 1/f(x) – бесконечно большая (бесконечно малая) при
, то 1/f(x) – бесконечно большая (бесконечно малая) при 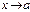 .
.
Рассмотрим некоторые особые случаи нахождения предела функции.
Пример 4. Найти 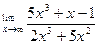
Решение: Разделив почленно числитель и знаменатель на x3 (наивысшую степень x), получим
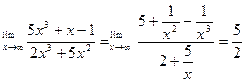
Аналогично находят предел при 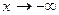
Пример 5. Вычислить 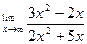
Решение: Сократим дробь на общий множитель:
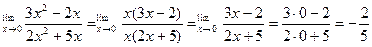
Пример 6. Найти 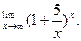
Решение. 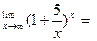
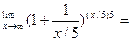
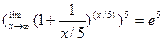
Вопросы и упражнения для самопроверки:
1. Дайте определение функции.
2. Охарактеризуйте способы задания функции.
3. Что называется областью определения функции?
4. Каков смысл предела функции в точке?
5. Перечислите теоремы о пределах, сравните с формулировками из учебника.
6. Какие замечательные пределы вы знаете?
7. Что такое числовая последовательность? Как найти предел числовой последовательности?
8. Какие функции называются бесконечно малыми и бесконечно большими?
9. Найдите:
а) 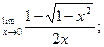 б)
б) 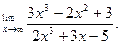
Таблица формул дифференцирования.
| 1. | c’ = 0 | 12. | (ln u)’ = 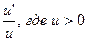
|
| 2. | x’ = 1 | 13. | (logau)’ = 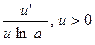
|
| 3. | (u ± v)’ = u’ ± v’ | 14. | (sin u)’ = cos u ∙ u’ |
| 4. | (uv)’ = uv’ + vu’ | 15. | (cos u)’ = - sin u ∙ u’ |
| 5. | (cu)’ = cu | 16. | (tg u)’ = 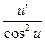 = sec2 u ∙ u’ = sec2 u ∙ u’
|
| 6. | 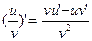
| 17. | (ctg u)’ = - 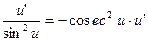
|
| 7. | 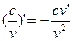
| 18. | (arcsin u)’ = 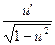
|
| 8. | (un)’ = nun-1 u’ | 19. | (arccos u)’ = - 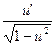
|
| 9. | 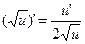
| 20. | (arctg u)’ = 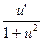
|
| 10. | (au)’ = au ln a ∙ u’ | 21. | (arcctg u)’ = - 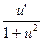
|
| 11. | (eu)’ = eu ln eu’ = euu’ |
Здесь u и v – дифференцируемые функции от x, а с – постоянная величина.
Пример 1 . Найти производную функции f(x) = 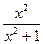
Решение. Дифференцируем функцию по формулам 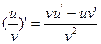 (un) = nun-1u’:
(un) = nun-1u’:
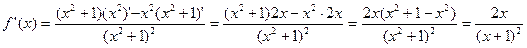
Пример 2. Найти производную функции y = sin3φ и вычислить ее значение при φ = π/3.
Решение. Это сложная функция с промежуточным аргументом sinφ. Дифференцируем ее по формулам (un)’ = nun-1 u’ , (sin u)’ = cos u ∙ u’:
f’(φ) = 3sin2φ (sinφ)’ = 3sin2φ cosφ
Вычислим значение производной при φ = π/3:
f’ (π/3) = 3 sin2 (π/3) cos (π/3) = 3 ( 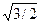 )2∙ (1/2) = 3 ∙ (3/4) ∙ (1/2) = 9/8
)2∙ (1/2) = 3 ∙ (3/4) ∙ (1/2) = 9/8
Пример 3. Найти производную функции f(x) = ln 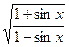
Решение. Сначала преобразуем функцию, используя свойства логарифмов:
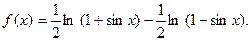
Дифференцируя, получим:
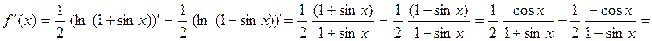
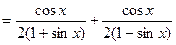

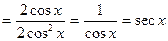
Приложение производной к исследованию функций.
Дифференцируемая функция y = f ( x ) возрастает на промежутке ] a, b [, если ее производная положительна в каждой точке этого промежутка.
Дифференцируемая функция y = f ( x ) убывает на промежутке ] a, b [, если ее производная отрицательна в каждой точке этого промежутка.
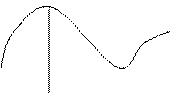
Функция y = f ( x ) имеет максимум в точке x = x 1 (рис. 1), если для всех значений х, достаточно близких к х1, выполняется неравенство f (х) < f (х1); x = x 1 - точка максимума; ymax = f (х1) - максимум функции.
Функция y = f ( x ) имеет минимум в точке х = x 2 (рис. 1), если для всех значений х, достаточно близких к x 2 , выполняется неравенство f ( x ) > f (х2); х = x 2 - точка минимума; ymin = f ( x 2 ) - минимум функции.
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - экстремальными.
Точки, в которых производная функции обращается в нуль, называются критическими точками I рода.
y 
 |
y = f(x)
f(x1)
 f(x2)
f(x2)
0  x1 x2 x
x1 x2 x
рис. 1
Первое достаточное условие существования экстремума функции. Если при переходе через критическую точку I рода х = х0 производная функции у = f (х) меняет знак, то х = х0 - точка экстремума.
При этом если производная меняет знак с плюса на минус, то х = х0 - точка максимума, a ymax = f ( x 0 ). Если же производная меняет знак с минуса на плюс, то х = х0 - точка минимума, a ymin = f ( x 0 ).
Второе достаточное условие существования экстремума функции. Если в точке х = х0 первая производная функции у = f (х) обращается в нуль, а вторая производная отлична от нуля, то х = х0 - точка экстремума.
При этом если вторая производная в этой точке положительна (f’’(x0) > 0), то х = х0 - точка минимума; если вторая производная в этой точке отрицательна ( f "( x 0 ) < 0), то х = х0 - точка максимума.
Направление вогнутости и точки перегиба кривой. Говорят, что на промежутке ] а, b [ кривая обращена выпуклостью вверх или выпукла ( 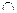 ), если она лежит ниже касательной, проведенной в любой ее точке (рис. 2).
), если она лежит ниже касательной, проведенной в любой ее точке (рис. 2).
y Говорят, что кривая на промежутке ] b, с [ обращена
 выпуклая выпуклостью вниз или вогнута (
выпуклая выпуклостью вниз или вогнута (  ), если она лежит выше
), если она лежит выше

 y = f ( x ) касательной, проведенной в любой ее точке (рис. 2).
y = f ( x ) касательной, проведенной в любой ее точке (рис. 2).
Точка А, в которой меняется направление вогнутости кривой,
А называется точкой перегиба кривой (рис. 2).
График дифференцируемой функции у = f(x) является
 выпуклым на промежутке ] а; b [ если вторая производная
выпуклым на промежутке ] а; b [ если вторая производная
вогнутая функции отрицательна в каждой точке этого промежутка.
 a b c x График дифференцируемой функции у = f ( x ) является
a b c x График дифференцируемой функции у = f ( x ) является
рис. 2 вогнутым на промежутке ] b; с [, если вторая производная функции положительна в каждой точке этого промежутка.
Точки, в которых вторая производная функции обращается в нуль, называются критическими точками II рода.
Если при переходе через критическую точку II рода х = x0 вторая производная функция меняет знак, то х = х0 - абсцисса точки перегиба. Ордината точки перегиба равна значению функции в точке х0, т. е. ут п = f(x0); А(х0; f ( x 0 )) - точка перегиба графика функции у = f (х).
Исследование функций и построение их графиков. Исследование функции можно проводить по следующей схеме:
1. Найти область определения функции.
2. Найти точки пересечения графика функции с осями координат.
3. Найти промежутки монотонности и экстремумы функции.
4. Найти направление вогнутости и точки перегиба графика функции.
5. Для уточнения графика функции рекомендуется найти несколько дополнительных точек из уравнения функции.
Пример. Построить график функции у = х3 - 6x2 + 9x - 3.
1. Функция определена на всей числовой прямой, т. е. D(y) = R.
2. Данная функция не является ни четной, ни нечетной; кроме того, она не является периодической.
3. Найдем точку пересечения графика с осью Оу: полагая х = 0, получим y = -3. Точки пересечения графика с осью Ох в данном случае найти затруднительно.
4. Очевидно, что график функции не имеет асимптот.
5.  Найдем производную: у' = 3х2 - 12х + 9. Далее, имеем (Зх2 - 12х + 9 = 0) <=> (х2 - 4х + 3 = 0) <=>
Найдем производную: у' = 3х2 - 12х + 9. Далее, имеем (Зх2 - 12х + 9 = 0) <=> (х2 - 4х + 3 = 0) <=> 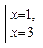 Точки х=1 и х = 3 делят область определения функции на три промежутка: - ∞ ,1 [,
Точки х=1 и х = 3 делят область определения функции на три промежутка: - ∞ ,1 [,

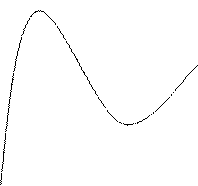 y (1;1) ] 1,3 [ и ] 3, + ∞ [ В промежутках ] - ∞, 1 [и] 3, + ∞ [ у' > 0, т е.
y (1;1) ] 1,3 [ и ] 3, + ∞ [ В промежутках ] - ∞, 1 [и] 3, + ∞ [ у' > 0, т е.
функция возрастает, а в промежутке ] 1, 3 [ y '< 0 т. е. функция
 убывает.
убывает.
0 x При переходе через точку х = 1 производная меняет знак с
плюса на минус, а при переходе через точку х = 3 - с минуса на
(2;1) плюс. Значит, ymax = y(1) =1, ymin = y(3) = -3
6. Найдем вторую производную: у" = 6х - 12; 6 x - 12 = 0, x =
(0;-3) (3;-3) = 2. Точка х = 2 делит область определения функции на два
промежутка ] - ∞, 2[ и ]2, + ∞[. В первом из них у" < 0, а во
втором у" > 0, т. е. в промежутке ] - ∞, 2[ кривая выпукла
рис. 3 вверх, а в промежутке ]2, + ∞[ выпукла вниз.
Таким образом, получаем точку перегиба (2; -1).
7. Используя полученные данные, строим искомый график (рис. 3).
Интегральное исчисление
Неопределенный интеграл и его свойства. Непосредственное интегрирование. Определенный интеграл. Вычисление и свойства определенного интеграла. Применение определенного интеграла.
По данной теме сначала изучите §7-10 (1, 2), 11 (1, 2) гл. 3, §12, 14 (1 - 3) гл. 4 [3] или § 1 - 14 гл. 8 [4]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Запишите таблицу интегралов. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [3] гл. 3 §10 №3.5-3.8, 3.12, гл. 4 §12 № 4.1, §14 №4.3 - 4.29 или [4], гл. 8 №1-5, 8-13, 17-21, 23-27, 42-49, 50-55, 60-63.
Из контрольной работы выполните задания с 51 по 75 своего варианта.
Литература.
1. «Алгебра и начало анализа», под ред. Г.Н. Яковлева, М.: 1981 г. ч. I.
2. «Алгебра и начало анализа», под ред. Г.Н. Яковлева, М.: 1981 г. ч. II.
3. И.И. Валуцэ, Г.Д. Дилигул «Математика для техникумов», М.: Просвещение, 2005 г.
4. Н.В. Богомолов «Практические занятия по математике», М.: Просвещение, 2005 г.
Неопределенный интеграл.
Понятие неопределенного интеграла. Дифференцирование - это действие, с помощью которого по данной функции находится ее производная или дифференциал. Например, если F(x ) = x 10 , то F ' (х) = 10х9, dF (х) = 10х9 d х.
Интегрирование - это действие, обратное дифференцированию. С помощью интегрирования по данной производной или дифференциалу функции находится сама функция. Например, если F ' х = 7 x 6 , то F (х) = х7 , так как (х7)’ = 7х6 .
Дифференцируемая функция F ( x ), x 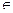 ]a b[ называется первообразной для функции f (х) на интервале ]a; b[, если F '( x ) = f ( x ) для каждого х
]a b[ называется первообразной для функции f (х) на интервале ]a; b[, если F '( x ) = f ( x ) для каждого х 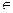 ] а; b [.
] а; b [.
Так, для функции f { x ) = 1/cos2 х первообразной служит функция F (х) = tg х, поскольку (tg x)'= = 1/cos2 x.
Совокупность всех первообразных функций f ( x ) на интервале ]а; b[ называют неопределенным интегралом от функции f ( x ) на этом интервале и пишут 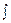 f ( x ) dx = F ( x ) + С. Здесь f ( x ) dx -подынтегральное выражение; f ( x )- подынтегральная функция; х - переменная интегрирования; С - произвольная постоянная.
f ( x ) dx = F ( x ) + С. Здесь f ( x ) dx -подынтегральное выражение; f ( x )- подынтегральная функция; х - переменная интегрирования; С - произвольная постоянная.
Например, 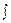 5x ’ dx = х5 + С, так как (x5 + С)' = 5х1.
5x ’ dx = х5 + С, так как (x5 + С)' = 5х1.
Приведем основные свойства неопределенного интеграла.
1. Дифференциал неопределенного интеграла равен подынтегральному выражению:
d 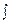 f ( x ) dx = f ( x ) dx .
f ( x ) dx = f ( x ) dx .
2. Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной, т. е.
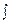 dF ( x ) = F ( x + C .
dF ( x ) = F ( x + C .
3. Постоянный множитель можно выносить за знак неопределенного интеграла:
∫ af(x) dx = a ∫ f(x)dx.
4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от каждой функции:
∫ ( f 1 (х) ± f 2 (x)) dx = ∫ f 1 (х) dx ± ∫ f 2 ( x ) dx .
Определенный интеграл.
По данной теме сначала изучите §7-10 (1, 2), 11 (1, 2) гл. 3, §12, 14 (1 - 3) гл. 4 [3] или § 1 - 14 гл. 8 [4]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Решите следующие задачи: [3] гл. 3 §10 №3.5-3.8, 3.12, гл. 4 §12 № 4.1, §14 №4.3 - 4.29 или [4], гл. 8 №1-5, 8-13, 17-21, 23-27, 42-49, 50-55, 60-63.
Из контрольной работы выполните задание с 76 по 88 своего варианта.
Понятие определенного интеграла. Непосредственное вычисление определенного интеграла производится по формуле Ньютона—Лейбница;
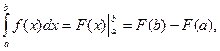
где a - нижний предел, b - верхний предел, F ( x ) - какая-нибудь первообразная функции f ( x ).
Из этой формулы виден порядок вычисления определенного интеграла:
1) Находят одну из первообразных F ( x ) данной функции;
2) Находят значения F ( x ) при x = a и x = b;
3) Вычисляют разность F ( b ) – F ( a ).
Пример 1. Вычислить интеграл 
Решение. Воспользуемся определением степени с дробным и отрицательным показателем и вычислим определенный интеграл:
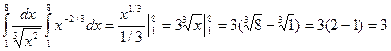
Приведем основные свойства определенного интеграла.
1. Перестановка пределов интеграла знак интеграла меняется на противоположный:
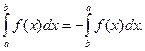
2. Отрезок интегрирования можно разбивать на части:
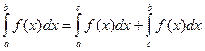
3. Постоянный множитель можно выносить за знак интеграла:
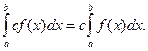
4. Интеграл от суммы функций равен сумме интегралов от всех слагаемых:
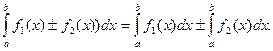
Пример 2. Вычислить интеграл 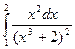
Решение.
1) Произведем подстановку x3 + 2 = t; тогда 3x3dx = dt, x2dx = 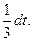
2) Определим пределы интегрирования для переменной t. При x = 1 получаем tн = 13+2 = 3, при x = 2 получаем tв = 23 + 2 = 10.
3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим:
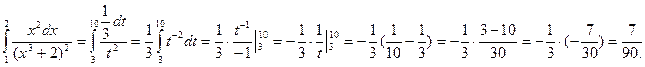
Пример 3. Вычислить интеграл 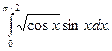
Решение.
1) Положим cos x = t ; тогда - sin xdx = dt и sin xdx = - dt ;
2) Определим пределы интегрирования для переменной t : tH = cos 0 = tH = cos (π/2) = 0.
3) Выразив подынтегральное выражение через t и dt и перейдя к новым пределам, получим:
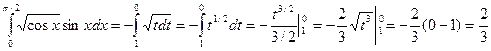
Вопросы и упражнения для самопроверки:
1. Дайте определение определенного интеграла.
2. Перечислите основные свойства определенного интеграла.
3. В чем заключается геометрический смысл определенного интеграла?
Комплексные числа
Поданной теме сначала изучите § 1—9 гл: 9 [3]. Затем ознакомьтесь с методическими указаниями по этой теме и внимательно разберите решение примеров из данного пособия. Ответьте на вопросы и выполните упражнения для самопроверки. Самостоятельно закончите решение некоторых примеров. Из контрольной работы выполните задание с 89 по 96 своего варианта.
Основные понятия и определения. Решение многих задач сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов математики. Стремление сделать уравнения разрешимыми - одна из главных причин расширения понятия числа.
Так, для разрешимости уравнения х + а = b положительных чисел недостаточно и приходится вводить отрицательные числа и нуль.
Для решения уравнения ах =b (а≠О) недостаточно целых чисел и приходится вводить дробные числа. Целые и дробные числа образуют множество Q рациональных чисел.
На множестве рациональных чисел разрешимы уравнения вида ах =b (а≠О), однако уравнение х2=2 не имеет рациональных корней. Необходимость решения таких уравнений явилась одной из причин введения иррациональных чисел.
Рациональные и иррациональные числа образуют множество R действительных чисел.
Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, уравнение x2+1=0 не имеет действительных корней. Поэтому приходится расширять множество действительных чисел до нового множества; такого, чтобы в этом множестве уравнения вида x2 +a2 =0 имели решения.
Корень уравнения x2+1=0 или x2-1=0 называется мнимой единицей и обозначается буквой ί
Таким образом, символ ί удовлетворяет условию ί2= -1.
Комплексным числом называется выражение вида α+bί , где а и b— действительные числа, а ί—мнимая единица.
Число а называется действительной частью комплексного числа, а число bί — мнимой частью.
Комплексное число часто обозначают одной буквой z. Множество комплексных чисел принято обозначать буквой С.
Запись комплексного числа в виде z =a +bί называется алгебраической формой записи комплексного числа. Два комплексных числа a1+ b1ί и a2+b2 ί называются равными тогда и только тогда, когда а1 = а2 и b1=b2, т. е. когда равны их действительные части и коэффициенты при мнимой части.
Понятия «больше» и «меньше» для комплексных чисел не определяются.
Комплексное число z = 0+ называется нулем и обозначается .0; комплексное число z=a+Qί отождествляется с действительным числом . а, т. е. комплексное число z = 0 +bί называется чисто мнимым и обозначается bί, т, е. 0+bί = bί
Число ί является единственным числом, которое одновременно и действительное, и чисто мнимое.
Комплексные числа a+bί и a- bί называются сопряженными.
Действия над комплексными числами в алгебраической форме.
Суммой двух комплексных чисел z 1= a + bί и z2= c +dί. называется комплексное число
z1 +z2= (a + c) + (b + d)ί.
Умножение двух комплексных чисел выполняется по правилу:
(a + bί)(c + dί) = (aс + bd) + (ad + db)ί.
Вычитание комплексных чисел вводится как операция, обратная сложению; деление комплексных чисел вводится как операция, обратная умножению.
Правила вычитания и деления комплексных чисел z1= a + bί и z2 = c +dί определяется формулами
z2-z1= (a + bί) – (c + dί) = (a – c) + (b – d)ί.
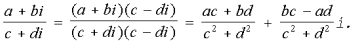
Формула теряет смысл, если c + dί = 0, так как тогда c2 + d2 = 0, т. е. деление на нуль и во множестве комплексных чисел исключается.
Формулы, определяющие правила действий над комплексными числами в алгебраической форме, не нуждаются в запоминании.
Формулы суммы, разности и произведения комплексных чисел получаются автоматически, если формально выполнить соответствующие действия над двучленами a + bί и c +dί и заменить ί2 на —1.
Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю.
Возведение комплексного числа в степень производится по формулам возведения двучлена в степень, но при этом надо, учитывать, что:
ί 1 = ί ί4 n +1 = ί1= ί
ί2 = -1 ί4n+2= ί2 = -1
ί3 = -ί ί4n+3= ί3 = - ί
ί4 = 1 ί4n = 1.
Пример 1. Найти сумму комплексных чисел z1=(2 + 3ί) и z2= (5 + ί) :
Сумму находим формальным сложением двучленов
(2 + 3ί) + (5 + ί) = (2 + 5) + (3 + 1)ί = 7 + 4ί;
Пример 2.Найти разность комплексных чисел z1=5 – 8ί и z2= 2 + 3ί :
Разность находим формальным вычитанием двучленов (5 – 8ί) – (2 + 3ί) = (3 – 2) + (– 8 – 3)ί = 1–11ί;
Пример 3.Найти произведение комплексных чисел z1= -1 + 3ί и z2= 2 + 5ί :
Произведение находим формальным перемножением двучленов (– 1 + 3ί)(2 + 5ί) = – 2 – 5ί + 6ί + 15ί2 = – 2 – 5ί + 6ί – 15 = – 17 + ί;
Пример 4. Найти произведение комплексных чисел z1= 2 + 3ί и z2= 2 - 3ί :
(2 + 3ί)(2 – 3ί) = 4 – 6ί + 6ί – 9ί2 = 4 + 9 = 13.
Из четвертого примера следует, что результатом сложения, вычитания, произведения двух комплексных чисел может быть число действительное. В частности, при умножении двух сопряженных комплексных чисел a + bί и a – bί, в результате получается действительное число, равное сумме квадратов действительной части и коэффициента при мнимой части. Произведение двух чисто мнимых чисел – действительное число. Например: 5ί•3ί= 15ί2 = – 15; – 2ί•3ί= – 6ί2 = 6.
Обычно деление комплексных чисел выполняют путем умножения делимого и делителя на число, сопряженное делителю.
Например,
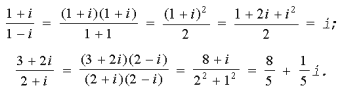
Опираясь на введенные определения нетрудно проверить, что для комплексных чисел справедливы коммутативный, ассоциативный и дистрибудивный законы. Кроме того, применение операций сложения, умножения, вычитания и деления к двум комплексным числам снова приводит к комплексным числам.Приведем классификацию комплексных чисел:
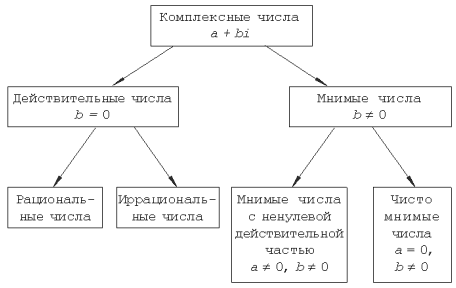
Геометрическая  интерпретация комплексных чисел
интерпретация комплексных чисел
Известно, что отрицательные числа были введены в связи с решением линейных уравнений с одной переменной. В конкретных задачах отрицательный ответ истолковывался как значение направленной величины (положительные и отрицательные температуры, передвижения в противоположных направлениях, прибыль и долг и т.п.). Однако еще в ХVI веке многие математики не признавали отрицательных чисел. Только с введением координатной прямой и координатной плоскости отчетливо проявился смысл отрицательных чисел, и они стали такими же «равноправными» и понятными, как и натуральные числа. Аналогично обстоит дело с комплексными числами. Смысл их отчетливо проявляется при введении их геометрической интерпретации.
Геометрическая интерпретация комплексных чисел состоит в том, что каждому комплексному числу z = x + yi ставится в соответствие точка (x, y) координатной плоскости таким образом, что действительная часть комплексного числа представляет собой  абсциссу, а коэффициент при мнимой части – ординату точки.
абсциссу, а коэффициент при мнимой части – ординату точки.
Таким образом, устанавливается взаимно однозначное соответствие между множеством комплексных чисел и множеством точек координатной плоскости. Подобным образом было установлено соответствие между множеством действительных чисел и множеством точек числовой прямой.
На рисунке 1 изображена координатная плоскость. Числу 2 + 3i соответствует точка A(2, 3) плоскости; числу 2 – 3i – точка B(2, – 3); числу – 2 + 3i – точка C(– 2, 3); числу – 2 – 3i – точка D(– 2; – 3). Числу 3i соответствует точка E(0, 3); а числу – 3i – точка F(0, – 3). Итак, каждому комплексному числу соответствует единственная точка координатной плоскости и, обратно, каждой точке координатной плоскости соответствует единственное комплексное число, при этом двум различным комплексным числам соответствуют две различные точки координатной плоскости. Ясно, что действительным числам x + 0i соответствуют точки оси абсцисс, а чисто мнимым числам 0 + yi точки оси ординат. Поэтому ось Oy называют мнимой, а ось Ox – действительной. Сопряженным комплексным числам 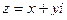 и
и 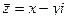 соответствуют точки, симметричные относительно оси абсцисс (рис. 2).
соответствуют точки, симметричные относительно оси абсцисс (рис. 2).
Тригонометрическая форма комплексного числа
 Точка координатной плоскости, соответствующая комплексному числу z = x + yί, может быть указана по-другому: ее координатами могут быть расстояние r от начала координат и величина угла φ между положительной полуосью Ox и лучом Oz (рис. 3).
Точка координатной плоскости, соответствующая комплексному числу z = x + yί, может быть указана по-другому: ее координатами могут быть расстояние r от начала координат и величина угла φ между положительной полуосью Ox и лучом Oz (рис. 3).
Расстояние r от начала системы координат до точки, соответствующей комплексному числу z, называют модулем этого числа. На основании теоремы Пифагора (рис. 2) получается формула: 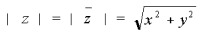
Если комплексное число z изображается точкой оси абсцисс (т.е. является действительным числом), то его модуль совпадает с абсолютным значением. Все комплексные числа, имеющие модуль 1, изображаются точками единичной окружности – окружности с центром в начале системы координат, радиуса 1 (рис. 4).
 Аргументом комплексного числа z≠ 0 называется величина угла φ между положительным направлением действительной оси и вектором, соответствующим этому числу(рис. 3).
Аргументом комплексного числа z≠ 0 называется величина угла φ между положительным направлением действительной оси и вектором, соответствующим этому числу(рис. 3).
Сопряженные комплексные числа 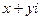 и
и 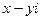 имеют один и тот же модуль
имеют один и тот же модуль 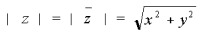 и аргументы, отличающиеся знаком: j = – j.
и аргументы, отличающиеся знаком: j = – j.
В отличие от модуля аргумент комплексного числа определяется неоднозначно. Аргумент одного и того же комплексного числа может иметь бесконечно много значений, отличающихся друг от друга на число, кратное 360°. Например, число z (рис. 3) имеет модуль r, аргумент же этого числа может принимать значения ; j + 360°; j + 720°; j + 1080°; … или значения j – 360°; j –720°; j – 1080°; … Данное значение модуля r и любое из приведенных выше значений аргумента определяют одну и ту же точку плоскости, соответствующую числу z.Пусть точке с координатами (x; y) соответствует комплексное число z = x + yi. Запишем это комплексное число через его модуль и аргумент. Воспользуемся определением тригонометрических функций синуса и косинуса (рис. 3):
x = r cos j; y = r sin j.
Тогда число z выражается через модуль и аргумент следующим образом:
z = x + yί = r(cos j + ί sin j).
Выражение z = r(cos j + ίsin j) называют тригонометрической формой комплексного числа, в отличии от выражения z = x + yi, называемого алгебраической формой комплексного числа.
Приведем примеры обращения комплексных чисел из алгебраической формы в тригонометрическую:
Для числа i имеем r = 1, j = 90°, поэтому ί = 1(cos 90° + ί sin 90°);
Для числа – 1 имеем r = 1, j = 180°, поэтому – 1 = 1(cos 180° + ί sin 180°);
Для числа 1 + ί имеем 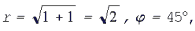 поэтому
поэтому 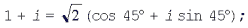
Для числа 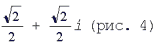 имеем r = 1, j = 45°, поэтому
имеем r = 1, j = 45°, поэтому 
Для числа 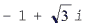 имеем r = 2, j = 120°, поэтому
имеем r = 2, j = 120°, поэтому 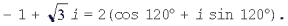
Справедливость приведенных равенств нетрудно проверить путем подстановки в их правой части числовых значений тригонометрических функций. Итак, для того, чтобы комплексное число, заданное в алгебраической форме, обратить в тригонометрическую форму, необходимо найти его модуль r и аргумент j, пользуясь формулами:
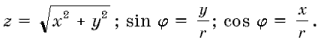
Пример 5. Представить в тригонометрической форме число 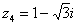
Найдем его модуль и аргумент.
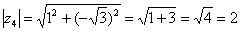
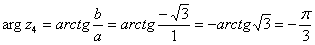
Таким образом:
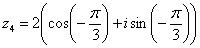 – число
– число 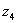 в тригонометрической форме.
в тригонометрической форме.
Арифметические действия над комплексными числами, заданными в тригонометрической форме, производятся следующим образом. Пусть z 1 = r 1 (cos φ 1 + i sin φ 1 ) и z 2 = r 2 (cos φ 2 + i sin φ 2 ). Имеем:
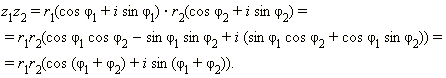
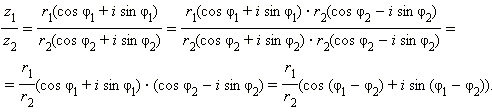 Видно, что в тригонометрической форме операции умножения и деления производятся особенно просто: для того, чтобы перемножить (разделить) два комплексных числа, нужно перемножить (разделить) их модули и сложить (вычесть) их аргументы.
Видно, что в тригонометрической форме операции умножения и деления производятся особенно просто: для того, чтобы перемножить (разделить) два комплексных числа, нужно перемножить (разделить) их модули и сложить (вычесть) их аргументы.
Для возведения в степень используется формула Муавра :
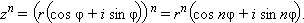
Пример 7. Представить комплексное число 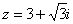 и найти
и найти 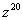 .
.
Самостоятельно представь данной число в тригонометрической форме. Вы должны получить:
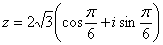
Ввоспользовавшись формулой Муавра, получим:
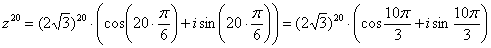
Упростим выражение. Т.к. 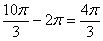 , окончательный ответ :
, окончательный ответ :
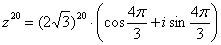 или
или
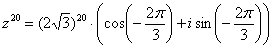
Для того, чтобы извлечь корень из произвольного комплексного числа рассмотрим уравнение 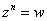 или, то же самое:
или, то же самое: 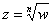 . Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при
. Здесь «эн» может принимать любое натуральное значение, которое больше единицы. В частности, при 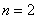 получается квадратный корень
получается квадратный корень 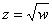
Уравнение вида 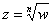 имеет ровно
имеет ровно 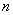 корней
корней 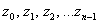 , которые можно найти по формуле:
, которые можно найти по формуле:
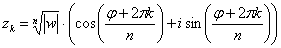 , где
, где 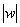 – это модуль комплексного числа
– это модуль комплексного числа 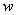 ,
, 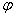 – его аргумент, а параметр
– его аргумент, а параметр 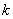 принимает значения:
принимает значения: 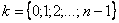
Пример 8.
Найти корни уравнения 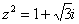
Перепишем уравнение в виде 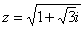
В данном примере 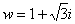 ,
, 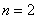 , поэтому уравнение будет иметь два корня:
, поэтому уравнение будет иметь два корня: 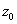 и
и 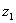 .
.
Общую формулу можно детализировать:
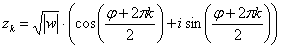 ,
, 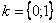
Найдем модуль и аргумент комплексного числа 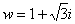 :
:
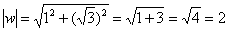
Число 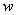 располагается в первой четверти, поэтому:
располагается в первой четверти, поэтому:
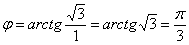
Еще более детализируем формулу:
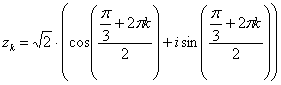 ,
, 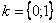
Подставляя в формулу значение 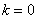 , получаем первый корень:
, получаем первый корень:
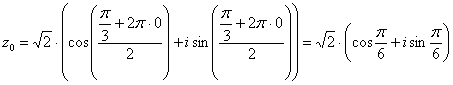
Подставляя в формулу значение 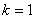 , получаем второй корень:
, получаем второй корень:
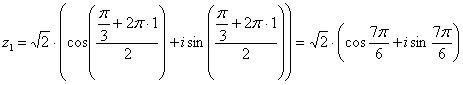
Получаем:
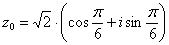 ,
, 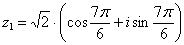
Показательная форма комплексного числа.
Рассматривая функцию y = ex для комплексного переменного Эйлер установил замечательное соотношение
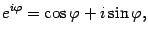
которое носит название формулы Эйлера.
Любое комплексное число (кроме нуля) 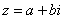 можно записать в показательной форме:
можно записать в показательной форме:
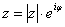 , где
, где 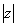 – это модуль комплексного числа, а
– это модуль комплексного числа, а 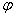 – аргумент комплексного числа.
– аргумент комплексного числа.
Для того , чтобы записать число в показательной форме необходимо найти модуль и аргумент и записать число в виде 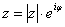 .
.
Пример 9. Число 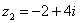 записать в показательной форме. Вычислите самостоятельно модуль и аргумент. Получаться выражения:
записать в показательной форме. Вычислите самостоятельно модуль и аргумент. Получаться выражения:
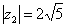 ,
, 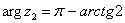 .
.
Тогда данное число в показательной форме запишется следующим образом: 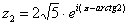 .
.
Над комплексными числами заданными в показательной форме , удобно производить умножение и деление, возведение в натуральную степень и извлечение корня.
Найдем произведение комплексных чисел 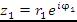 и
и 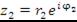 , представленных в показательной форме:
, представленных в показательной форме:
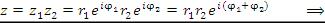
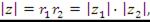
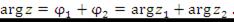
Таким образом, чтобы найти произведение комплексных чисел, нужно перемножить их модули и сложить аргументы.
Аналогично находится деление комплексных чисел 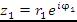 и
и 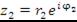 :
:
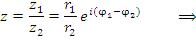
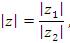
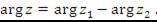
Чтобы разделить одно комплексное число на другое, нужно модуль первого числа разделить на модуль второго и из аргумента первого числа вычесть аргумент второго.
Для возведения в целую степень n комплексного числа  , это число нужно представить в показательной форме, возвести обе части полученного равенства в степень n и записать результат в тригонометрической форме:
, это число нужно представить в показательной форме, возвести обе части полученного равенства в степень n и записать результат в тригонометрической форме: 
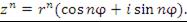
Пример 10. Представить в показательной форме комплексное число 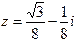 .
.
Решение. Находим модуль числа 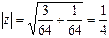 и один из его аргументов
и один из его аргументов 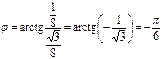
откуда, 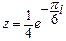 .
.
Решение.
а) Извлеченная стандартная деталь не могла быть утеряна, и значит утеряна одна из остальных 30 деталей (21 + 10 – 1 = 30). Среди них было 20 стандартных (21 – 1 = 20) и 10 нестандартных. Следовательно вероятность события А: Р(А) = 20/30 = 2/3.
б) Легко сообразить, что события А и В противоположны (утеряна либо стандартная, либо нестандартная деталь). Следовательно P(B) = 1-P(A) = 1/3.
5.1.3.1. На стеллаже в случайном порядке расставлены 15 учебников, причем 5 из них по теории вероятностей (ТВ). Наудачу берут три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется по ТВ (событие А).
Решение. Способ 1. Событие А будет реализовано, если произойдет одно из следующих трех несовместных событий:
В – только один из взятых учебников по ТВ;
С – два из трех учебников по ТВ; D – все три учебника по ТВ.
Интересующее нас событие А есть сумма А=В+С+D и по теореме сложения вероятностей получим P(A) = P(B)+P(C)+ P(D)
Найдем вероятности событий В, С и D (см. решение задачи 5.1.1.18):
P(B) = C51.C102/C153 = 45/91; P(C) = C52.C101/C153 = 20/91; P(D) = C53/C153; = 2/91.
Теперь подставим их в выражение для вероятности события А:
P(A) = 45/91 + 20/91 + 2/91 = 67/91
Пример 7. Для сигнализации об утечке ядовитого газа установлены два независимо работающих датчика. Вероятность срабатывания первого из них Р(А) = 0.95, а второго – Р(В) = 0.9. Найти вероятность срабатывания при аварии: а) хотя бы одного датчика; б) только одного датчика.
Решение:
а) Очевидно, что срабатывания датчиков события совместные. Тогда вероятность срабатывания хотя бы одного датчика (событие С) Р(С) = Р(А+В) и Р(А+В) = Р(А)+Р(В) – Р(АВ); Р(АВ) = Р(А).Р(В) = 0.885; Р(С) = 0.95 + 0.9 – 0.885 = 0.995.
б) Пусть событие D означает срабатывание только одного, любого, датчика, тогда 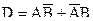 Причем события
Причем события 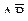 и
и 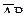 несовместные. Следовательно, по теореме сложения вероятностей имеем:
несовместные. Следовательно, по теореме сложения вероятностей имеем: 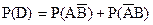 и, применив теорему умножения вероятностей для независимых событий (срабатывания первого и второго датчиков события независимые), получим
и, применив теорему умножения вероятностей для независимых событий (срабатывания первого и второго датчиков события независимые), получим 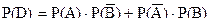
 = 0.95.0.1 + 0.9.0.05 = 0.14.
= 0.95.0.1 + 0.9.0.05 = 0.14.
Вопросы для самопроверки
1.Что такое частота случайного события? Как частота связана с вероятностью?
2. Какие значения может принимать вероятность случайного события?
3. Какие события называют достоверными? Чему равна вероятность достоверных событий?
4. Какие события называют невозможными? Чему равна вероятность невозможного события?
5. Приведите примеры невозможных и достоверных случайных событий.
6.. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекают 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными. (Отв. 24/91)
7. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей нет бракованных. (Отв.0,65)
8. Приведите примеры маловероятных событий. Подумайте, какими из них можно, а какими нельзя пренебрегать в одном испытании.
9. Укажите, какие из перечисленных событий, по вашему мнению, являются достоверными, а какие — невозможными:
а) монета, брошенная на гладкую жесткую поверхность, встала на ребро;
б) на игральном кубике кости выпало 7 очков;
в) на игральном кубике выпало от одного до шести очков;
г) номер открытой страницы в книге — дробное число;
10. Являются ли достоверными события:
а) на игральной кости выпало четное число очков;
б) на игральной кости выпало целое число очков?
11. Вычислить: А104; Р4; С104.
12. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекают 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными. (Отв. 24/91)
13. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей нет бракованных. (Отв.0,65)
14. Составить закон распределения дискретной случайной величины Х – числа появлений «герба» при двух бросаниях монеты.
15. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение дискретной случайной величины Х, заданной законом распределения: а) Х -4 6 10; б) Х 0.21 0.54 0.61
Р 0.2 0.3 0.5 Р 0.1 0.5 0.4
Вопросы и упражнения для самопроверки:
- Дайте определение комплексного числа.
- Дайте определение мнимй единицы.
- Как найти степень мнимой единицы?
- Какие комплексные числа называются равными, сопряжеными?
- Как изображаются комплексные числа геометрически?
- Дайте определение модуля и аргумента комплексного числа.
- Перечислите формы записи комплексного числа.
- Как выполняются действия над комплексными числами, заданными в алгебраической форме; в тригонометрической форме; в показательной форме?
- Найдите модульи аргумент комплексного числа z=-2+2ί√3.Комплексное число, изображенное точкой (2, -2), запишите во всех трех формах.
- Запишите в тригонометрической форме комплексные числа: а) z=-√3+ί; б) z=-1+ί√3.
- Представьте в показательной форме комплексные числа: а) z=-√2-ί√2; б) z=5ί.
Задания контрольной работы.
Вычислить предел функции.
| 1. | 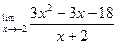
| 14. | 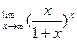
|
| 2. | 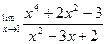
| 15. | 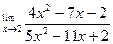
|
| 3. | 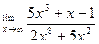
| 16. | 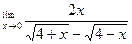
|
| 4. | 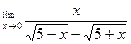
|
| |
| 5. | 
| ||
| 6. | 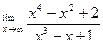
| ||
| 7. | 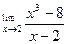
| ||
| 8. | 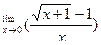
| ||
| 9. | 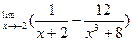
| ||
| 10. | 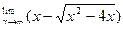
| ||
| 11. | 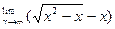
| ||
| 12. | 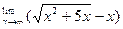
| ||
| 13. | 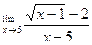
| ||
17.Решить уравнение.
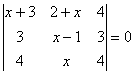 .
.
18- 21.Решить систему методом Крамера:
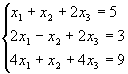
19.
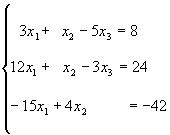
20.

3х +2y + z =3
5x - 2y - 2z = 3
x + y - z = -2
21.

5х +8y + z = 2
3x - 2y + 6z = -7
2 x + y - z = -5
22.Решить систему матричным способом
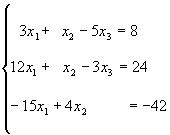
23.Решите систему уравнений при различных значениях параметра p: 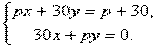
24.Решить систему уравнений, составив матричное уравнение.

3х +2y + z =3
5x - 2y - 2z = 3
x + y - z = -2
25. Решить систему уравнений методом Гаусса.

5х +8y + z = 2
3x - 2y + 6z = -7
2 x + y - z = -5
Вычислить интеграл.
| 51. | 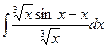
| 64. | 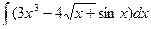
|
| 52. | 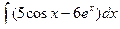
| 65. | 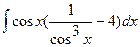
|
| 53. | 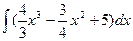
| 66. | 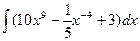
|
| 54. | 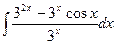
| 67. | 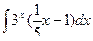
|
| 55. | 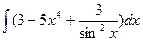
| 68. | 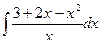
|
| 56. | 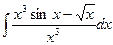
| 69. | 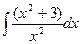
|
| 57. | 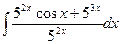
| 70. | 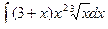
|
| 58. | 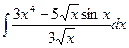
| 71. | 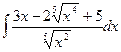
|
| 59. | 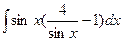
| 72. | 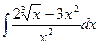
|
| 60. | 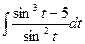
| 73. | 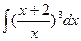
|
| 61. | 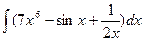
| 74. | 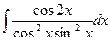
|
| 62. | 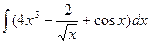
| 75. | 
|
| 63. | 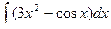
|
Выполните решение задач.
101. Шеститомное собрание сочинений Н. В. Гоголя поместили на полку б случайном порядке. Какова вероятность того, что тома стоят в порядке возрастания номеров?
102. Из урны, содержащей 8 шаров, помеченных цифрами 1, 2, 3, 4, 5, 6, 7, 8, вынимают наугад все шары один за другим. Найдите вероятность того, что номера извлеченных шаров, будут идти в порядке возрастания.
103.Карточка «Спортлото» содержит 49 чисел.. В тираже участвуют б чисел. Какова вероятность того, что верно будет угадано 6 чисел?
104.Брошена игральная кость. Какова вероятность того, что выпадет нечетное число очков? что выпадет «шестерка»?
105.Из пяти букв разрезной азбуки составлено слово «крыша». Ребенок рассыпал буквы и собрал в произвольном порядке. Найдите вероятность того, что у него ошва получится слово «крыша».
106.Карточка «Спортлото» содержит 36 чисел. В тираже участвуют 5 чисел. Какова вероятность того, что верно будет угадано 5 чисел?
107. Имеется 100 деталей, из которых возможны 4 %' бракованных. Какова вероятность того, что взятая наугад деталь—бракованная?;
108.Восемь различных книг расставляются наугад на одной полке. Какова вероятность того, что три определенные книги окажутся поставленными рядом?
109.Карточка «Спортлото» содержит 49 чисел. В тираже участвуют 6 чисел. Какова вероятность того; что верно будет угадано 5 чисел?
110.На карточках разрезной азбуки написано 32 буквы алфавита. Пять карточек вынимают наугад одну за другой и укладывают, на стол в порядке появления. Какова вероятность того, что получится слово «хорда»?
111.В урне 7 красных и 6 синих шаров. Из урны наугад вынимаются два шара. Найдите вероятность того, что они разного цвета.
112.Карточка «Спортлото» содержит 36 чисел. В тираже участвуют 5 чисел. Какова вероятность того, что верно будет угадано 4 числа?
113.Из группы, состоящей из 10 юношей и 8 девушек, выбирают по жребию 4 дежурных. Какова вероятность того, что в числе избранных окажутся двое юношей и дне девушки?
114.Экзаменационные билеты пронумерованы от 1 до 35. Какова вероятность того, что наудачу взятый билет имеет номер, кратный пяти?
115.Карточка «Спортлото» содержит 49 чисел, В тираже участвуют 6 чисел. Какова вероятность того, что верно будет угадано 4 числа?
116.Из семи одинаковых карточек разрезной азбуки «а», «к», «н», «о», «с», «у», «ф» наудачу выбирают 5 карточек и складывают их в ряд в порядке извлечения. Какова вероятность получить при этом слово «конус»?
117. На прилавке книжного магазина лежит 10 различных книг, причем 5 книг стоят по 1 руб. каждая, 3 книги — по 3 руб. и 2 книги — по 4 руб. Найдите вероятность того, что взятые наугад две книги стоят 5 руб.
118.Карточка «Спортлото» содержит 36 чисел. В тираже участвуют 5 чисел. Какова вероятность того, что верно будет угадано 3 числа?
119.Из числа шаров, занумерованных всеми двузначными числами, наудачу берется один. -Какова вероятность того, что номер взятого шара-оканчивается нулем?
120.На шести одинаковых карточках написаны буквы «а», «з», «и», «м», «п», «p. Карточки перемешивают и раскладывают наудачу в ряд. Какова вероятность того, что получилось слово «призма»?
121. Брошены две игральные кости. Найти вероятность следующих событий: а) сумма выпавших очков равна семи (событие А); б) сумма выпавших очков равна восьми, а их разность – четырем (событие В); в) сумма выпавших очков равна пяти, а их произведение – четырем (событие С).
122. На складе имеется 15 телевизоров, причем 10 из них фирмы SONY. Найти вероятность того, что из пяти наудачу выбранных телевизоров, три окажутся от SONY.
123. В ящике 10 деталей, из которых четыре окрашены. Наудачу из ящика взяли 3 детали. Найти вероятность того, что хотя бы одна из них окажется окрашенной. 224. В урне 5 белых, 20 красных и 10 черных шаров, не отличающихся по размеру. Шары тщательно перемешивают и затем наугад вынимают 1 шар. Какова вероятность того, что вынутый шар окажется белым или черным?
124. Ведутся поиски двух преступников. Каждый из них независимо от другого может быть обнаружен в течение суток с вероятностью 0,5. После поимки одно из них, в связи с увеличением количества сотрудников, занятых в поисках, вероятность найти второго возрастает до 0,7. Какова вероятность того, что в течение суток будет обнаружены оба преступника.
125. На складе имеется 15 телевизоров, причем 10 из них фирмы SONY. Найти
вероятность того, что из пяти наудачу выбранных телевизоров, три окажутся от SONY.
Литература
- «Алгебра и начало анализа», под ред. Г.Н. Яковлева, М.: 1981 г. ч. I.
- «Алгебра и начало анализа», под ред. Г.Н. Яковлева, М.: 1981 г. ч. II.
- И.И. Валуцэ, Г.Д. Дилигул «Математика для техникумов», М.: Просвещение, 2005 г.
- Н.В. Богомолов «Практические занятия по математике», М.: Просвещение, 2005 г.
- Ш.А. Алимов, Ю.М. Колягин «Алгебра и начала анализа. Учебник для 10-11 классов средней школы», – М.: Просвещение, 2008 г.
специальность: 19.02.10 «Технология продукции общественного питания» 1 курс
Дата: 2019-03-05, просмотров: 400.