Обозначим lj - трудоемкость единицы j-го продукта. Для обеспечения валового выпуска X необходимо количество труда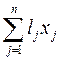 
Если ресурсы труда L заданы, то задачу можно решать только для тех у, для которых хватает труда, то есть любой конечный спрос удовлетворить нельзя, так как может не хватить труда:
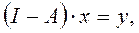
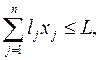
где In - единичная матрица размером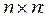 
А - квадратная матрица технологических затрат.
Если структура конечного спроса задана, например:
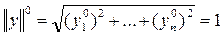
тогда при заданной технологии А и ограниченных ресурсах труда L задача максимизации конечного спроса в заданной структуре 
сводится к максимизации а.
max a
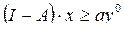
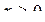
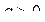
ТЕМА 9 МОДЕЛИ ВЗАИМОДЕЙСТВИЯ ПОТРЕБИТЕЛЕЙ И ПРОИЗВОДИТЕЛЕЙ
Паутинообразная модель
Модель Эванса
Модель Вальраса
В этом разделе рассмотрим модели установления равновесной цены и модель Вальраса, в которой при определенных условиях можно достичь общего конкурентного равновесия.
Методы установления равновесной цены основаны на предположении, что изменение цены зависит от разности спроса и предложения, если спрос выше предложения, то цена возрастает, в противном случае - убывает (это паутинообразная модель и модель Эванса).
Модель Вальраса рассматривает экономическую систему, в которой производится, распределяется и потребляется большое число товаров. Число потребителей и производителей конечно, но настолько велико, что ни один из них не может влиять на цены.
Паутинообразная модель
Функция спроса на товар является убывающей функцией цены, а функция предложения однопродуктовой фирмы, полученная при максимизации прибыли, -возрастающая функция цены.
Рассмотрим рынок с одним продуктом. Спрос на этот продукт характеризуется убывающей функцией совокупного спроса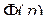 
, а предложение - возрастающей функцией совокупного предложения 
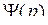. Эти функции определены и непрерывны для любого p > 0. Кроме этого считаем, что
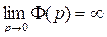
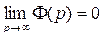
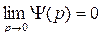
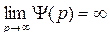
Состояние равновесия имеет вид:
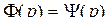(1)
и имеет единственное решение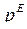 
, то есть
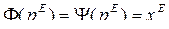
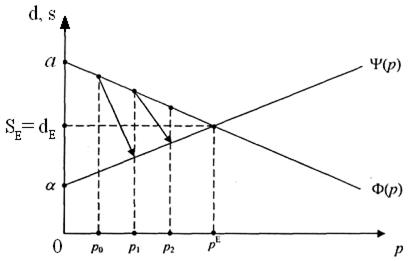
Паутинообразная модель позволяет реализовать процесс приближения к равновесной цене. Пусть в начальный момент времени установлена начальная цена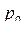 
, при этом спрос оказался меньше предложения
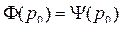
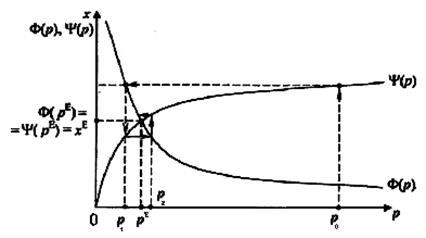
Шаг 1. Понижаем цену до уровня, при котором спрос равен предложению при первоначальной цене:
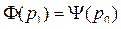
При новой цене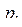 
спрос превышает предложение:
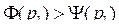
Шаг 2. Понижаем цену до уровня р2, при котором:
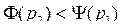
и т.д.
На рисунке видно, что процесс, описываемый рекуррентным соотношением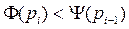 
сходится (функция 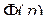- выпуклая, 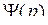- вогнутая).
Если бы 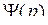была выпуклой, то процесс расходился бы при единственном решении.
Модель Эванса
Рынок одного товара. Время t - непрерывно.
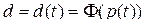- совокупный спрос в момент времени t.
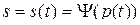- совокупное предложение в момент времени t.
р = p(t) - цена товара.
Спрос и предложение - линейные функции цены.
| (1) |
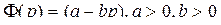, спрос с ростом цены убывает
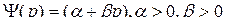, предложение с ростом цены растет
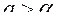- при нулевой цене спрос превышает предложение. Основное предположение при моделировании, что изменение цены пропорционально превышению спроса над предложением.
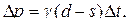
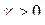(2)
Согласно выражению (2) взаимодействие потребителей и производителей таково, что цена непрерывно возрастает, если спрос превышает предложение и падает в противном случае.
Перейдем от выражения (2) к дифференциальному уравнению относительно цены:
; 
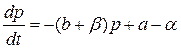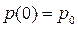(3)
Решение уравнения в точке равновесия (рЕ).
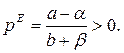(4)
Из выражения (3) видно, что при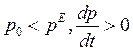 
и, наоборот, при 
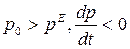, поэтому 
.
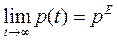В первом случае цена достигает равновесного значения возрастая, во втором случае - убывая. При этом равновесная цена совершенно не зависит от р0 -начальной. Равновесная цена - абсцисса точки пересечения прямых спроса и предложения.
В дискретном аналоге время разбито на промежутки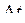 
, цена в момент 
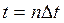равна:
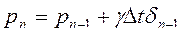
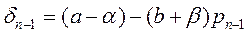(5)
Выводы, сделанные для дискретной модели, такие же, как и для решения дифференциального уравнения (3).
Решение уравнение (3) выглядит следующим образом:
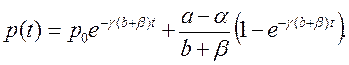
Модель Вальраса
Концептуальная схема модели основана на следующем: каждый из участников экономической системы стремится достичь своих функционалов цели, поэтому возможны конфликты.
Для нормального функционирования всей системы необходимо согласовать стратегии структурных единиц между собой.
В модели Вальраса, имеющей конечное число потребителей и производителей, такое решение конфликта достигается регулированием системы цен.
Если структуры не влияют на цены, то рынок называют конкурентным.
Основная идея Вальраса в определении системы цен, обеспечивающей распределение ресурсов и продуктов на основе разделения конфликтов между участниками.
Такая равновесная ситуация называется конкурентным равновесием.
Рассмотрим рынок с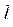 
потребителями 
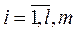производителями 
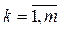и n типами товаров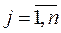 
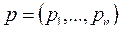- вектор-строка цен, 
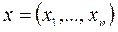- вектор-столбец товаров).
Товар - это предмет потребления, продукт труда, средство труда (оборудование, здания и т.д.), первичные ресурсы (труд и природные ресурсы).
Каждый потребитель обладает доходом К(р) и имеет поле предпочтения товаров, заданное в виде функции полезности u(х). Если обозначить х(р) - множество возможных наборов товаров, доступных потребителю при ценах p , Х- область определения u(х), то функция спроса потребителей задается:
|
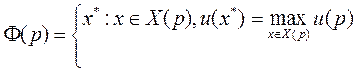(1)
т.е. функция спроса - это множество доступных наборов товаров, каждый из которых максимизирует полезность (потребителей) при заданных ценах p.
Каждый потребитель характеризуется функцией спроса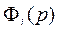 
и доходом 
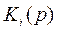. Доход складывается из двух частей:
1) доходов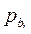 
от продажи первоначального запаса 
;
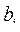2) дохода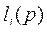 
в результате участия потребителя в производстве.
Таким образом,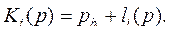 
.
В векторе-столбце затрат-выпуска k-го производителя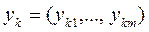 
положительные компоненты соответствуют выпуску, а отрицательные - затратам.
Множество производственных возможностей ук - это множество всех допустимых векторов затрат-выпуска.
Под функцией предложения фирмы понимают один или несколько векторов затрат-выпуска, которые при заданных ценах р максимизируют прибыль.
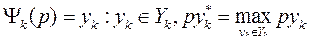(2)
Вектор затрат всей системы: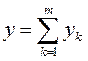 
.
При таком суммировании компоненты вектора затрат-выпуска взаимно сокращаются, т.к. они положительны для производителей, и отрицательны для потребителей промежуточных продуктов.
В итоге в вектор у войдут с положительным знаком конечные продукты, с отрицательным - первичные ресурсы.
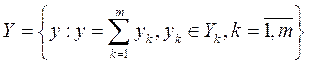
Распределение производства осуществляется выбором вектора затрат-выпуска yk из технологического множества производственных возможностей Yk для каждого производителя k = 1, ..., m. Сумма 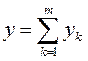представляет собой совокупный производственный процесс.
Такие совокупные процессы образуют совокупное технологическое множество Y (общеэкономическое множество производственных мощностей).
Сумма по всем потребителям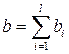 
представляет совокупную первоначальную собственность.
В понятие начальной собственности входят потребительские товары, промежуточные продукты (предметы труда), капитальное оборудование (средства труда), земля и другие природные ресурсы, труд.
Множество {b} + Y — множество совокупного предложения.
Сумма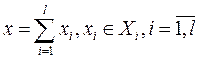 
- вектор совокупного спроса. Некоторые компоненты вектора могут быть отрицательными, если они представляют собой предложение (например, труда).
Под совместным распределением производства и потребления понимается такой набор векторов потребления и векторов затрат-выпуска,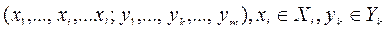 
, для которого совокупный спрос совпадает с совокупным предложением:
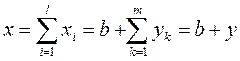. (3)
Набор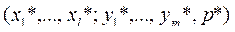 
задает конкурентное равновесие в модели Вальраса, если
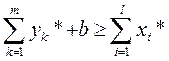(5)
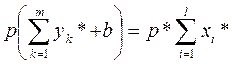(6)
При этом p* называется вектором конкурентных цен.
Соотношения (5), (6) называют законом Вальраса в широком смысле, если же в выражении (5) имеет место равенство, то это закон Вальраса в узком смысле.
Таким образом, конкурентное равновесие представляет собой совместное распределение производства и потребления, при котором совокупный спрос не превосходит совокупного предложения (5), стоимость совокупного спроса в конкурентных ценах равна стоимости конкурентного предложения в этих же ценах (6), при этом каждый потребитель максимизирует свою полезность в ценах p *, а каждый производитель - свою прибыль в этих же ценах (4).
Таким образом, существование конкурентного равновесия означает существование такой системы равновесных (конкурентных) цен p *, при которых согласуются конфликтные интересы потребителей и производителей.
Дата: 2019-03-05, просмотров: 220.
