Главными условиями существования системы управления являются следующие:
1. Организованность: в системе управления выделяются элементы, которые относятся либо к управляющей, либо к управляемой подсистеме:
S= S1 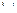 S2
S2
2. Разнообразие: каждая из двух выделенных подсистем должна допускать возможность появления нескольких (многих) состояний:
х 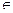 Х, y
Х, y 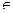 Y, m
Y, m 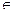 M, X
M, X 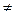 Æ, Y
Æ, Y 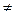 Æ, M
Æ, M 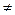 Æ
Æ
Примечание: проблема оценки разнообразия управляющей системы и ее соотношения с разнообразием управляемого объекта имеет важное теоретическое и практическое значение.
Закон необходимого разнообразия формулируется У. Р. Эшби следующим образом: «количество исходов управляемой системы, если оно минимально, может быть еще уменьшено только за счет соответствующего увеличения разнообразия управляющей системы». Это значит, что для решения задачи управления необходимо, чтобы информационная мощность управляюцугй системы (или ее собственное информационное разнообразие) была не меньше разнообразия объекта управления (т. е. решаемой задачи управления).
Пусть в дискретные моменты времени t = 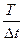 происходит изменение вектора х (t) входов объекта управления, а управляющая система вырабатывает вектор m(t) управляющих воздействий, в результате которых состояние объекта управления определяется как u(t)=γ(х(t),л(t),·). Перевод управляемого объекта из состояния и (t) в некоторое состояние u(t+ 1) требует решения задачи прогнозирования x(t + 1), оценки параметров системы, решения задачи идентификации u(t), выбора подходящего m(t + 1):
происходит изменение вектора х (t) входов объекта управления, а управляющая система вырабатывает вектор m(t) управляющих воздействий, в результате которых состояние объекта управления определяется как u(t)=γ(х(t),л(t),·). Перевод управляемого объекта из состояния и (t) в некоторое состояние u(t+ 1) требует решения задачи прогнозирования x(t + 1), оценки параметров системы, решения задачи идентификации u(t), выбора подходящего m(t + 1):
u(t +1) = φ(x(t + l),m(t + 1),u(t),·).
Если разнообразие задачи управления, измеряемое количеством информации, определить как V, а информационную мощность управляющей системы Ж, то для осуществления перехода u(t)→u(t + 1) необходимо, чтобы в каждый момент времени t выполнялось условие W(t)³V(t).
В реальных системах управления «полное» разнообразие объекта управления и воздействий внешней среды настолько велико, что последнее условие, вообще говоря, не выполняется. Поэтому управляющая система формирует гомоморфную модель, использует прин цип управления воздействием на «главный» фактор, прибегая к агрегированию, линеаризации связей, аппроксимируя стохастические зависимости детерминированными и проч. Часто воздействия неучтенных в моделях факторов вводятся в модель с помощью так называемого «внешнего дополнения». Согласно концепции Ст. Вира, некий «черный ящик» служит дополнением к модели объекта управления, функционируя в качестве блока неформализуемых решений, рандомизатора — датчика случайных чисел и внося поправки в модельные расчеты. Таким образом, принцип «внешнего дополнения» обеспечивает реализацию системного подхода, учет влияния внешней среды, открытый характер системы управления, поскольку «замкнутая система не способна, отправляясь от различных начальных условий, достигать определенных целей».
3. Динамичность:
x(t) 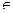 X,u(t)
X,u(t) 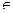 U,y(t)
U,y(t) 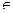 Y,
Y,
m(t) 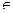 M, ω(t)
M, ω(t) 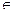 Ω, t
Ω, t 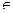 T,
T,
где Т—упорядоченное числовое множество.
4. Наличие прямых и обратных связей, обеспечивающих причинно-следственные зависимости в системе управления:
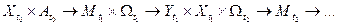
t0<t1<t2<… (3.4)
5. Наличие цели управления, достижение которой является макрофункцией управляемой системы:
Φ=Φ(y). (3.5)
Цель системы в зависимости от ее характера задается различным образом. Для систем, работа которых завершается достижением цели, требуется, чтобы у (t) достигло целевого множества 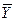 . В частном случае, чтобы выполнялось условие y(t) =
. В частном случае, чтобы выполнялось условие y(t) = 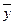
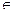
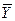 . Для других систем необходимо, чтобы у (t) достигла области
. Для других систем необходимо, чтобы у (t) достигла области 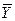 , а затем продолжала движение по траектории y’(t)
, а затем продолжала движение по траектории y’(t) 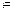
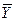 или не выходила из области
или не выходила из области 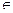
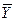 .
.
6. Управляемость: можно найти такое управляющее воздействие т, которое за конечное число шагов переведет систему в искомое состояние, обеспечивающее достижение цели:
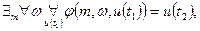 (3.6)
(3.6)
такое, что ψ(u(t2)) = 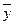 ,
,
гдеt1 ≤ t2, t1, t2 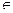 T,
T,
φ, ψ — соответственно функция переходов и функция выхода системы,
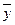 - количественное выражение цели,
- количественное выражение цели, 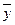
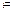 Y.
Y.
Введение понятия управляемости системы вызывает необходимость рассмотрения вопросов качества управления и его эффективности.
Пусть 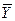 - некоторое заданное целевое множество:
- некоторое заданное целевое множество:
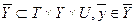 , (3.7)
, (3.7)
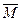 - множество допустимых управлений.
- множество допустимых управлений.
Если управляющее воздействие 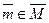 преобразует некоторое исходное событие (t0, u0) в (t1, u1,)
преобразует некоторое исходное событие (t0, u0) в (t1, u1,) 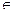
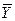 и t1 - время первого достижения, то t1; называется моментом достижения, а разность (t1 - t0) - временем достижения.
и t1 - время первого достижения, то t1; называется моментом достижения, а разность (t1 - t0) - временем достижения.
Вещественное число, вычисляемое как некоторый функционал:
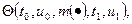 (3.8)
(3.8)
где u1, = 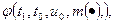 y1=ψ (t1, u1)называется качеством управления m(·) относительно начального события (t0, u0) .
y1=ψ (t1, u1)называется качеством управления m(·) относительно начального события (t0, u0) .
Определение 3.2: абстрактной задачей управления называется сложное математическое понятие, образованное совокупностью:
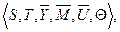 (3.9)
(3.9)
где S — динамическая система,
Т— множество моментов времени,
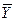 – целевое множество,
– целевое множество, 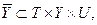
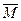 - множество допустимых управлений,
- множество допустимых управлений,
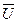 - подмножество множества
- подмножество множества 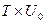 (начальных событий),
(начальных событий),
Q - функционал качества управления;
с поставленным требованием: «для каждого начального события (t0,u0) 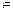
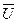 определить некоторое допустимое управление m(·)
определить некоторое допустимое управление m(·) 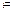
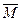 , которое переводит (t0,х0) в
, которое переводит (t0,х0) в 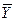 и при этом минимизирует функционал
и при этом минимизирует функционал 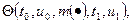 , где t1 - момент первого достижения, а u1 -точка первого достижения множества
, где t1 - момент первого достижения, а u1 -точка первого достижения множества 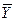 ».
».
Определение 3.2 является весьма общим, однако служит базой для дальнейшего исследования необходимых условий оптимальности систем управления. Выяснение вопросов существования оптимального решения и поиска такого решения является содержанием математической теории управления (теория Гамильтона-Якоби, принцип максимума Понтрягина, методы функционального анализа, ряд численных методов).
Определение 3.3: рассмотрим произвольную динамическую систему S. Законом управления называется отображениеx: ТхU → X, ставящее в соответствие каждому состоянию u{t) и каждому моменту времени t значение x(t) = x (t, u(t)) входного воздействия в этот момент времени.
При этом другие параметры динамической системы S могут влиять на конкретный вид функции x.
Принцип, в соответствии с которым входные воздействия должны вычисляться через состояния, был сформулирован Ричардом Беллманом, указавшим на его первостепенную важность. В этом принципе заключена важнейшая идея теории управления. Это научная интерпретация принципа «обратной связи», составляющего основу любого управления.
Важно отметить, что в текущем состоянии системы содержится вся информация, необходимая для определения требуемого управляющего воздействия, поскольку, по определению динамической системы, будущее поведение системы полностью определяется его нынешним состоянием и будущими управляющими воздействиями.
Оптимальное управление заключается в выборе и реализации таких у правлений и е U, которые являются наилучшими с точки зрения эффективности достижения цели управления.
Можно выделить два основных типа критериев эффективности систем управления.
Критерий эффективности первого рода — степень достижения цели системой. Если цель системы задана областью цели 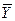 или точкой
или точкой 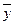
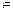 Y, то критерием эффективности I рода является отклонение р, определяемое в терминах
Y, то критерием эффективности I рода является отклонение р, определяемое в терминах 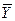 . Цель считается достигнутой, если
. Цель считается достигнутой, если
p(y(t) 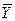 ) = 0 или p(y(t),
) = 0 или p(y(t), 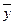 )<e, (3.10)
)<e, (3.10)
где e - заданная малая величина.
При задании целевой функции
F{y(to),y’(t))→extr,
y(to) 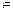 Y,y'(t)
Y,y'(t) 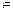 Y, (3.11)
Y, (3.11)
если существует F* = extr F, критерий I рода — разность (F* -F).
Критерий эффективности второго рода — оценка эффективности траектории движения системы к цели. Он определяется как некоторая функция:
f(x, u, y)→ extr (3.12)
Критерий II рода позволяет сравнивать и оценивать различные изменения состояний системы в ходе достижения цели. Так, улучшение работы системы по критерию второго рода позволяет достичь цели при лучших значениях входов: обеспечить выпуск того же количества продукции 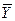 при меньших затратах факторов производства Х; или при лучших значениях состояний системы: минимальном времени непроизводительного простоя системы, минимуме отходов и брака и т. д.
при меньших затратах факторов производства Х; или при лучших значениях состояний системы: минимальном времени непроизводительного простоя системы, минимуме отходов и брака и т. д.
В ряде случаев могут быть использованы критерии третьего типа — смешанные, в которых отражается сочетание приведенных показателей эффективности пути и степени достижения цели системой.
Дата: 2019-03-05, просмотров: 341.