Производственная функция - это зависимость результата производства от затрат ресурсов.

Обозначим ресурсы через 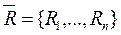, годовой объем производства различных видов продукции - 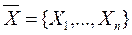. В качестве ресурсов обычно рассматривают накопленный труд в виде производственных фондов (капитал) K и сам труд 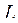; результат производства - валовой выпуск  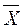(либо валовой внутренний продукт 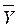, либо национальный доход ).

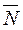Накопленный труд (K) проявляется в основных и оборотных, производственных и непроизводственных фондах. Выбор того или иного состава K определяется целью исследования.

Итак, модель экономики в виде производственной функции:

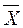= F(K,L).

Рассмотрим экономическую интерпретацию основных характеристик ПФ на примере мультипликативной функции (Кобба-Дугласа) и других ПФ, используемых в экономике.

Производственная функция 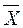= F(K,L) называется неоклассической, если она гладкая и удовлетворяет следующим условиям:

1. F (0, L) = F(К, 0) = 0 - при отсутствии одного из ресурсов производство невозможно;

2. 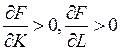 - с ростом ресурсов выпуск растет;

3. 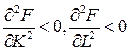 – с увеличением ресурсов скорость роста выпуска замедляется;

4. 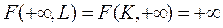 – при неограниченном увеличении одного из ресурсов выпуск неограниченно растет.

Мультипликативная ПФ задается выражением:

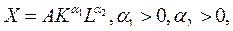                          (1)

где А - коэффициент нейтрального технического прогресса;

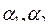 – коэффициенты эластичности по труду и фондам.

ПФ обладает свойством (1): при отсутствии одного из ресурсов производство невозможно.

Частным случаем функции (1) является функция Кобба-Дугласа:

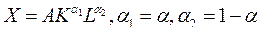,                          (2)

Эластичность выпуска по основным фондам — это:

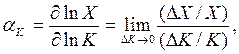                             (3)

Эластичность выпуска по труду:

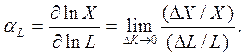                            (4)

Прологарифмируем (2):

Tак как 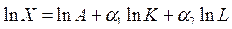, то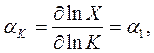

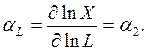
Из (3) видно, что коэффициент эластичности показывает, на сколько процентов увеличится выпуск, если ресурс возрастет на 1%.

Например, мультипликативная функция валового выпуска в зависимости от стоимости основных производственных фондов и числа занятых в народном хо­зяйстве за 34 года по СССР:

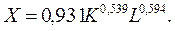
Это означает, что при увеличении ОФ на 1% валовой выпуск увеличится на 0,539%, а при увеличении занятых на 1% - на 0,594%.

Если 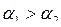, то это трудосберегающий (интенсивный) рост.

Если 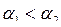, то это фондосберегающий (экстенсивный) рост.

Мультипликативная функция определяется по временному ряду выпусков и затрат ресурсов 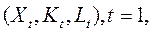T, где T - длина временного ряда.

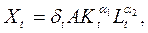                                     (5)

где 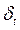 - корректировочный случайный коэффициент, который приводит в соответствие фактический и расчетный выпуск и отражает флюктуацию результата под воздействием других факторов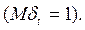

Логарифмируя (5), получаем модель линейной множественной регрессии, где параметры А, 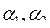определяются методом НК:

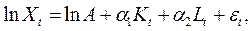                            (6)

где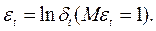

Мультипликативная функция удовлетворяет второму условию: с ростом затрат ресурсов выпуск увеличивается.

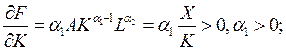
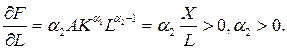
Из этого условия следует, что предельная фондоотдача пропорциональна средней фондоотдаче 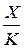 с коэффициентом 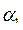, а предельная производительность труда - средней производительности труда  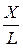с коэффициентом .

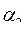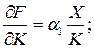
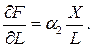
При 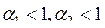 предельные отдачи факторов меньше средних.

Условие 3 для мультипликативной функции :

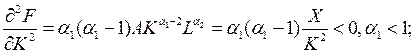
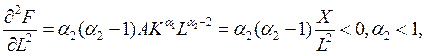
т.е. с ростом затрат ресурса его предельная отдача падает.

Условие 4 видно из выражения 1, т.е. при неограниченном увеличении одного из ресурсов выпуск неограниченно растет. При 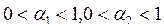 мультипликативная функция является неоклассической.

Рассмотрим темп роста выпуска.

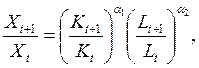                                 (7)

Возведя обе части (7) в степень 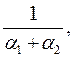 получим следующее:

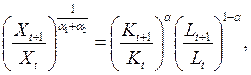                         (8)

где 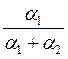;  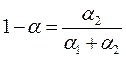– относительные эластичности факторов.

В (8): выражение справа - среднее геометрическое темпа роста затрат ресурсов.

При 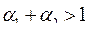 выпуск растет быстрее 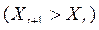, чем в среднем растут факторы  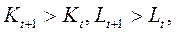значит при :

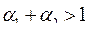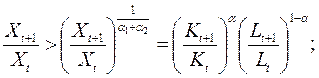
т.е. темп выпуска больше среднего темпа роста факторов.

Вывод. При 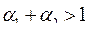 производительная функция описывает растущую экономику.