Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Методы регулирования основаны на использовании обратной связи. Рассмотрим простую систему регулирования, имеющую один вход X и выход Y(рис.3.4).

Имеется некоторая регулируемая система S, которая подвергается определенным воздействиям X, дающим в итоге требуемый результат Y.

Результат воздействует на регулятор R, который, в свою очередь, воздей­ствует на регулируемую систему. Комплекс регулируемой системы и регу­лятора составляет систему регулирования. Преобразование состояния входа X в состояние выхода Y формально можно отобразить как: Y = SX. Этот способ отображения соответствует разомкнутому контуру управле­ния. Как показано на рис. 3.4, состояние выхода регулируемой системы S передается на вход регулятора R, выходом которого является величина АХ. Это состояние прибавляется к состоянию входа системы S: X + ΔХ.

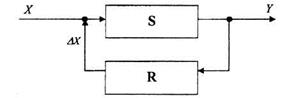
Рисунок 3.4 Система регулирования

Предположим, что регулируемая система работает как пропорцио­нальный преобразователь: Y= SX.

При S > 1 пропорциональное преобразование называется усилением, а при S < 1 - ослаблением.

Показатель S= 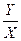 называется пропускной способностью регулируемой системы.

Предположим также, что регулятор тоже осуществляет пропорцио­нальное преобразование, а его пропускная способность равна R. Тогда ΔХ = RY. С учетом воздействия регулятора состояние выхода регулируемой системы определится как:

Y = S(X + ΔХ) = S(X + RY) = SX + SRY.

Отсюда

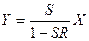.                   (3.15)

Выражение (3.15) является основной формулой теории регулирова­ния. Приведенная формула дает возможность рассчитать необходимое зна­чение входной величины, чтобы при заданных параметрах системы S и R получить на выходе искомый результат У. Принимая во внимание то, что 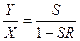, выражение  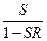называется пропускной способностью системы регулирования. Из основной формулы теории регулирования вытекает специфическая роль регулятора. При R = 0 пропускная способ­ность регулируемой системы была бы равна S: Y = SX. Наличие регулятора требует введения множителя 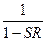, который характеризует его действие. Сомножитель  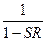выражает действие обратной связи в системе регулирования, и его называют оператором или мультипликатором обрат­ ной связи.

Регулирование как функция управления получила широкое примене­ние в исследовании экономических систем управления.

Основные свойства и характеристики регулируемых систем изуча­ются технической кибернетикой в разделе теории автоматического управ­ления.

Адаптивное управление

В тех случаях, когда воздействующие на систему факторы являются частично или полностью неопределенными, управление становится воз­можным только после накопления некоторой информации об этих факто­рах и характеристиках объекта. Управление в системе с полной априорной информацией об управляемом процессе, которое изменяется по мере нако­пления информации и применяется для улучшения качества работы систе­мы, называется адаптивным управлением.

В дискретном времени t = 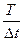, где Т — время, Δt — интервал его квантования, процесс адаптивного управления может быть представлен следующим образом. Пусть управляемый процесс и является марковским процессом и описывается некоторой характеристикой информации Р.

Марковский процесс — случайный процесс, обобщенное понятие динамической системы, введенное А. Н. Колмогоровым, процесс, который обладает тем свойством, что его поведение после момента t зависит только от его значения в этот момент и не зависит от поведения процесса до момента t.

Пусть в момент t заданы состояние процесса u_t и состояние инфор­мации о процессе P_t образующие точку (x_t P_t) в некотором фазовом про­странстве. Переход в новое состояние происходит под воздействием управления x_t и возмущения ω(t) случайной величины с вероятностным распределением dP{u_t, P_t; x_t ω(t)), которое может являться какой-то частью характеристики информации. Переход в новое состояние может быть оп­ределен случайными преобразованиями 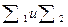 так, что:

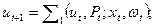      (3.16)

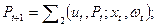     (3.17)

Управление x, изменяя состояние процесса и, влияет и на характери­стику информации Р.

Если преобразования 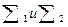заданы, то управление в момент пере­хода следует выбирать в виде:

x_t=x_t(u_t , P_t)                                                             (3.18)

Управление (3.18) обладает свойством адаптации в том смысле, что оно зависит от всей доступной в момент t информации P_t о процессе. Но обычно преобразования 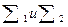 не заданы, и определение этих преобразова­ний, как и самой характеристики информации, является частью задачи об управлении с адаптацией. Для того чтобы информация о процессе со вре­менем накапливалась, необходимо специально выбирать  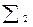так, чтобы описание процесса Р_t+1 было более полным, чем Pt Изменения в направле­нии улучшения характеристик информации составляют сущность адапта­ции. Если с состоянием u_t+1 связать некоторый показатель качества управ­ления Q(u_t+1), то за счет большей «информированности» управления вследствие адаптации этот показатель может улучшаться. При этом после­довательность преобразований ( 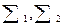), t = 0,1,2,... дает процесс управ­ления с адаптацией.

Таким образом, общее представление процесса адаптивного управ­ления включает характеристику информации Р и механизм адаптации, оп­ределяемый преобразованием .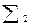

Двойственный характер адаптивного управления проявляется в том, что, с одной стороны, невозможно осуществлять эффективное управление, не зная характеристик объекта, с другой — можно изучать эти характери­стики в процессе управления и тем самым улучшать его. Управляющие воздействия носят двойственный характер: они служат средством как ак­тивного познания управляемого объекта, так и непосредственного управ­ления им в текущий момент времени.

В системах адаптивного управления обязательным является наличие обратной связи ввиду непрерывного процесса исследования характеристик объекта.

В системах управления, реализующих принцип адаптации, могут меняться параметры и структура системы (самоорганизация), программа, алгоритм функционирования и управляющие воздействия (самонастрой­ ка). Накопление и обобщение опыта обеспечивает возможности обучения и самообучения систем управления.

Адаптивное управление в полной мере присуще системам управле­ния в живой природе. Она дает нам образцы совершенной организации, настройки и функционирования систем управления сложнейшими динами­ческими процессами, которые современная теория и практика управления стремиться воспроизвести в искусственных системах. Адаптация в экономических системах проявляется в способности системы сохранять в про­цессе развития существенные параметры не изменяющимися в определен­ных границах их варьирования, несмотря на разнообразие воздействий внешней среды.

Управление – это такое входное воздействие или сигнал в результате которого система ведет себя заданным образом.

Различают три способа управления в зависимости от того, на основе какой информации формируется управленческий сигнал:

1. Управление по отклонению:

где ОУ – объект управления;

Р – орган, вырабатывающий управляющее воздействие;

u – управляющее воздействие;

e – разность (отклонение) желаемого и фактического результата;

w – вход;

y – выход.

Данный способ управления используется в замкнутых системах. Замкнутая система управления позволяет быстро реагировать на нежелательные отклонения в поведении объекта с целью устранения этих отклонений. Однако она не следит за причинами, вызвавшими эти отклонения. Отсюда возникает проблема – неустойчивость совместного функционирования объекта управления и системы.

Преимущество замкнутой системы в том, что она обеспечивает достижение цели управления, когда возмущающих воздействий много и не все они могут быть измерены, или же заранее не известны влияния этих возмущений.

2. Управление по возмущению или нагрузке.

Использует сведения о возможных воздействиях на управляемый объект со стороны окружающей среды. Этот способ управления характеризует разомкнутая система, которая учитывает причины возмущающих воздействий среды, но не оценивает результата фактического действий этих возмущений.

3. Комбинированное управление.

Является сочетанием двух предыдущих способов управления – управления по отклонению и управления по возмущению (нагрузке).

Имеется четыре основные задачи управления:

· стабилизация;

· программное управление;

· слежение;

· оптимальное управление.

Стабилизация системы – это поддержание ее выходных показателей вблизи заданных значений.

Программное управление – это поддержание выходных показателей вблизи заданных значений, зависящих от времени заданным образом.

Слежение – это обеспечение как можно более точного соответствия между состоянием или поведением объекта управления и состоянием или поведением какого-либо другого объекта, которым управлять невозможно.

Оптимальное управление – при нем нужно наилучшим образом выполнить задачу, стоящую перед объектом при заданных условиях и ограничениях.

 

ПРЕЗЕНТАЦИЯ 6

 ТЕМА 7. МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ ПРОИЗВОДСТВЕННЫХ ФИРМ ДЛЯ МАКСИМИЗАЦИИ ПРИБЫЛИ

1. Описание поведения производственных фирм на функциональном уровне.

2. Определение максимального выпуска однопродуктовой фирмы, заданной производственной функцией Кобба-Дугласа:

 

Пусть производственная фирма выпускает один вид продукции или много видов, но в постоянной структуре, тогда обозначим X - годовой выпуск фирмы в натурально-вещественной форме (т.е. число единиц продукции одного вида или число многономенклатурных агрегатов).

Для производства продукции используется труд L - среднее число занятых в год, либо отработанные за год человеко-часы, и прошлый труд К в виде средств труда (основные производственные фонды) и предметы труда М (затраченные за год топливо, энергия, сырье, комплектующие и т.д.).

Каждый из этих трех агрегированных видов ресурсов (труд, фонды и материалы) имеет определенное число разновидностей (труд разной квалификации, оборудование различного вида и т.п.).

Обозначим вектор-столбец возможных объемов затрат различных видов ресурсов через х = (х₁,...,х_n). Тогда технология фирмы определяется ее производственной функцией, отражающей связь между затратами и выпуском:

X = F ( x ).

Функция F ( x ) непрерывная, дважды дифференцируемая и неоклассическая, т.е. гладкая и удовлетворяющая условиям:

1. F (0, L) = F (К, 0) = 0 - при отсутствии одного из ресурсов производство невозможно;

2. 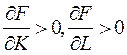 – с ростом ресурсов выпуск растет;

3. 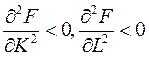 – с увеличением ресурсов скорость роста выпуска замедляется.

Кроме того, матрица вторых производных функции F ( x ) определена.

Если цена единицы продукции - Р, а цена единицы ресурса j-го вида -W_j, 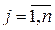, то каждому вектору затрат х отвечает прибыль:

П(x) = pF(x) – Wx                                       (1)

Цены ресурсов имеют естественный смысл:

¾ если х _j - среднегодовое число занятых определенной профессии, то W_j - годовая зарплата одного работника данной профессии;

¾ если х _j - покупные материалы (топливо, энергия и т.д.), то W_j – покупная цена единицы данного материала;

¾ если х _j - производственные фонды определенного вида, то W_j - годовая арендная плата за единицу фондов или стоимость поддержания единицы фондов в исправности, если фирма владеет этими средствами.

В выражении (1) 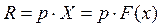 - стоимость годового выпуска фирмы (или ее годовой доход);  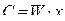- издержки производства или стоимость затрат фирмы за год.

Если нет других ограничений на размеры ресурсов, кроме их неотрицательности, то задача на максимизацию прибыли имеет вид:

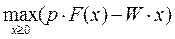                                  (2)

Это задача нелинейного программирования с п условиями неотрицательности 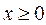. Необходимое условие ее решения является выполнение условий Куна-Таккера:

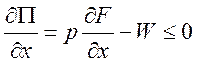
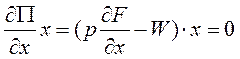                        (3)

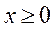
в точке х^* – оптимум

 

Если в оптимальном решении использованы все виды ресурсов, а х^* > 0, то условие (3) имеет вид:

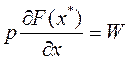, или                                          (4)

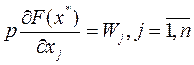
т.е. в предельной

Такое же по форме решение имеет задача на максимум выпуска при заданном объеме издержек:

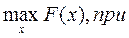
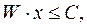                                                       (4a)

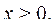
Это задача нелинейного программирования с одним линейным ограничением и условием неотрицательности переменных.

Для решения такой задачи строится функция Лагранжа, или вспомогательный функционал:

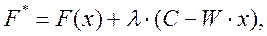
затем ищут его максимум при условии неотрицательности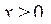

Для этого необходимо выполнение условий теоремы Куна-Таккера:

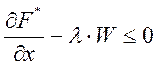
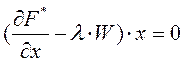                           (5)

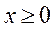
Эти условия совпадают с условиями (3), если где 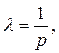где р - цена единицы продукции.

Пример.

Определить максимальный выпуск однопродуктовой фирмы, заданной производственной функцией Кобба-Дугласа:

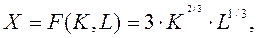                        (5a)

если на аренду фондов и оплату труда выделено 150 ден. ед.,

стоимость аренды единицы фондов W_K = 5 ден. ед./ед. фондов,

ставка заработной платы WL = 10 ден.ед./чел.

Какова предельная норма замены одного занятого фондами в оптимальной точке?

Решение.

Т.к. F (0, L) = F (К, 0) = 0, то в оптимальной точке 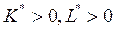. Условия (5) имеют вид:

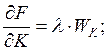
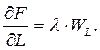                                               (6)

Для производственной функции (5а):

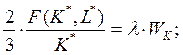
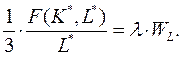
Разделив первое уравнение на второе, получим:

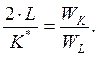
Подставив это соотношение в уравнение ограничения 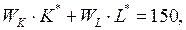 найдем:

  

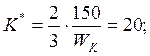
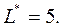
Графически решение имеет вид:

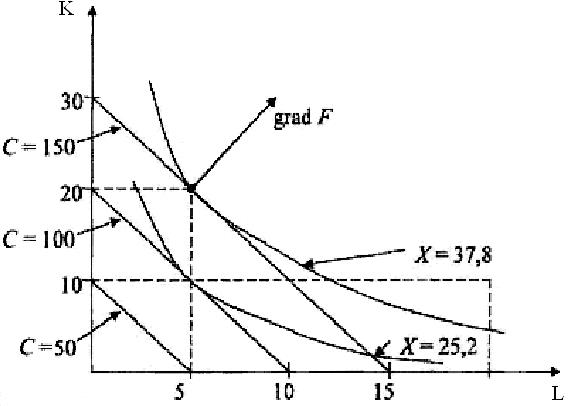
а) линии постоянных издержек С- изокосты;

б) линии постоянных выпусков для Х= 25,2; Х= 37,8 - изокванты.

Изокосты описываются уравнением:

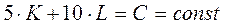
Изокванты описываются уравнением:

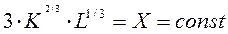
В оптимальной точке 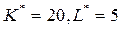 изокванта X = 37,8 и изокоста С = 150, проходящие через эту точку, касаются, т.к. по (6) нормали к этим кривым, заданные градиентами 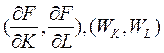коллинеарны.

Норма замены труда фондами в оптимальной точке:

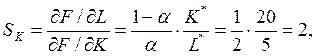
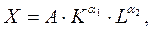
где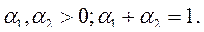

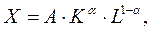
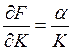 – предельный продукт фондов;

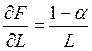 – предельный продукт труда (производительность труда).

Решая задачу фирмы (2):

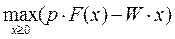
находим оптимальный набор ресурсов X* > 0; этому набору отвечает одинаковое значение издержек .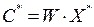

Решим теперь задачу на максимум прибыли при заданных издержках (4а).

Если F(x) - неоклассическая функция, то в оптимальном решении 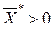, причем это решение единственно. Таким образом, с одной стороны:

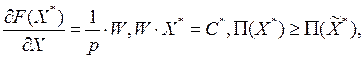
с другой:

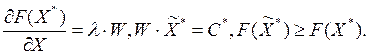
Поскольку:

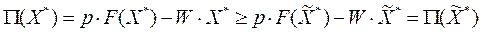
и 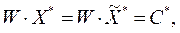 то

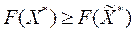, но 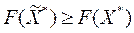поэтому

.

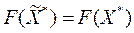Т.к. решение задачи (2) единственно, то .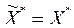

Таким образом, если задача на максимум прибыли имеет единственное ре­шение X* > 0, то ей отвечает задача на

причем последняя имеет такое же решение как и

Геометрическое место точек касания изокост и изоквант при разных значениях издержек С определяет долгосрочный путь развития фирм Х(С), т.е. показывает, как будет увеличиваться (уменьшаться) выпуск, если издержки возрастут (или уменьшатся).