Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Раздел 4. Начала математического анализа.

Тема 4.1. Последовательности

 

Вариант 1

1. Исследовать функцию 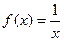 на непрерывность в точке .

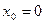2. Вычислить приращение данной функции, если ее аргумент x получает приращение :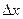

, , .

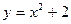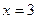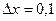3. Сумма первого и четвертого членов убывающей геометрической прогрессии относится к сумме второго и третьего членов этой же прогрессии, как 13:4. Найти первый член прогрессии, если ее третий член равен 32.

 

Вариант 2

1. Исследовать функцию 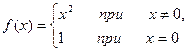 на непрерывность в точке .

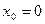2. Вычислить приращение данной функции, если ее аргумент x получает приращение :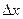

, , .

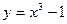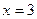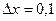3. Сумма членов бесконечно убывающей геометрической прогрессии равна 56, а сумма квадратов ее членов равна 448. Найти эту прогрессию.

 

Вариант 3

1. Исследовать функцию 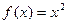 на непрерывность в точке .

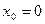2. Вычислить приращение данной функции, если ее аргумент x получает приращение :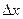

, , .

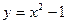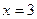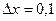3. В квадрат, сторона которого равна 76 см, вписан другой квадрат, вершины которого являются серединами сторон первого квадрата, в этот квадрат вписан таким же образом другой квадрат и т.д. (см. рис.). Найти сумму площадей всех квадратов.

Пакет преподавателя

 

Вариант 1

 

1. Решение.

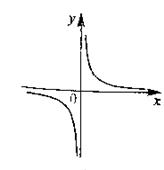
Проверим условия из определения.

1) 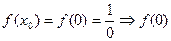 не существует, т. е. функция  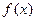неопределенна в точке 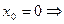функция  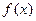не является непрерывной в точке .

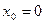Ответ. Не является непрерывной.

 

Вариант 2

 

1. Решение.

Проверим условия из определения.

1) 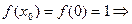 функция  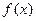определенна в точке .

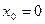2) 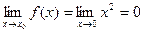. Функция  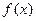имеет конечный предел при .

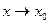3) 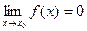, 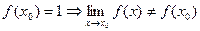. Предел функции при  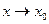не равен значению функции в этой точке.

Ответ. Не является непрерывной.

 

Вариант 3

 

1. Решение.

Проверим условия из определения.

1) 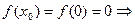 функция  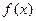определенна в точке .

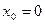2) 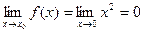. Функция  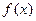имеет конечный предел при .

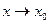3) 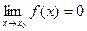, 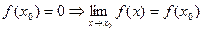. Предел функции при  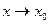равен значению функции в этой точке.

Ответ. Непрерывна.

 

 

http://www.yaklass.ru/p/algebra/9-klass/progressii-9139/geometricheskaia-progressiia-9142/re-f5f4ff72-963f-4b86-aece-3bb6086df8dc

 

ОЦЕНОЧНОЕ СРЕДСТВО № 12

КОМПЛЕКТ ЗАДАНИЙ ДЛЯ письменного тестирования

Раздел 4. Начала математического анализа.

Тема 4.2. Производная

 

1. Найдите производную функции f(x) = 4x-5.

a) 4                                  б) 9                                           в) -5

2. Найдите производную функции f(x) = 6x⁴-3x³-2x²-8.

а) 6х³-3х²-2х                          б) 24х³-9х²-2х²-8              в) 24х³-9х²-4х

3. Найдите производную функции f(x) = 5x³-4 .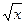

а) 15x²-4                         б) 15x²- 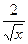                      в) 15x²-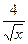

4. Найдите производную функции f(x) = .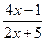

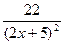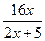а)                     б)                              в)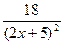

5. Найдите производную функции f(x) = xcosx.

а) cosx+xsinx                         б) sinx+xcosx               в) cosx-xsinx

6. Найдите производную функции .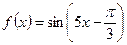

а) 5cos5x                        б) 5sin(x- 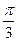)               в) 5cos(5x- )

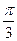7. Найдите производную функции: f(x) = (1+3x)²⁰.

а) (1+3x)¹⁹                      б) 20(1+3х)¹⁹               в) 60(1+3х)¹⁹

8. Дана функция f(x) = x²-4x. Найдите значение производной в точке х = 4.

а) 12                           б) 4                                      в) 8

9. Найдите 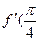), если f(x) = 3cosx.

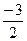
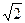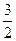
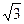а)                        б)                                 в)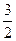

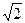
10. Найдите точки, в которых значение производной функции равно нулю.

a) х = -1; x = 7                б) x = -7; x = 1                         в) 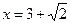; x = 3-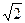

Пакет преподавателя

№ вопроса	1	2	3	4	5	6	7	8	9	10
правильный ответ	а	в	б	а	а	в	в	б	а	а

ОЦЕНОЧНОЕ СРЕДСТВО № 13