Раздел 4. Начала математического анализа.
Тема 4.3. Первообразная и интеграл
| I вариант | II вариант |
| № 1. Найти следующие неопределенные интегралы: | № 1. Найти следующие неопределенные интегралы: |
1) 
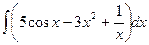
| 1)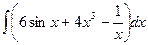 
|
2) 
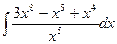
| 2)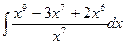 
|
3) 
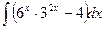
| 3)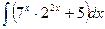 
|
4) 
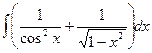
| 4)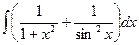 
|
5) 
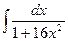
| 5)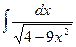 
|
| № 2. Вычислить следующий определенный интеграл: | № 2. Вычислить следующий определенный интеграл: |
 .
|  .
|
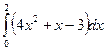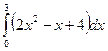| № 3. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной следующими линиями: | № 3. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной следующими линиями: |
| 
|
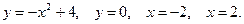
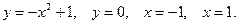
ОЦЕНОЧНОЕ СРЕДСТВО № 16
КОМПЛЕКТ ЗАДАНИЙ ДЛЯ проверочной работы
Раздел 5. Геометрия.
Тема 5.1. Прямые и плоскости в пространстве
Вариант 1
- Выполните чертеж к задаче. Прямые а, в, и с имеют общую точку О, но не существует плоскости, в которой лежат все эти три точки.
- Выполните чертеж к задаче. Плоскость α проходит через середины сторон АВ и АС ΔАВС и не содержит вершины А.
- Прямая АВ пересекает плоскость α в точке О, расстояние от точки А до плоскости равно 4 см. Найдите расстояние от точки В до плоскости, если точка О середина АВ.
Вариант 2
- Выполните чертеж к задаче. Прямые а, в, и с имеют общую точку О и лежат в одной плоскости.
- Выполните чертеж к задаче. Прямая а параллельна каждой из параллельных плоскостей α и β.
- Прямая АВ пересекает плоскость α в точке О, расстояние от точки А до плоскости равно 4 см. Найдите расстояние от точки В до плоскости, если точка В середина ОА.
Вариант 3
- Выполните чертеж к задаче. Прямые СД и СК пересекают плоскость β в разных точках.
- Выполните чертеж к задаче. Прямая АВ параллельна плоскости γ, а прямая АТ пересекает ее в точке Т.
- Прямая АВ пересекает плоскость α в точке О, расстояние от точки А до плоскости равно 4 см. Найдите расстояние от точки В до плоскости, если точка А средина ОВ.
Вариант 4
- Выполните чертеж к задаче. Две вершины ΔАВС лежат в плоскости γ, а вершина С не лежит в плоскости γ. Прямая d пересекает стороны СВ и СК соответственно в точках М и Т, а плоскость α в точке К.
- Выполните чертеж к задаче. Плоскость α пересекает три параллельных прямых соответственно в точках А, В, и С, лежащих на одной прямой.
- Прямая АВ пересекает плоскость α в точке О, расстояние от точки А до плоскости равно 4 см. Найдите расстояние от точки В до плоскости, если ОА = 8 см, АВ = 6 см.
ОЦЕНОЧНОЕ СРЕДСТВО № 17
КОМПЛЕКТ ЗАДАНИЙ ДЛЯ контрольной работы
Раздел 5. Геометрия.
Тема 5.2. Координаты и векторы
Вариант 1
1. Даны два вектора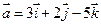 
и 
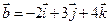. Вычислить координаты и длину векторов 
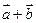и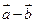 
.
2. Найти площадь треугольника по координатам его вершин: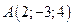 
, 
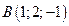и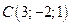 
.
3. Даны векторы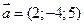 
и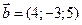 
. Вычислить косинус угла между ними.
4. Найти скалярное произведение векторов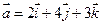 
и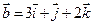 
.
5. Даны векторы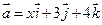 
и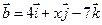 
. При каком значении 
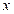векторы 
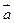и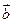 
перпендикулярны?
6. Вектор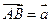 
задан координатами своих концов: 
, 
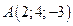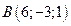. Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами 
.
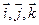Вариант 2
1. Даны два вектора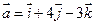 
и 
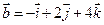. Вычислить координаты и длину векторов 
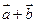и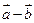 
.
2. Найти площадь треугольника по координатам его вершин: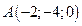 
, 
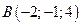и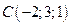 
.
3. Даны векторы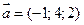 
и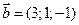 
. Вычислить косинус угла между ними.
4. Найти скалярное произведение векторов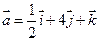 
и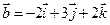 
.
5. Даны векторы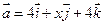 
и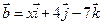 
. При каком значении 
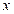векторы 
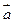и 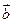перпендикулярны?
6. Вектор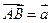 
задан координатами своих концов: 
, 
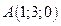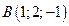. Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами 
.
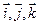Вариант 3
1. Даны два вектора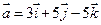 
и 
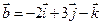. Вычислить координаты и длину векторов 
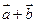и .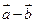
2. Найти площадь треугольника по координатам его вершин: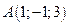 
, 
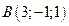и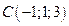 
.
3. Даны векторы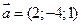 
и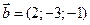 
. Вычислить косинус угла между ними.
4. Найти скалярное произведение векторов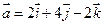 
и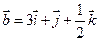 
.
5. Даны векторы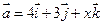 
и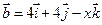 
. При каком значении 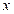векторы 
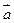и 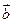перпендикулярны?
6. Вектор 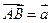задан координатами своих концов: 
, 
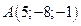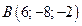. Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами 
.
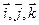Вариант 4
1. Даны два вектора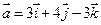 
и 
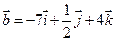. Вычислить координаты и длину векторов 
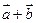и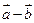 
.
2. Найти площадь треугольника по координатам его вершин: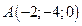 
, 
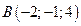и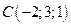 
.
3. Даны векторы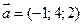 
и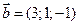 
. Вычислить косинус угла между ними.
4. Найти скалярное произведение векторов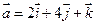 
и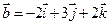 
.
5. Даны векторы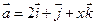 
и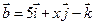 
. При каком значении 
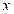векторы 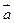и 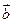перпендикулярны?
6. Вектор 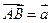задан координатами своих концов: 
, 
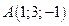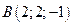. Вычислить его длину и косинусы углов, которые образует вектор с единичными векторами 
.
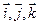ОЦЕНОЧНОЕ СРЕДСТВО № 18
Дата: 2019-03-05, просмотров: 1385.
