Мета завдання: Навчитися систематизувати первинну інформацію, використовуючи зведення та метод простого групування статистичних даних.
Зміст завдання: У відповідності із варіантом завдання утворити ряди розподілу робітників підприємства:
a) за віком;
b) за величиною загального робочого стажу;
c) за неперервним стажем роботи на даному підприємстві;
d) за кваліфікаційним розрядом;
e) за розміром заробітної плати.
Таблиця 1.1
Вибір варіантів завдання
| Перша літера прізвища студента | А-Е | Є-Й | К-П | Р-Х | Ц-Я |
| Номери завдань, які необхідно виконати | a | b | c | d | e |
&
Отримані в результаті статистичного спостереження дані потребують упорядкування, систематизації та наукової обробки. З цією метою здійснюють їх зведення – загальне упорядкування даних, підрахунок кількості обстежених одиниць сукупності у відповідності із завданням аналізу.
Подальше групування статистичних даних передбачає розподіл статистичної сукупності на групи за однією або більше ознаками. В результаті здійснюється певна узагальнена оцінка одиниць сукупності та їх систематизація. Групування за однією ознакою називають простим групуванням.
Як привило, при групуванні за кількісною ознакою постає питання щодо кількості груп. Якщо досліджувана ознака має невелику кількість варіантів, то кількість груп визначається за принципом зручності, наприклад, груп може бути стільки, скільки існує варіантів досліджуваної ознаки. В такому випадку переважно формується дискретний ряд розподілу – ряд, в якому досліджувані ознаки виражені окремим цілим числом.
Якщо досліджувана ознака характеризується великою кількістю варіантів, то кількість груп доцільно визначати за формулою Стерджеса:
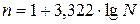 (1.1)
(1.1)
де N – кількість одиниць сукупності.
При цьому формується інтервальний ряд розподілу із представленням групувальної ознаки у вигляді інтервалу. Величина інтервалу визначається за формулою:
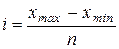 (1.2)
(1.2)
де x max і x min – відповідно найбільше і найменше значення ознаки.
В загальному випадку, ряд розподілу – це впорядкований розподіл одиниць статистичної сукупності за групувальною ознакою. Він складається із варіантів (значень групувальної ознаки) і частот (числа, що показують скільки разів повторюються окремі значення групувальної ознаки). Накопичену частоту називають кумулятивною частотою.
Графічно дискретний ряд розподілу зображується у вигляді полігону, інтервальний ряд розподілу можна зображати як у вигляді гістограми, так і у вигляді полігону (при цьому точками з’єднань є середини інтервалів). Накопичену частоту графічно зображають у вигляді кумуляти.
Послідовність виконання завдання:
1. Використовуючи первинні дані індивідуального завдання сформувати вихідну таблицю статистичних даних для характеристики робітників підприємства за заданою ознакою.
Таблиця 1.2
Вихідна таблиця статистичних даних
| № з/п | Назва ознаки | № з/п | Назва ознаки | № з/п | Назва ознаки |
| 1 | 54 | 107 | |||
| 2 | 55 | 108 | |||
| … | … | … | |||
| 53 | 106 | 159 |
2. Сформувати таблицю впорядкованих даних для характеристики робітників підприємства за заданою ознакою. Для цього потрібно впорядкувати статистичні дані за зростанням досліджуваної ознаки. Результати представити в табл. 1.3.
Таблиця 1.3
Таблиця впорядкованих даних
| Назва ознаки | № з/п | Назва ознаки | № з/п | Назва ознаки | № з/п |
| … | … | … | |||
| … | … | … |
3. Побудувати інтервальний (дискретний) ряд розподілу робітників підприємства за досліджуваною ознакою. Для цього потрібно:
- розрахувати кількість груп та величину інтервалу групування;
- провести підрахунок кількості робітників у кожному інтервалі групування та їх загальну кількість;
- провести підрахунок накопиченої кількості робітників підприємства.
Результати переставити в табл. 1.4.
Таблиця 1.4
Дата: 2019-03-05, просмотров: 488.