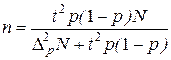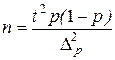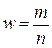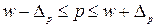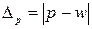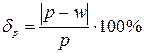Мета завдання: Навчитися розрахувати чисельні характеристики статистичної сукупності на основі методу вибіркового спостереження
Зміст завдання: У відповідності із варіантом завдання розрахувати за допомогою методу вибіркового спостереження визначити:
a) частку робітників у віці до 30 років, при умові, щоб гранична похибка вибірки не перевищувала 4% з ймовірністю 0,89;
b) частку робітників, загальний трудовий стаж яких перевищує 30 років, при умові, щоб гранична похибка вибірки не перевищувала 3% з ймовірністю 0,68;
c) частку робітників, неперервний стаж роботи яких на даному підприємстві перевищує 20 років, при умові, щоб гранична похибка вибірки не перевищувала 5% з ймовірністю 0,89;
d) частку робітників, які мають 3 кваліфікаційний розряд, при умові, щоб гранична похибка вибірки не перевищувала 4% з ймовірністю 0,68;
e) частку робітників, заробітна плата яких перевищує 680 грн., при умові, щоб гранична похибка вибірки не перевищувала 3% з ймовірністю 0,68.
Таблиця 4.4
Вибір варіантів завдання
| Перша літера прізвища студента | А - Е | Є - Й | К - П | Р - Х | Ц - Я |
| Номери завдань, які необхідно виконати | c | b | e | d | a |
&
Основними завданнями проведення вибіркового спостереження є визначення середнього розміру досліджуваної ознаки (див. завдання 1 лабораторної роботи № 4) та визначення частки досліджуваної ознаки у певній сукупності.
При здійсненні вибіркового спостереження для визначення частки досліджуваної ознаки актуальними є всі теоретичні положення, описані у завданні 1 лабораторній роботі № 4. Обсяг вибірки визначається при
| безповторному відборі: | повторному відборі: |
|
|
|
| (4.7) |
де N – обсяг генеральної сукупності;
Δx – гранична похибка вибірки для заданої ймовірності Р;
t – довірче число (коефіцієнт довіри) для заданого значення ймовірності Р (визначається на основі табличних даних Додатку В);
p – частка одиниць сукупності, які мають певні значення ознаки (p = M/N, де M – кількість одиниць, які мають певні значення ознаки);
(1- p ) – частка одиниць сукупності із протилежним значенням ознаки;
p (1- p ) – дисперсія частки, значення якої можна розрахувати за результатами завдання 1 лабораторної роботи № 1.
Для формування вибіркової сукупності способом простого випадкового безповторного відбору доцільно скористатись можливостями програмного пакету Excel (див. завдання 1 лабораторної роботи № 4.)
Частка вибіркової сукупності обчислюється за формулою:
|
| (4.8) |
де m – кількість одиниць, які мають певні значення ознаки
Результат проведеного вибіркового спостереження записується у вигляді довірчого інтервалу:
|
| (4.9) |
Для порівняння отриманих результатів із показниками генеральної сукупності доцільно визначити абсолютну і відносну похибки вибірок.
Абсолютна похибка вибірки обчислюється за формулою:
|
| (4.10) |
де p - частка ознаки генеральної сукупності (p = M/N, де M – кількість одиниць, які мають певні значення ознаки), w – частка ознаки вибіркової сукупності.
Відносна похибка вибірки обчислюється за формулою:
|
| (4.11) |
Порівняння обчисленої відносної похибки із її граничним значенням дозволяє зробити висновок про точність проведеного вибіркового спостереження: якщо відносна похибка менша за її граничне значення, то точність спостереження є задовільною і отримані результати дозоляють характеризувати досліджувані параметри генеральної сукупності.
Послідовність виконання завдання:
1. Використовуючи первинні дані індивідуального завдання представити генеральну сукупність статистичних даних у вигляді таблиці 4.5.
Таблиця 4.5
Генеральна сукупність даних для дослідження (вказати назву ознаки)
| № з/п | Назва ознаки | № з/п | Назва ознаки | № з/п | Назва ознаки |
| 1 | 54 | 107 | |||
| 2 | 55 | 108 | |||
| … | … | … | |||
| … | … | … | |||
| 52 | 105 | 158 | |||
| 53 | 106 | 159 |
2. Визначити обсяг вибірки для проведення вибіркового статистичного дослідження.
3. Сформувати вибіркову сукупність способом простого випадкового безповторного відбору. Представити сформовані вибіркову сукупність у вигляді таблиці 4.6.
Таблиця 4.6
Дата: 2019-03-05, просмотров: 459.