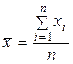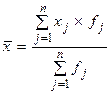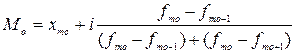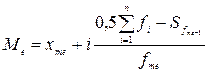Мета завдання: Навчитися визначати та аналізувати статистичні характеристики центру розподілу статистичної сукупності
Зміст завдання: У відповідності із варіантом завдання 1 лабораторної роботи № 1 розрахувати статистичні характеристики центру розподілу статистичної сукупності: середню, моду, медіану.
&
Для характеристики центру розподілу статистичної сукупності використовуються такі показники як середня величина, мода та медіана.
Середня величина – це одна із основних характеристик, які використовуються у статистичному аналізі. Вона є узагальнюючою мірою ознаки, що варіює у статистичній сукупності. Її величина показує рівень даної ознаки у розрахунку на одиницю сукупності.
Середня величина характеризує типовий рівень значень ознаки і відображає те спільне, що об’єднує масу елементів сукупності. Вона поглинає індивідуальні відмінності одиниць сукупності і виявляє загальні (характерні) значення на одиницю сукупності.
Одним із видів середньої величини є середня арифметична, що розраховується за простою формулою (якщо дані не згруповані) і за зваженою формулою (якщо дані згруповані).
Проста формула розрахунку середньої арифметичної:
|
| (3.1) |
де хі – варіанта (значення) ознаки; n – обсяг сукупності.
Зважена формула розрахунку середньої арифметичної:
|
| (3.2) |
де f j – частота значень ознаки у j-тій групі сукупності.
До характеристик центру розподілу належать також мода і медіана. Їх часто називають порядковими середніми. На відміну від середньої арифметичної, що є абстрактною величиною, ці характеристики завжди збігаються із конкретними варіантами. В окремих випадках вони мають переваги перед середньою арифметичною і використовуються при вирішенні деяких практичних питань.
Мода – це значення ознаки, яке найчастіше зустрічається у статистичні сукупності. У дискретному ряді розподілу модальне значення ознаки знаходять за найбільшою частотою. Зустрічаються полімодальні ряди, що мають більше, ніж одну моду. Для визначення моди у інтервальному ряді розподілу використовується наступна формула:
|
| (3.3) |
де xmo та і – відповідно нижня межа та ширина модального інтервалу;
fmo, fmo-1, fmo+1 – частоти модального, передмодального та післямодального інтервалів.
Медіана – це значення ознаки, яке припадає на середину впорядкованого за зростанням чи спаданням ряду розподілу і ділить його на дві рівні частини, при цьому кількість значень які менші або рівні дорівнює кільності значень, які більші або рівні. Для визначення медіани використовують кумулятивні частоти. У дискретному ряді медіаною буде значення ознаки, для якого кумулятивна частота (сума накопичених частот) дорівнює або перевищує половину суми усіх частот. Для визначення медіани у інтервальному ряді використовується наступна формула:
|
| (3.4) |
де xmе та і – відповідно нижня межа та ширина медіанного інтервалу;
Σf – сума частот ряду розподілу;
Sfme-1 – сума накопичених частот до медіанного інтервалу;
fm e – частота медіанного інтервалу.
Послідовність виконання завдання:
1. Проведений у завданні 1 лабораторній роботі № 1 розподіл робітників підприємства за досліджуваною ознакою представити у вигляді таблиці 3.1.
Таблиця 3.1
Розподіл робітників підприємства за (вказати назву ознаки)
| Назва ознаки | Середина інтервалу, х j | Кількість робітників, осіб f j | Накопичена кількість робітників, осіб d j |
| … | |||
| … | |||
| … | |||
| Разом | - |
2. Для утвореного варіаційного ряду визначити наступні статистичні характеристики центру розподілу:
- середнє арифметичне,
- моду,
- медіану.
3. Зробити висновки за результатами аналізу.
GКонтрольні питання
1. Які показники використовуються для характеристики центру розподілу статистичної сукупності?
2. В чому полягає важливе значення середньої величини у статистичному аналізі?
3. Як розраховується середня арифметична для згрупованих та незгрупованих даних?
4. В чому полягає відмінність порядкових середніх від середньої арифметичної?
5. Що таке мода? Як вона розраховується для дискретного та інтервального рядів розподілу?
6. Що таке медіана? Як вона розраховується для дискретного та інтервального рядів розподілу?
Дата: 2019-03-05, просмотров: 377.