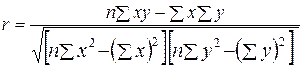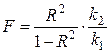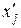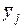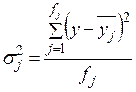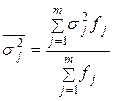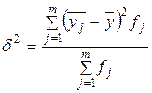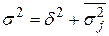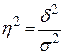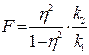МЕТОДИЧНІ ВКАЗІВКИ
до виконання лабораторних робіт
для студентів напряму підготовки 6.030601 – „Менеджмент”
спеціальності „Менеджмент організацій і адміністрування”
Затверджено
на засіданні кафедри
менеджменту організацій
Протокол № 9 від 11.03.2010 р.
Львів – 2010
Статистика: Методичні вказівки до виконання лабораторних робіт для студентів напряму підготовки 6.030601 – „Менеджмент” спеціальності „Менеджмент організацій і адміністрування” / Укл.: О.З.Сорочак, О.Б.Стернюк, Я.В.Панас. – Львів: Видавництво Національного університету „Львівська політехніка”, 2010. – 55 с.
Укладачі: Сорочак О.З., канд. техн. наук, доц.
Стернюк О.Б., асист.
Панас Я.В., асист.
Відповідальний за випуск: Чухрай Н.І., докт. екон. наук, проф.
Рецензенти: Войцеховська Ю.В., канд. екон. наук, доц.
Фещур Р.В., канд. фіз.-мат. наук, проф.
I. ЗАГАЛЬНІ ПОЛОЖЕННЯ
Статистика як наука вивчає кількісну сторону різноманітних економічних і соціальних явищ, процесів суспільного життя з урахуванням їх якісної сторони. Метою вивчення дисципліни є опанування студентами методологією аналізу та обробки статистичної інформації та методологією розрахунку основних економічних показників, що відображають діяльність окремих підприємств та галузей економіки України.
Дані методичні вказівки розроблені для виконання студентами програми лабораторних робіт з дисципліни «Статистика». Лабораторні роботи призначені для набуття знань та розвитку вмінь студентів проводити статистичні дослідження. Перед студентами ставиться завдання навчитись:
- впорядковувати первинний статистичний матеріал;
- обирати метод аналізу відповідно до мети дослідження;
- здійснювати обробку та аналіз статистичних даних;
- графічно представляти дані, отримані в результаті досліджень;
- формулювати висновки та практичні рекомендації за результатами проведеного аналізу.
Перелік лабораторних робіт охоплює весь курс дисципліни «Статистика». В результаті виконання лабораторних робіт студенти отримають необхідні знання та практичні навики для виконання наступних завдань статистичного дослідження:
- проведення систематизації та групування первинних даних;
- розрахунок узагальнюючих показників статистичної сукупності у формі відносних і середніх величин;
- аналіз варіації сукупності даних за допомогою відповідних статистичних показників;
- проведення вибіркового обстеження;
- вивчення взаємозв’язків між різними статистичними сукупностями;
- дослідження динаміки розвитку явищ.
Важливе завдання проведення лабораторних робіт зі статистики полягає в тому, щоб навчити студентів працювати із комп’ютерними засобами, зокрема застосовувати відповідні пакети стандартних прикладних програм. До даних методичних рекомендацій розроблено електронні додатки в середовищі MS Excel, які суттєво спрощують процес обробки інформації і представлення отриманих результатів.
Лабораторна робота № 1
Зведення та групування статистичних даних
Завдання 1. Метод простого групування статистичних даних
Мета завдання: Навчитися систематизувати первинну інформацію, використовуючи зведення та метод простого групування статистичних даних.
Зміст завдання: У відповідності із варіантом завдання утворити ряди розподілу робітників підприємства:
a) за віком;
b) за величиною загального робочого стажу;
c) за неперервним стажем роботи на даному підприємстві;
d) за кваліфікаційним розрядом;
e) за розміром заробітної плати.
Таблиця 1.1
Вибір варіантів завдання
| Перша літера прізвища студента | А-Е | Є-Й | К-П | Р-Х | Ц-Я |
| Номери завдань, які необхідно виконати | a | b | c | d | e |
&
Отримані в результаті статистичного спостереження дані потребують упорядкування, систематизації та наукової обробки. З цією метою здійснюють їх зведення – загальне упорядкування даних, підрахунок кількості обстежених одиниць сукупності у відповідності із завданням аналізу.
Подальше групування статистичних даних передбачає розподіл статистичної сукупності на групи за однією або більше ознаками. В результаті здійснюється певна узагальнена оцінка одиниць сукупності та їх систематизація. Групування за однією ознакою називають простим групуванням.
Як привило, при групуванні за кількісною ознакою постає питання щодо кількості груп. Якщо досліджувана ознака має невелику кількість варіантів, то кількість груп визначається за принципом зручності, наприклад, груп може бути стільки, скільки існує варіантів досліджуваної ознаки. В такому випадку переважно формується дискретний ряд розподілу – ряд, в якому досліджувані ознаки виражені окремим цілим числом.
Якщо досліджувана ознака характеризується великою кількістю варіантів, то кількість груп доцільно визначати за формулою Стерджеса:
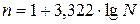 (1.1)
(1.1)
де N – кількість одиниць сукупності.
При цьому формується інтервальний ряд розподілу із представленням групувальної ознаки у вигляді інтервалу. Величина інтервалу визначається за формулою:
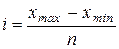 (1.2)
(1.2)
де x max і x min – відповідно найбільше і найменше значення ознаки.
В загальному випадку, ряд розподілу – це впорядкований розподіл одиниць статистичної сукупності за групувальною ознакою. Він складається із варіантів (значень групувальної ознаки) і частот (числа, що показують скільки разів повторюються окремі значення групувальної ознаки). Накопичену частоту називають кумулятивною частотою.
Графічно дискретний ряд розподілу зображується у вигляді полігону, інтервальний ряд розподілу можна зображати як у вигляді гістограми, так і у вигляді полігону (при цьому точками з’єднань є середини інтервалів). Накопичену частоту графічно зображають у вигляді кумуляти.
Послідовність виконання завдання:
1. Використовуючи первинні дані індивідуального завдання сформувати вихідну таблицю статистичних даних для характеристики робітників підприємства за заданою ознакою.
Таблиця 1.2
Вихідна таблиця статистичних даних
| № з/п | Назва ознаки | № з/п | Назва ознаки | № з/п | Назва ознаки |
| 1 | 54 | 107 | |||
| 2 | 55 | 108 | |||
| … | … | … | |||
| 53 | 106 | 159 |
2. Сформувати таблицю впорядкованих даних для характеристики робітників підприємства за заданою ознакою. Для цього потрібно впорядкувати статистичні дані за зростанням досліджуваної ознаки. Результати представити в табл. 1.3.
Таблиця 1.3
Таблиця впорядкованих даних
| Назва ознаки | № з/п | Назва ознаки | № з/п | Назва ознаки | № з/п |
| … | … | … | |||
| … | … | … |
3. Побудувати інтервальний (дискретний) ряд розподілу робітників підприємства за досліджуваною ознакою. Для цього потрібно:
- розрахувати кількість груп та величину інтервалу групування;
- провести підрахунок кількості робітників у кожному інтервалі групування та їх загальну кількість;
- провести підрахунок накопиченої кількості робітників підприємства.
Результати переставити в табл. 1.4.
Таблиця 1.4
Вибір варіантів завдання
| Перша літера прізвища студента | А-Е | Є-Й | К-П | Р-Х | Ц-Я |
| Номери завдань, які необхідно виконати | b | c | a | d | e |
&
При вирішенні завдань групування за декількома ознаками використовують комбінаційне групування. При комбінаційному групуванні сукупність поділяють спочатку за однією ознакою, а потім всередині кожної групи – за іншою. Так можна групувати за двома, трьома ознаками або й більшою їх кількістю.
Принципи розрахунку кількості груп при комбінаційному групуванні аналогічні до принципів простого групування.
Комбінаційні групування відграють особливу роль у тих випадках, коли досліджуються складні економічні явища. В такій ситуаціях одночасне використання декількох групувальних ознак, взятих у поєднанні одна з одною, дозволяє більш повно та всебічно охарактеризувати досліджуване явище, ніж використання окремих простих групувань.
Послідовність виконання завдання:
1. Використовуючи первинні дані індивідуального завдання сформувати вихідну таблицю статистичних даних для характеристики робітників підприємства за заданими ознаками.
Таблиця 1.6
Вихідна таблиця статистичних даних
| № з/п | Назва ознаки 1 | Назва ознаки 2 | № з/п | Назва ознаки 1 | Назва ознаки 2 | № з/п | Назва ознаки 1 | Назва ознаки 2 |
| 1 | 54 | 107 | ||||||
| 2 | 55 | 108 | ||||||
| … | … | … | ||||||
| 53 | 106 | 159 |
2. Сформувати таблицю впорядкованих даних для характеристики робітників підприємства за заданими ознаками. Для цього потрібно впорядкувати статистичні дані за зростанням першої досліджуваної ознаки. Результати представити в табл. 1.7.
Таблиця 1.7
Таблиця впорядкованих даних
| Назва ознаки 1 | Назва ознаки 2 | № з/п | Назва ознаки 1 | Назва ознаки 2 | № з/п | Назва ознаки 1 | Назва ознаки 2 | № з/п |
| … | … | … | ||||||
| … | … | … | ||||||
| … | … | … |
3. Побудувати інтервальний (дискретний) ряд розподілу робітників підприємства за досліджуваними двома ознаками використовуючи метод комбінаційного розподілу. Для цього потрібно:
- розрахувати кількість груп та величину інтервалів групування за ознакою 1;
- розрахувати кількість груп та величину інтервалів групування за ознакою 2;
- провести підрахунок кількості робітників у кожному інтервалі групування та їх загальну кількість.
Результати переставити у вигляді табл. 1.8.
Таблиця 1.8
Вибір варіантів завдання
| Перша літера прізвища студента | А-Е | Є-Й | К-П | Р-Х | Ц-Я |
| Номери завдань, які необхідно виконати | d, e | a, f | b, e | c, f | a, e |
&
Різні види групувань використовуються для розв’язання різних завдань статистичного дослідження. Розрізняють типологічне, структурне та аналітичне групування.
За допомогою типологічного групування виділяються найхарактерніші групи, типи явищ з яких складається неоднорідна статистична сукупність. Наприклад, групування населення за демографічними ознаками такими, як стать, рівень освіти та інше; розподіл підприємства за формою власності, за галузевою належністю тощо.
Структурними називаються групування, які дають характеристику розподілу однорідної сукупності за певними ознаками та показують співвідношення між окремими групами. Прикладом такого групування є розподіл населення за віком, розподіл робітників за стажем роботи, розподіл підприємств за рівнем доходів.
Аналітичне групування використовується для виявлення існування та напряму зв’язку між ознаками, які покладені в основу групування. При цьому одну із групувальних ознак розглядають як групувальну, а іншу як факторну.
Зв’язок між досліджуваними ознаками можна виявити і оцінити, визначивши у кожній групі, сформованій за факторною ознакою, середнє значення результативної ознаки. При існуванні зв’язку між факторною і результативною ознаками групові середні результативної ознаки послідовно змінюються (збільшуються чи зменшуються) від групи до групи.
Послідовність виконання завдання:
1. У відповідності із варіантом завдання визначити досліджувані факторну і результативну ознаки.
2. Використовуючи первинні дані індивідуального завдання сформувати вихідну таблицю статистичних даних для характеристики робітників підприємства за заданими ознаками.
Таблиця 1.10
Вихідна таблиця статистичних даних
| № з/п | Назва факторної ознаки | Назва результативної ознаки | № з/п | Назва факторної ознаки | Назва результативної ознаки | № з/п | Назва факторної ознаки | Назва результативної ознаки |
| 1 | 54 | 107 | ||||||
| 2 | 55 | 108 | ||||||
| … | … | … | ||||||
| 53 | 106 | 159 |
3. Сформувати таблицю впорядкованих даних для характеристики робітників підприємства за заданими ознаками. Для цього потрібно впорядкувати статистичні дані за зростанням факторної ознаки. Результати представити в табл. 1.11.
Таблиця 1.11
Таблиця впорядкованих даних
| Назва факторної ознаки | Назва результативної ознаки | № з/п | Назва факторної ознаки | Назва результативної ознаки | № з/п | Назва факторної ознаки | Назва результативної ознаки | № з/п |
| … | … | … | ||||||
| … | … | … | ||||||
| … | … | … |
4. Сформувати інтервальний (дискретний) ряд розподілу робітників за факторною ознакою. Для цього потрібно:
- провести розрахунок кількості груп та величини інтервалів групування;
- обчислити сумарне значення результативної ознаки та середнє значення результативної ознаки у кожному інтервалі.
Результати розрахунків представити у вигляді таблиці 1.12.
Таблиця 1.12
Лабораторна робота № 2
Структура посівних площ
| Назва області | Загальна земельна площа, тис. га | Вся посівна площа | В тому числі в % до посівної площі | ||||
| тис. га | у % до загальної площі | Зернові культури | Технічні культури | Картопля та овочево-баштанні культури | Кормові культури | ||
| Україна | |||||||
2. Визначити:
- питому вагу всієї посівної площі області у всій посівній площі України;
- визначити питому вагу площі, відведеної під зернові, технічні, картопляні і овочево-баштанні та кормові культури в даній області у площі, відведеній під цю культуру по Україні.
Результати подати у вигляді таблиці 2.2.
Таблиця 2.2
Порівняльний аналіз площ,
Лабораторна робота № 3
Аналіз статистичних даних
Лабораторна робота № 4
Вибір варіантів завдання
| Перша літера прізвища студента | А - Е | Є - Й | К - П | Р - Х | Ц - Я |
| Номери завдань, які необхідно виконати | d | e | a | b | c |
&
Вибіркове спостереження – це такий вид несуцільного спостереження, при якому отримують характеристику всієї сукупності одиниць на осевої дослідження деякої її частини. Вибіркове спостереження отримало широке практичне застосування завдяки своїм численним перевагам перед суцільним.
В теорії вибіркового спостереження розрізняють поняття генеральної та вибіркової сукупностей. Сукупність, з якої відбираються елементи для обстеження називається генеральною, а сукупність, яку безпосередньо обстежують – вибірковою. Оскільки вибіркова сукупність не точно відтворює структуру генеральної, то вибіркові оцінки певним чином відрізняються від характеристик генеральної сукупності. Розбіжності між ними називаються похибками репрезентативності.
Формування репрезентативної вибірки (тобто такої, що правильно характеризує генеральну сукупність) здійснюється за певними правилами. Використовують різні способи формування вибіркових сукупностей, зокрема випадковий, механічний, типовий та серійний.
Випадковий відбір ґрунтується на принципі випадковості визначення елементів, що увійдуть у вибіркову сукупність. При механічному способі формування відбір елементів вибірки проводиться механічно, через певний інтервал. Типовий відбір передбачає попередню структуризацію генеральної сукупності на однотипні складові частини та незалежний відбір елементів у кожній із них. При серійному відборі вибірка формується із серій елементів сукупності, які певним чином між собою пов’язані.
За схемою відбору елементів вибіркова сукупність буває безповторною (кожен елемент може попасти у вибірку тільки один раз) і повторною (елемент може попасти у вибірку більше, ніж один раз).
Початковим завданням при проведенні вибіркового дослідження є визначення обсягу вибірки, тобто кількості елементів, які увійдуть у вибіркову сукупність. Обсяг вибірки визначається при:
| безповторному відборі | повторному відборі |
|
|
|
| (4.1) |
де N – обсяг генеральної сукупності;
Δx – гранична похибка вибірки для заданої ймовірності Р;
t – довірче число (коефіцієнт довіри) для заданого значення ймовірності Р (визначається на основі табличних даних Додатку В);
σ – середнє квадратичне відхилення, яке обчислюється з використанням формули наближеного розрахунку (σ ≈ ( x max - x min )/6 ).
Для формування вибіркової сукупності способом механічного відбору потрібно визначити крок відбору за формулою і = N/n.
Для формування вибіркової сукупності способом простого випадкового повторного відбору доцільно скористатись можливостями програмного пакету Excel. Введення формули = INT(RAND()*158+1) (англомовна версія) або =ЦЕЛОЕ(СЛЧИС()*158+1) (російськомовна версія) дозволяє отримати у вільній комірці випадкове число в діапазоні від 1 до 159 значень, відповідно до кількості одиниць генеральної сукупності. Якщо протягнути за допомогою лівої клавіші мишки формулу донизу на кількість комірок, що відповідають величні обсягу вибірки, то отримаємо випадковий набір порядкових номерів робітників для формування вибірки. Для зручності доцільно скопіювати значення чисел даної послідовності у вільні комірки (це дозволить уникнути постійного оновлення даних).
Для формування вибіркових сукупностей методом простого випадкового і механічного відборів можна також скористатись інструментом Вибірка (Sampling). Інструмент Вибірка є елементом надбудови Аналіз даних (Data Analysis) і розміщується в меню Сервіс (Tools). Якщо ця надбудова відсутня в меню Сервіс (Tools), виберіть команду Надбудови (Add-Ins) і вкажіть Аналіз даних (Data Analysis) в списку надбудов, та добавте цей компонент.)
Середнє вибіркової сукупності обчислюється за формулою:
|
| (4.2) |
Результат проведеного вибіркового спостереження записується у вигляді довірчого інтервалу, що є інтервальною оцінкою параметрів генеральної сукупності:
|
| (4.3) |
Очевидно, що чим менший довірчий інтервал, тим точнішою є оцінка.
Для порівняння отриманих результатів із показниками генеральної сукупності доцільно визначити абсолютну і відносну похибки вибірок.
Абсолютна похибка вибірки обчислюється за формулою:
|
| (4.4) |
де 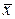 - середнє генеральної сукупності, обчислюється за формулою:
- середнє генеральної сукупності, обчислюється за формулою:
|
| (4.5) |
Відносна похибка вибірки обчислюється за формулою:
|
| (4.6) |
Порівняння похибок для двох способів відбору дозволить зробити висновок про відносну точність отриманих за їх допомогою результатів дослідження. З двох, використаних в даній лабораторній роботі способів формування вибіркової сукупності кращі результати дає той спосіб, для якого характерною є менша величина похибок.
Послідовність виконання завдання:
1. Використовуючи первинні дані індивідуального завдання представити генеральну сукупність статистичних даних у вигляді таблиці 4.2.
Таблиця 4.2
Генеральна сукупність даних для дослідження (вказати назву ознаки)
| № з/п | Назва ознаки | № з/п | Назва ознаки | № з/п | Назва ознаки |
| 1 | 54 | 107 | |||
| 2 | 55 | 108 | |||
| … | … | … | |||
| … | … | … | |||
| 52 | 105 | 158 | |||
| 53 | 106 | 159 |
2. Визначити обсяг вибірки для проведення вибіркового статистичного дослідження.
3. Сформувати вибіркову сукупність 2 способами:
- способом механічного відбору;
- способом простого випадкового повторного відбору.
Представити сформовані вибіркові сукупності статистичних даних у вигляді таблиці 4.3.
Таблиця 4.3
Вибіркова сукупність даних сформована способом (вказати назву способу формування)
| № з/п | Назва ознаки | № з/п | Назва ознаки | № з/п | Назва ознаки |
| … | … | … | |||
| … | … | … | |||
| … | … | … |
4. Для кожної із отриманих вибіркових сукупностей визначити:
- середнє значення досліджуваної ознаки;
- довірчий інтервал вибірки;
- абсолютну і відносну похибки вибірки.
5. За результатами дослідження зробити висновки про точність використаних методів вибіркового спостереження.
GКонтрольні питання
1. Що таке вибіркове спостереження? Які його переваги у порівнянні із суцільним спостереженням?
2. Що таке генеральна сукупність? Що таке вибіркова сукупність?
3. Чому виникають похибки репрезентативності?
4. Як визначається обсяг вибірки?
5. Яким чином формується вибіркова сукупність способом механічного відбору?
6. Яким чином формується вибіркова сукупність способом випадкового відбору?
7. Як обчислюється середнє вибіркової сукупності?
8. Що характеризує довірчий інтервал?
9. Для чого і як розраховуються абсолютна і відносна похибки вибірки?
10. Який із двох способів формування вибірки в даній лабораторній роботі дає точніші результати?
Вибір варіантів завдання
| Перша літера прізвища студента | А - Е | Є - Й | К - П | Р - Х | Ц - Я |
| Номери завдань, які необхідно виконати | c | b | e | d | a |
&
Основними завданнями проведення вибіркового спостереження є визначення середнього розміру досліджуваної ознаки (див. завдання 1 лабораторної роботи № 4) та визначення частки досліджуваної ознаки у певній сукупності.
При здійсненні вибіркового спостереження для визначення частки досліджуваної ознаки актуальними є всі теоретичні положення, описані у завданні 1 лабораторній роботі № 4. Обсяг вибірки визначається при
| безповторному відборі: | повторному відборі: |
|
|
|
| (4.7) |
де N – обсяг генеральної сукупності;
Δx – гранична похибка вибірки для заданої ймовірності Р;
t – довірче число (коефіцієнт довіри) для заданого значення ймовірності Р (визначається на основі табличних даних Додатку В);
p – частка одиниць сукупності, які мають певні значення ознаки (p = M/N, де M – кількість одиниць, які мають певні значення ознаки);
(1- p ) – частка одиниць сукупності із протилежним значенням ознаки;
p (1- p ) – дисперсія частки, значення якої можна розрахувати за результатами завдання 1 лабораторної роботи № 1.
Для формування вибіркової сукупності способом простого випадкового безповторного відбору доцільно скористатись можливостями програмного пакету Excel (див. завдання 1 лабораторної роботи № 4.)
Частка вибіркової сукупності обчислюється за формулою:
|
| (4.8) |
де m – кількість одиниць, які мають певні значення ознаки
Результат проведеного вибіркового спостереження записується у вигляді довірчого інтервалу:
|
| (4.9) |
Для порівняння отриманих результатів із показниками генеральної сукупності доцільно визначити абсолютну і відносну похибки вибірок.
Абсолютна похибка вибірки обчислюється за формулою:
|
| (4.10) |
де p - частка ознаки генеральної сукупності (p = M/N, де M – кількість одиниць, які мають певні значення ознаки), w – частка ознаки вибіркової сукупності.
Відносна похибка вибірки обчислюється за формулою:
|
| (4.11) |
Порівняння обчисленої відносної похибки із її граничним значенням дозволяє зробити висновок про точність проведеного вибіркового спостереження: якщо відносна похибка менша за її граничне значення, то точність спостереження є задовільною і отримані результати дозоляють характеризувати досліджувані параметри генеральної сукупності.
Послідовність виконання завдання:
1. Використовуючи первинні дані індивідуального завдання представити генеральну сукупність статистичних даних у вигляді таблиці 4.5.
Таблиця 4.5
Генеральна сукупність даних для дослідження (вказати назву ознаки)
| № з/п | Назва ознаки | № з/п | Назва ознаки | № з/п | Назва ознаки |
| 1 | 54 | 107 | |||
| 2 | 55 | 108 | |||
| … | … | … | |||
| … | … | … | |||
| 52 | 105 | 158 | |||
| 53 | 106 | 159 |
2. Визначити обсяг вибірки для проведення вибіркового статистичного дослідження.
3. Сформувати вибіркову сукупність способом простого випадкового безповторного відбору. Представити сформовані вибіркову сукупність у вигляді таблиці 4.6.
Таблиця 4.6
Лабораторна робота № 5
Вибір варіантів завдання
| Перша літера прізвища студента | А - Е | Є - Й | К - П | Р - Х | Ц - Я |
| Номери завдань, які необхідно виконати | c | b | d | a | f |
&
Одним із найважливіших завдань статистики є дослідження характеру взаємозв’язків між різними соціально-економічними явищами, що мають причинно-наслідковий характер. Ознаки, що характеризують причини та умови зв’язку, називають факторними ознаками ”x”, а ті, що характеризують наслідки – результативними ознаками ”y”. Між ознаками x та y виникають різні за природою та характером зв’язки, зокрема функціональні та стохастичні. При функціональному зв’язку кожному значенню ознаки х відповідає одне чітко визначене значення ознаки у. При стохастичному зв’язку кожному значенню ознаки х відповідає певна множина значень у, які утворюють так званий умовний розподіл. Вивчення стохастичних зв’язків є досить складним завданням, тому в статистичних дослідженнях, як правило, замінюють умовний розподіл середньою величиною 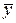 , в результаті чого утворюється різновид стохастичного зв’язку – кореляційний зв’язок.
, в результаті чого утворюється різновид стохастичного зв’язку – кореляційний зв’язок.
Одним із методів дослідження кореляційного зв’язку є кореляційно-регресійний аналіз. У цій моделі аналізу кореляційний зв’язок задається теоретичною лінією регресії (рівнянням). Рівняння регресії – це аналітична функція, яка описує залежність результативної ознаки від факторної. При виборі форми рівняння регресії важливим є якісний аналіз досліджуваних явищ.
Найпоширенішою та найпростішою в статистичному аналізі формою рівняння регресії є лінійна однофакторна функція Y = a + bx. Параметр b – коефіцієнт регресії вказує на скільки одиниць в середньому зміниться у із зміною х на одиницю. Він має одиницю виміру результативної ознаки. Параметр a називають вільним членом рівняння регресії, тобто це значення у при х = 0. Якщо х не набуває нульових значень, цей параметр має лише розрахункове призначення.
Знаходження параметрів рівняння регресії базується на методі найменших квадратів. Параметри a і b лінійного однофакторного рівняння визначаються із системи нормальних рівнянь, яка для не згрупованих даних записується як:
|
| (5.1) |
Якщо дані згруповані, наприклад, представлені у вигляді аналітичного групування, то система нормальних рівнянь має наступний вигляд:
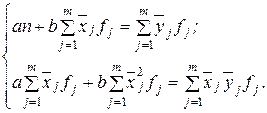 (5.2)
(5.2)
Тобто при побудові системи нормальних рівнянь за згрупованими даними застосовуються зважені з допомогою частот суми значень ознак, їх квадратів і добутків.
Щільність кореляційного зв’язку оцінюють за допомогою коефіцієнта детермінації R2, який розраховується за формулою:
|
| (5.3) |
де 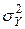 – дисперсія теоретичних значень, яку ще називають факторною і обчислюють
– дисперсія теоретичних значень, яку ще називають факторною і обчислюють
- для не згрупованих даних 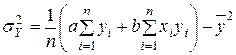 ;
;
- для згрупованих даних як 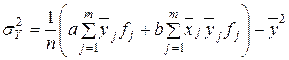 ;
;
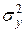 – загальна дисперсія.
– загальна дисперсія.
R2 змінюється від 0 до 1 і показує, яка частина загальної варіації результативної ознаки зумовлена факторною ознакою, а яка – зумовлена іншими факторами, не врахованими при побудові рівнянні регресії. При R2 = 1 рівняння регресії проходить через усі емпіричні точки і встановлює точну відповідність між значеннями ознаки х і значеннями ознаки у. Тобто у цьому випадку між ознаками х та у існує функціональний зв’язок. R2 = 0 є свідченням відсутності зв’язку, вираженого даним рівнянням регресії. При використанні коефіцієнта детермінації слід враховувати, що дисперсія теоретичних значень 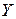 характеризує не всю варіацію результативної ознаки у, пов’язану з варіацією факторної ознаки х, а лише ту її частину, яка відповідає теоретичному рівнянню регресії. Тому коефіцієнт детермінації в кореляційно-регресійному аналізі є фактично показником якості апроксимації вибраною теоретичною лінією регресії кореляційного зв’язку між ознаками.
характеризує не всю варіацію результативної ознаки у, пов’язану з варіацією факторної ознаки х, а лише ту її частину, яка відповідає теоретичному рівнянню регресії. Тому коефіцієнт детермінації в кореляційно-регресійному аналізі є фактично показником якості апроксимації вибраною теоретичною лінією регресії кореляційного зв’язку між ознаками.
Для дослідження лінійного зв’язку використовують також лінійний коефіцієнт кореляції (Пірсона), який доцільно обчислювати за формулою:
|
| (5.4) |
Цей коефіцієнт змінюється від -1 до +1 і дозволяє оцінити як щільність кореляційного зв’язку, так і його напрям. Напрям визначається знаком коефіцієнта кореляції Пірсона (”+” – прямий, ”-” – обернений). При |r = 1| існує лінійна функціональна залежність, при r = 0 – зв’язок відсутній. Чим ближчий r за своїм абсолютним значенням до 1, тим вища щільність зв’язку, чим ближчий до 0, тим вона нижча.
Грубою помилкою є розрахунок коефіцієнта кореляції між середніми значеннями факторної і результативної ознак, представленими в аналітичній груповій таблиці. Як правило, величина лінійного коефіцієнта кореляції, розрахованого таким чином, близька до одиниці, тоді як дійсна степінь щільності і зв’язку може бути значно нижчою.
Перевірка істотності зв’язку здійснюється шляхом порівняння фактичного значення R2 з його критичним значенням R21-α (k1,k2) (визначається за таблицями з додатку Д). k1 і k2 – ступені вільності, які обчислюються наступним чином:
| k1 = m – 1 і k2 = n – m | (5.5) |
де m – кількість параметрів теоретичного рівняння регресії, n – кількість елементів сукупності.
Якщо фактичне значення R2 більше за критичне, то зв’язок між результативною та факторною ознакою вважається істотним. Якщо фактичне значення R2 менше, ніж критичне, то наявність кореляційного зв’язку між ознаками не доказана і зв’язок вважається неістотним.
Перевірку істотності зв’язку з використанням F-критерію (критерію Фішера) проводять шляхом порівняння фактичного значення F-критерію з його критичним (табличним) значенням. Фактичне значення F-критерію розраховується за формулою:
|
| (5.6) |
Критичне значення позначається F1-α( k1; k2) і визначається на основі таблиці Додатку Г. Якщо фактичне значення F-критерію більше за критичне, то це свідчить про істотність зв’язку. Якщо ж фактичне значення F-критерію менше за критичне, то істотність зв’язку не доведена.
На рис. 5.1 представлений приклад графічного зображення теоретичної лінії регресії та емпіричних даних, що відображають зв’язок між витратами підприємства на рекламу та його доходами.
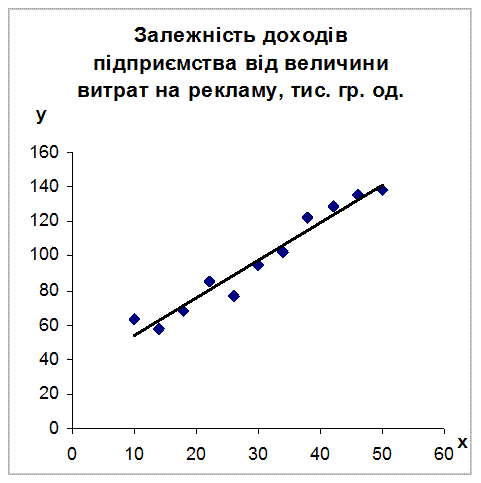
Рис. 5.1. Приклад графічного зображення теоретичної лінії регресії та емпіричних даних
Послідовність виконання завдання:
1. Відповідно до індивідуального завдання для двох заданих ознак побудувати вихідну таблицю статистичних даних у вигляді таблиці 5.2.
Таблиця 5.2
Вихідна таблиця статистичних даних
| № з/п | Назва факторної ознаки | Назва результативної ознаки | № з/п | Назва факторної ознаки | Назва результативної ознаки | № з/п | Назва факторної ознаки | Назва результативної ознаки |
| 1 | 54 | 107 | ||||||
| 2 | 55 | 108 | ||||||
| … | … | … | ||||||
| … | … | … | ||||||
| 52 | 105 | 158 | ||||||
| 53 | 106 | 159 | ||||||
2. Сформувати таблицю впорядкованих даних, результати представити в табл. 5.3.
Таблиця 5.3
Таблиця впорядкованих даних
| Назва факторної ознаки | Назва результативної ознаки | № з/п | Назва факторної ознаки | Назва результативної ознаки | № з/п | Назва факторної ознаки | Назва результативної ознаки | № з/п |
| … | … | … | ||||||
| … | … | … | ||||||
| … | … | … |
2. Провести аналітичне групування статистичних даних, результати якого представити у вигляді таблиці 5.4.
Таблиця 5.4
Аналітичне групування для дослідження кореляційного зв’язку між ознаками (вказати назви ознак)
| № з/п | Інтервали за факторною ознакою, xj | Середина інтервалу
| Кількість робітників, f j | Середнє значення результативної ознаки, | Допоміжні розрахункові параметри | ||
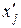 f j f j
| 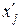 2 f j 2 f j
| 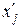 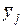 f j f j
| |||||
| ………………. | |||||||
| Сумарні значення | |||||||
| Середні значення | |||||||
3. Обчислити параметри рівняння регресії, яке відображає залежність між факторною та результативною ознаками. Записати вид отриманого рівняння регресії.
4. За допомогою коефіцієнта детермінації оцінити щільність кореляційного зв’язку.
5 Перевірити істотність зв’язку за допомогою критичних значень коефіцієнта детермінації R2 та F-критерію (критерію Фішера) при α = 0,05.
6. Зобразити графічно теоретичну лінію регресії та емпіричні дані у вигляді точок.
7. За результатами дослідження зробити висновки про взаємозв’язок між досліджуваними ознаками.
GКонтрольні питання
1. Які ознаки називаються факторними? Які ознаки називаються результативними?
2. Які особливості функціонального та стохастичного зв’язку?
3. Який зв’язок називається кореляційним?
4. Що таке рівняння регресії?
5. Для чого використовується коефіцієнт детермінації? Який діапазон його значень?
6. В чому полягають особливості використання та суть лінійного коефіцієнта кореляції?
7. Як здійснюється перевірка істотності зв’язку з використанням F-критерію?
Вибір варіантів завдання
| Перша літера прізвища студента | А - Е | Є - Й | К - П | Р - Х | Ц - Я |
| Номери завдань, які необхідно виконати | b | c | a | d | e |
&
Дисперсійний аналіз – це один із методів дослідження взаємозв’язків між явищами у статистиці. Суть його полягає в тому, що спочатку всі елементи сукупності групують за факторною ознакою х і в кожній групі обчислюють середні значення результативної ознаки у. Подальша оцінка щільності зв’язку при дисперсійному аналіз ґрунтується на правилі складання дисперсій. Для цього потрібно розрахувати наступні види дисперсій: внутрішньогрупову, середню з внутрішньогрупових, міжгрупову та загальну дисперсії результативної ознаки.
Внутрішньогрупова дисперсія – це середній квадрат відхилень значень результативної ознаки у від групової середньої 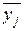 . Вона розраховується окремо для кожної j-ї групи, сформованої за факторною ознакою х:
. Вона розраховується окремо для кожної j-ї групи, сформованої за факторною ознакою х:
|
| (5.6) |
Ця варіація показує вплив умов, що діють в середні групи. Оскільки одиниці сукупності, які об’єднуються в групи, певною мірою схожі, то варіація в групах, як правило, менша, ніж варіація в сукупності в цілому.
Середня із внутрішньогрупових дисперсій є узагальнюючою мірою варіації в середині груп, виділених за факторною ознакою. Вона обчислюється за формулою:
|
| (5.7) |
Міжгрупова дисперсія – це середній квадрат відхилень групових середніх від загальної середньої. Вона характеризує варіацію між групами, виділеними за факторною ознакою. Чим більша різниця між групами, тим більше значення цього показника. Формула розрахунку наступна:
|
| (5.8) |
де 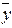 – загальна середня варіюючої результативної ознаки.
– загальна середня варіюючої результативної ознаки.
Загальна дисперсія характеризує варіацію значень ознаки навколо загальної середньої, тобто є загальною характеристикою варіації у сукупності.
Згідно правила складання дисперсій загальну дисперсію можна представити у вигляді суми міжгрупової та середньої з внутрішньогрупових дисперсій:
|
| (5.9) |
Отже, загальна дисперсія характеризує варіацію ознаки y за рахунок впливу всіх факторів, міжгрупова – за рахунок фактору х, покладеного в основу групування, а внутрішньогрупові – за рахунок інших факторів, не врахованих у групуванні.
Мірою щільності зв’язку є відношення міжгрупової дисперсії до загальної, яке називають кореляційним відношенням:
|
| (5.10) |
Кореляційне відношення змінюється від 0 до 1 і показує, яка частина варіації результативної ознаки х залежить від варіації факторної ознаки х. Чим ближче значення η2 до 1, тим щільніший зв’язок, чим ближче η2 до 0, тим зв’язок слабший. Якщо η2 = 0, то зв’язок відсутній, якщо η2 = 1 – зв’язок функціональний.
Виконання умови η2 > 0 не є достатнім для твердження про існування кореляційного зв’язку між ознаками, оскільки деколи навіть при випадковому групуванні може виникнути зв’язок.
Перевірка істотності зв’язку відбувається шляхом порівняння фактичного значення η2 з його критичним значенням η21-α (k1,k2) (визначається за таблицями з Додатку Д). k1 і k2 – ступені вільності, які обчислюються наступним чином:
| k1 = m – 1 і k2 = n – m | (5.11) |
де m – кількість груп, n – кількість одиниць сукупності.
Якщо фактичне значення η2 більше за критичне, то зв’язок між результативною та факторною ознакою вважається істотним. Якщо фактичне значення η2 менше за критичне, то наявність кореляційного зв’язку між ознаками не доказана і зв’язок вважається неістотним.
Так само, перевірку істотності зв’язку з використанням F-критерію (критерію Фішера) проводять шляхом порівняння фактичного значення F-критерію з його критичним (табличним) значенням. Фактичне значення F-критерію розраховується за формулою:
|
| (5.12) |
Критичне значення позначається F1-α( k1; k2) і визначається на основі таблиці Додатку Г. Якщо фактичне значення F-критерію більше за критичне, то це свідчить про істотність зв’язку. Якщо ж фактичне значення F-критерію менше за критичне, то істотність зв’язку не доведена.
Послідовність виконання завдання:
1. Проведений у лабораторній роботі № 1 комбінаційний розподіл робітників підприємства за досліджуваними ознаками представити у вигляді таблиці 5.6.
Таблиця 5.6
Лабораторна робота № 6
Таблиця показників динаміки обсягу випуску продукції протягом 9 місяців
| t | Рівень ряду, y (t) | Абсолютний приріст | Темп зростання, % | Темп приросту, % | Абсолютне значення 1% приросту | ||||
| ланцюговий Δyi | базовий ΔyБi | ланцюговий Кi | базовий КБi | ланцюговий Тi | базовий ТБi | ланцюгове Тi | базове ТБi | ||
| 1 | |||||||||
| 2 | |||||||||
| ……. | |||||||||
| 9 | |||||||||
| Середнє значення | |||||||||
2. Провести згладжування за методом середніх плинних для трьох одиниць.
3. Спрогнозувати випуск продукції на десятий місяць.
4. Зобразити графічно емпіричний та згладжений ряди динаміки.
GКонтрольні питання
1. Що таке динаміка явища?
2. Що таке ряд динаміки? Які його складові?
3. Які показники використовуються для характеристики рядів динаміки?
4. Чим відрізняються ланцюгові показники динаміки від базисних?
5. Як розраховується абсолютний приріст?
6. Чим відрізняється коефіцієнт зростання від темпу зростання?
7. Як розраховується темп приросту?
8. В чому полягає зміст абсолютного значення 1 % приросту?
9. Для чого використовують середні значення показників динаміки?
10. Як відбувається згладжування ряду динаміки методом плинних середніх?
Лабораторна робота № 7
РЕКОМЕНДОВАНА ЛІТЕРАТУРА
1. Статистика: Підруч. / Герасименко С.С., Єріна А.М., Пальян З.О. – К.: КНЕУ, 2000. – 468 с.
2. Матковський С.О., Гальків Л.І., Гринькевич О.С., Сорочак О.З.. Статистика: Навчальний посібник – Львів: «Новий Світ – 2000», 2009. – 430 с.;
3. Тарасенко І.О. Статистика: Навчальний посібник. – К.: Центр навчальної літератури, 2006. – 344 с.
4. Статистика: Підручник / С.С.Герасименко, А.В.Головач, А.М.Єріна, О.В.Козирєв та ін.; За наук. ред. д.е.н. С.С.Герасименка – К.: Вища шк., 2000. – 467 с.
5. Статистика: теоретичні засади і прикладні аспекти. Навчальний посібник. Р.В.Фещур, А.Ф.Барвінський, В.П.Кічор та інші; За наук. ред. Р.В.Фещура. – 2-е вид. оновлене і доповнене. – Львів: «Інтелект-Захід», 2003. – 576 с.
6. Статистика. Збірник задач; Навч. Посібник /А.В.Головач, А.М.Єріна, О.В.Козирєв та ін. – К.: Вища шк., 1994. – 448 с.
7. Методичні вказівки для виконання лабораторних робіт з курсу «Статистика» для студентів Інституту економіки і менеджменту денної форми навчання. /Укладачі І.І.Новаківський, Я.В.Панас, О.Б.Стернюк – Львів: Видавництво НУ „ЛП” 2008. – 60 с.
НАВЧАЛЬНЕ ВИДАННЯ
СТАТИСТИКА
МЕТОДИЧНІ ВКАЗІВКИ
до виконання лабораторних робіт
для студентів напряму підготовки 6.030601 – „Менеджмент”
спеціальності „Менеджмент організацій і адміністрування”
Укладачі: Сорочак Олег Зіновійович,
Стернюк Оксана Богданівна,
Панас Ярослав Володимирович
МЕТОДИЧНІ ВКАЗІВКИ
до виконання лабораторних робіт
для студентів напряму підготовки 6.030601 – „Менеджмент”
спеціальності „Менеджмент організацій і адміністрування”
Затверджено
на засіданні кафедри
менеджменту організацій
Протокол № 9 від 11.03.2010 р.
Львів – 2010
Статистика: Методичні вказівки до виконання лабораторних робіт для студентів напряму підготовки 6.030601 – „Менеджмент” спеціальності „Менеджмент організацій і адміністрування” / Укл.: О.З.Сорочак, О.Б.Стернюк, Я.В.Панас. – Львів: Видавництво Національного університету „Львівська політехніка”, 2010. – 55 с.
Укладачі: Сорочак О.З., канд. техн. наук, доц.
Стернюк О.Б., асист.
Панас Я.В., асист.
Відповідальний за випуск: Чухрай Н.І., докт. екон. наук, проф.
Рецензенти: Войцеховська Ю.В., канд. екон. наук, доц.
Фещур Р.В., канд. фіз.-мат. наук, проф.
I. ЗАГАЛЬНІ ПОЛОЖЕННЯ
Статистика як наука вивчає кількісну сторону різноманітних економічних і соціальних явищ, процесів суспільного життя з урахуванням їх якісної сторони. Метою вивчення дисципліни є опанування студентами методологією аналізу та обробки статистичної інформації та методологією розрахунку основних економічних показників, що відображають діяльність окремих підприємств та галузей економіки України.
Дані методичні вказівки розроблені для виконання студентами програми лабораторних робіт з дисципліни «Статистика». Лабораторні роботи призначені для набуття знань та розвитку вмінь студентів проводити статистичні дослідження. Перед студентами ставиться завдання навчитись:
- впорядковувати первинний статистичний матеріал;
- обирати метод аналізу відповідно до мети дослідження;
- здійснювати обробку та аналіз статистичних даних;
- графічно представляти дані, отримані в результаті досліджень;
- формулювати висновки та практичні рекомендації за результатами проведеного аналізу.
Перелік лабораторних робіт охоплює весь курс дисципліни «Статистика». В результаті виконання лабораторних робіт студенти отримають необхідні знання та практичні навики для виконання наступних завдань статистичного дослідження:
- проведення систематизації та групування первинних даних;
- розрахунок узагальнюючих показників статистичної сукупності у формі відносних і середніх величин;
- аналіз варіації сукупності даних за допомогою відповідних статистичних показників;
- проведення вибіркового обстеження;
- вивчення взаємозв’язків між різними статистичними сукупностями;
- дослідження динаміки розвитку явищ.
Важливе завдання проведення лабораторних робіт зі статистики полягає в тому, щоб навчити студентів працювати із комп’ютерними засобами, зокрема застосовувати відповідні пакети стандартних прикладних програм. До даних методичних рекомендацій розроблено електронні додатки в середовищі MS Excel, які суттєво спрощують процес обробки інформації і представлення отриманих результатів.
Лабораторна робота № 1
Зведення та групування статистичних даних
Дата: 2019-03-05, просмотров: 576.
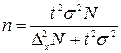
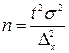
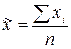
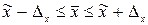
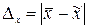
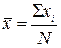
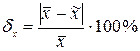
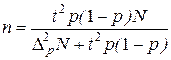
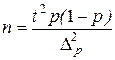
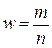
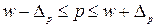
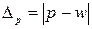
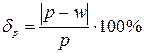
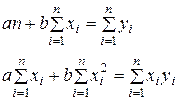
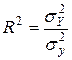 ,
,